Cauchy-Sequenz - Cauchy sequence
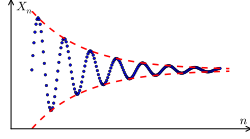
In der Mathematik , eine Cauchy - Sequenz ( Französisch Aussprache: [koʃi] ; Englisch: / k oʊ ʃ í / KOH -shee ), benannt nach Augustin-Louis Cauchy , ist eine Sequenz , deren Elemente beliebig nahe werden zueinander als die Sequenz schreitet voran. Genauer gesagt sind bei einem gegebenen kleinen positiven Abstand alle Elemente der Folge bis auf eine endliche Anzahl kleiner als der gegebene Abstand voneinander.
Es reicht nicht aus, dass jeder Begriff dem vorhergehenden Begriff beliebig nahe kommt . Zum Beispiel in der Folge der Quadratwurzeln natürlicher Zahlen:
Der Nutzen von Cauchy-Folgen liegt in der Tatsache, dass in einem vollständigen metrischen Raum (in dem alle diese Folgen bekanntermaßen gegen einen Grenzwert konvergieren ) das Konvergenzkriterium nur von den Termen der Folge selbst abhängt, im Gegensatz zur Definition von Konvergenz, die sowohl den Grenzwert als auch die Terme verwendet. Dies wird oft in Algorithmen , sowohl theoretischen als auch angewandten, ausgenutzt , bei denen relativ einfach ein iterativer Prozess gezeigt werden kann, um eine Cauchy-Folge zu erzeugen, die aus den Iterationen besteht und somit eine logische Bedingung wie die Termination erfüllt.
Verallgemeinerungen von Cauchy-Folgen in abstrakteren gleichförmigen Räumen existieren in Form von Cauchy-Filtern und Cauchy-Netzen .
In reellen Zahlen
Eine Sequenz
Für jede reelle Zahl r bildet die Folge abgeschnittener Dezimalentwicklungen von r eine Cauchy-Folge. Zum Beispiel, wenn diese Sequenz (3, 3.1, 3.14, 3.141, ...) ist. Die
m- ten und n- ten Terme unterscheiden sich höchstens, wenn m < n ist , und wenn m wächst, wird dies kleiner als jede feste positive ZahlModul der Cauchy-Konvergenz
Wenn eine Folge in der Menge ist, dann ist ein
Modul der Cauchy-Konvergenz für die Folge eine Funktion aus der Menge der natürlichen Zahlen zu sich selbst, so dass für alle natürlichen Zahlen und natürlichen ZahlenJede Folge mit einem Cauchy-Konvergenzmodul ist eine Cauchy-Folge. Die Existenz eines Modulus für eine Cauchy-Folge folgt aus der Wohlordnungseigenschaft der natürlichen Zahlen (sei die kleinstmögliche in der Definition der Cauchy-Folge, angenommen sei ). Die Existenz eines Modulus folgt auch aus dem Prinzip der
abhängigen Wahl , das eine schwache Form des Wahlaxioms ist, und es folgt auch aus einer noch schwächeren Bedingung namens AC 00 . Reguläre Cauchy-Folgen sind Folgen mit einem gegebenen Modul der Cauchy-Konvergenz (normalerweise oder ). Jede Cauchy-Folge mit einem Cauchy-Konvergenzmodul ist äquivalent zu einer regulären Cauchy-Folge; dies kann ohne irgendeine Form des Auswahlaxioms bewiesen werden.Die Moduli der Cauchy-Konvergenz werden von konstruktiven Mathematikern verwendet, die keine Form der Auswahl verwenden möchten. Die Verwendung eines Moduls der Cauchy-Konvergenz kann sowohl Definitionen als auch Sätze in der konstruktiven Analysis vereinfachen. Reguläre Cauchy-Sequenzen wurden von Errett Bishop in seinen Foundations of Constructive Analysis und von Douglas Bridges in einem nicht-konstruktiven Lehrbuch ( ISBN 978-0-387-98239-7 ) verwendet.
In einem metrischen Raum
Da die Definition einer Cauchy-Folge nur metrische Konzepte beinhaltet, ist es einfach, sie auf jeden metrischen Raum X zu verallgemeinern . Dazu wird der Absolutwert durch den Abstand (wobei
d eine Metrik bezeichnet ) zwischen und . ersetztFormal ist für einen metrischen Raum eine Folge
Grob gesagt rücken die Terme der Folge immer näher zusammen, was nahelegt, dass die Folge einen Grenzwert in X haben sollte . Nichtsdestotrotz existiert eine solche Grenze nicht immer innerhalb von X : Die Eigenschaft eines Raums, dass jede Cauchy-Folge im Raum konvergiert, wird Vollständigkeit genannt und wird weiter unten beschrieben.
Vollständigkeit
Ein metrischer Raum ( X , d ), in dem jede Cauchy-Folge gegen ein Element von X konvergiert, heißt vollständig .
Beispiele
Die reellen Zahlen sind vollständig unter der durch den üblichen Absolutwert induzierten Metrik, und eine der Standardkonstruktionen der reellen Zahlen beinhaltet Cauchy-Folgen von rationalen Zahlen . In dieser Konstruktion ist jede Äquivalenzklasse von Cauchy-Folgen rationaler Zahlen mit einem bestimmten Schwanzverhalten – also jede Klasse von Folgen, die sich beliebig nahe kommen – eine reelle Zahl.
Eine ziemlich andere Art von Beispiel bietet ein metrischer Raum X, der die diskrete Metrik hat (wo zwei beliebige Punkte im Abstand 1 voneinander sind). Jede Cauchy-Folge von Elementen von X muss über einen Fixpunkt hinaus konstant sein und konvergiert gegen den sich schließlich wiederholenden Term.
Nicht-Beispiel: rationale Zahlen
Die rationalen Zahlen sind nicht vollständig (für die übliche Entfernung): Es gibt Folgen von rationalen
Zahlen , die (in ) gegen irrationale Zahlen konvergieren ; dies sind Cauchy-Folgen ohne Begrenzung . Wenn eine reelle Zahl x irrational ist, dann ergibt die Folge ( x n ), deren n- ter Term die Kürzung auf n Dezimalstellen der Dezimalentwicklung von x ist , eine Cauchy-Folge rationaler Zahlen mit irrationaler Grenze x . Irrationale Zahlen gibt es zum Beispiel sicherlich in :- Die durch definierte Folge besteht aus rationalen Zahlen (1, 3/2, 17/12,...), was aus der Definition klar hervorgeht; es konvergiert jedoch gegen die
Nicht-Beispiel: offenes Intervall
Das offene Intervall in der Menge der reellen Zahlen mit einem normalen Abstand ist kein vollständiger Raum: gibt es eine Folge darin, die Cauchy (für beliebig kleine Distanz gebunden alle Bedingungen des Sitzes in dem Intervall), jedoch konvergiert nicht in — sein 'Limit', Nummer 0, gehört nicht zum Leerzeichen
Andere Eigenschaften
- Jede konvergente Folge (mit dem Grenzwert s , sagen wir) ist eine Cauchy-Folge, da bei einer gegebenen reellen Zahl jenseits eines Fixpunktes jeder Term der Folge innerhalb des Abstands von
Diese letzten beiden Eigenschaften liefern zusammen mit dem Satz von Bozen-Weierstrass einen Standardbeweis für die Vollständigkeit der reellen Zahlen, der eng mit dem Satz von Bozen-Weierstrass und dem Satz von Heine-Borel verwandt ist . Jede Cauchy-Folge reeller Zahlen ist beschränkt, hat also nach Bozen–Weierstrass eine konvergente Teilfolge, ist also selbst konvergent. Dieser Beweis der Vollständigkeit der reellen Zahlen verwendet implizit das Axiom der
kleinsten oberen Schranke . Der oben erwähnte alternative Ansatz, die reellen Zahlen als Vervollständigung der rationalen Zahlen zu konstruieren , macht die Vollständigkeit der reellen Zahlen tautologisch.Eine der üblichen Veranschaulichungen des Vorteils, mit Cauchy-Folgen arbeiten zu können und von der Vollständigkeit Gebrauch zu machen, liefert die Betrachtung der Summation einer unendlichen Reihe reeller Zahlen (oder allgemeiner von Elementen eines vollständigen normierten linearen Raums) . oder Banach-Raum ). Eine solche Reihe gilt genau dann als konvergent, wenn die Folge der
Teilsummen konvergent ist, wobei es routinemäßig zu bestimmen ist, ob die Folge der Teilsummen Cauchy ist oder nicht, da für positive ganze ZahlenWenn eine
gleichmäßig stetige Karte zwischen den metrischen Räumen M und N und ( x n ) in einer Cauchy - Sequenz M , dann ist eine Sequenz Cauchy in N . Sind und zwei Cauchy-Folgen in den rationalen, reellen oder komplexen Zahlen, dann sind auch Summe und Produkt Cauchy-Folgen.Verallgemeinerungen
In topologischen Vektorräumen
Es gibt auch ein Konzept der Cauchy-Folge für einen topologischen Vektorraum : Wähle eine
lokale Basis für ungefähr 0; dann ist ( ) eine Cauchy-Folge, wenn es für jedes Mitglied eine Zahl gibt, so dass jedes Mal , wenn ein Element von ist, wenn die Topologie von mit einer translationsinvarianten Metrik kompatibel ist, die beiden Definitionen übereinstimmen.In topologischen Gruppen
Da die topologische Vektorraumdefinition der Cauchy-Folge nur eine kontinuierliche "Subtraktions"-Operation erfordert, kann man sie genauso gut im Kontext einer topologischen Gruppe sagen : Eine Folge in einer topologischen Gruppe ist eine Cauchy-Folge, wenn für jede offene Umgebung der
Identität in gibt es eine Zahl, so dass, wenn wie oben folgt , es ausreicht, dies für die Umgebungen in einer beliebigen lokalen Basis der Identität in zu überprüfenWie bei der Konstruktion der Vervollständigung eines metrischen Raums kann man weiterhin die binäre Relation auf Cauchy-Folgen darin definieren und sind äquivalent, wenn für jede offene
Umgebung der Identität in eine Zahl existiert, so dass immer dann folgt, dass Diese Relation an Äquivalenzrelation : Sie ist reflexiv, da die Folgen Cauchy-Folgen sind. Es ist symmetrisch, da es durch Stetigkeit der Inversen eine weitere offene Umgebung der Identität ist. Es ist transitiv, da und wo offene Nachbarschaften der Identität sind, so dass ; solche Paare existieren durch die Kontinuität der Gruppenoperation.In Gruppen
Es gibt auch ein Konzept der Cauchy - Folge in einer Gruppe : Es wäre eine stetige Abnahme der seine
normalen Untergruppen von endlichem Index . Dann heißt eine Folge in Cauchy (bezüglich ) genau dann, wenn für any eine solche existiert, dass für alleTechnisch gesehen ist dies dasselbe wie eine topologische Gruppen-Cauchy-Folge für eine bestimmte Wahl der Topologie auf derjenigen, für die eine lokale Basis ist.
Die Menge solcher Cauchy-Folgen bildet eine Gruppe (für das komponentenweise Produkt), und die Menge der Nullfolgen (s.th. ) ist eine normale Untergruppe von Die
Faktorgruppe heißt die Vervollständigung von bzgl.Man kann dann zeigen, dass diese Vervollständigung isomorph zum inversen Limes der Folge ist
Ein in der Zahlentheorie und algebraischer Geometrie bekanntes Beispiel für diese Konstruktion ist die Konstruktion der
-adischen Vervollständigung der ganzen Zahlen bezüglich einer Primzahl In diesem Fall sind die ganzen Zahlen unter Addition, und ist die additive Untergruppe bestehend aus ganzzahligen Vielfachen vonWenn eine
kofinale Folge ist (d. h., jede Normaluntergruppe mit endlichem Index enthält einige ), dann ist diese Vervollständigung kanonisch in dem Sinne, dass sie isomorph zum inversen Grenzwert von where ist, der über alle Normaluntergruppen mit endlichem Index variiert . Für weitere Details siehe Kap. I.10 in Langs "Algebra".In einem hyperrealen Kontinuum
Eine reelle Folge hat eine natürliche
hyperreale Erweiterung, definiert für hypernatürliche Werte H des Indexes n zusätzlich zum üblichen natürlichen n . Die Folge ist Cauchy genau dann, wenn für jedes unendliche H und K die Werte und unendlich nah beieinander oder gleich sind , d.h.wobei "st" die Standardteilfunktion ist .
Cauchy Vervollständigung der Kategorien
Krause (2018) führte einen Begriff der Cauchy-Vervollständigung einer Kategorie ein . Angewandt auf (die Kategorie, deren Objekte rationale Zahlen sind, und es gibt genau dann einen Morphismus von
x nach y, wenn ), ergibt diese Cauchy-Vervollständigung (wiederum interpretiert als Kategorie unter Verwendung ihrer natürlichen Ordnung).Siehe auch
Verweise
Weiterlesen
- Bourbaki, Nicolas (1972). Kommutative Algebra (englische Übersetzung Hrsg.). Addison-Wesley. ISBN 0-201-00644-8.
- Krause, Henning (2018), Vollkommene Komplexe vervollständigen : Mit Anhängen von Tobias Barthel und Bernhard Keller , arXiv : 1805.10751 , Bibcode : 2018arXiv180510751B
- Lang, Serge (1993), Algebra (Dritte Aufl.), Reading, Mass.: Addison-Wesley, ISBN 978-0-201-55540-0, Zbl 0848.13001
- Spivak, Michael (1994). Kalkül (3. Aufl.). Berkeley, CA: Veröffentlichen oder zugrunde gehen. ISBN 0-914098-89-6. Archiviert vom Original am 17.05.2007 . Abgerufen am 26.05.2007 .
- Troelstra, AS ; D. van Dalen . Konstruktivismus in der Mathematik: Eine Einführung . (für Anwendungen in der konstruktiven Mathematik)
Externe Links
- "Grundlagenfolge" , Encyclopedia of Mathematics , EMS Press , 2001 [1994]