krummlinige Koordinaten - Curvilinear coordinates

krummlinige (oben), affine (rechts) und kartesische (links) Koordinaten im zweidimensionalen Raum

In der Geometrie sind krummlinige Koordinaten ein Koordinatensystem für den euklidischen Raum, in dem die Koordinatenlinien gekrümmt sein können. Diese Koordinaten können aus einem Satz kartesischer Koordinaten abgeleitet werden, indem eine Transformation verwendet wird, die lokal invertierbar ist (eine Eins-zu-Eins-Abbildung) an jedem Punkt. Dies bedeutet, dass man einen in einem kartesischen Koordinatensystem gegebenen Punkt in seine krummlinigen Koordinaten und zurück umwandeln kann. Der vom französischen Mathematiker Lamé geprägte Name krummlinige Koordinaten leitet sich von der Tatsache ab, dass die Koordinatenflächen der krummlinigen Systeme gekrümmt sind.

Bekannte Beispiele für krummlinige Koordinatensysteme im dreidimensionalen euklidischen Raum ( R ³ ) sind Zylinder- und Kugelkoordinaten . Eine kartesische Koordinatenfläche in diesem Raum ist eine Koordinatenebene ; beispielsweise Z = 0 definiert die x - y - Ebene. In dem gleichen Raum, koordiniert die Oberfläche r = 1 in sphärischen Koordinaten ist die Oberfläche einer Einheitskugel , die gekrümmt ist. Der Formalismus krummliniger Koordinaten liefert eine einheitliche und allgemeine Beschreibung der Standardkoordinatensysteme.

Krümmungskoordinaten werden oft verwendet, um den Ort oder die Verteilung physikalischer Größen zu definieren, die beispielsweise Skalare , Vektoren oder Tensoren sein können . Mathematische Ausdrücke, die diese Größen in der Vektorrechnung und Tensoranalyse verwenden (wie Gradient , Divergenz , curl und Laplace ) können gemäß den Transformationsregeln für Skalare, Vektoren und Tensoren von einem Koordinatensystem in ein anderes transformiert werden. Solche Ausdrücke werden dann für jedes krummlinige Koordinatensystem gültig.

Ein krummliniges Koordinatensystem kann für einige Anwendungen einfacher zu verwenden sein als das kartesische Koordinatensystem. Die Bewegung von Teilchen unter dem Einfluss von Zentralkräften ist in Kugelkoordinaten meist leichter zu lösen als in kartesischen Koordinaten; dies trifft auf viele physikalische Probleme mit in R ³ definierter Kugelsymmetrie zu . Gleichungen mit Randbedingungen , die Koordinatenoberflächen für ein bestimmtes krummliniges Koordinatensystem folgen, sind in diesem System möglicherweise einfacher zu lösen. Während man die Bewegung eines Partikels in einer rechteckigen Box mit kartesischen Koordinaten beschreiben könnte, ist die Bewegung in einer Kugel mit Kugelkoordinaten einfacher. Kugelkoordinaten sind die gebräuchlichsten krummlinigen Koordinatensysteme und werden in Geowissenschaften , Kartographie , Quantenmechanik , Relativitätstheorie und Ingenieurwesen verwendet .

Orthogonale krummlinige Koordinaten in 3 Dimensionen

Koordinaten, Basis und Vektoren

Abb. 1 - Koordinatenflächen, Koordinatenlinien und Koordinatenachsen von allgemeinen krummlinigen Koordinaten.

Abb. 2 - Koordinatenflächen, Koordinatenlinien und Koordinatenachsen von Kugelkoordinaten. Oberflächen: r - Kugeln, θ - Kegel, φ - Halbebenen; Linien: r - gerade Balken, θ - vertikale Halbkreise, φ - horizontale Kreise; Achsen: r - gerade Balken, θ - Tangenten an vertikale Halbkreise, φ - Tangenten an horizontale Kreise

Betrachten Sie zunächst den 3D-Raum . Ein Punkt P im 3D-Raum (oder sein Positionsvektor r ) kann mit kartesischen Koordinaten ( x , y , z ) [äquivalent geschrieben ( x ¹ , x ² , x ³ )] definiert werden, durch , wobei e _x , e _y , e _z sind die Standardbasis - Vektoren . ${\displaystyle \mathbf {r} = x\mathbf {e} _{x}+y\mathbf {e} _{y}+z\mathbf {e} _{z}}$

Es kann auch durch seine krummlinigen Koordinaten ( q ¹ , q ² , q ³ ) definiert werden, wenn dieses Zahlentriplett einen einzelnen Punkt eindeutig definiert. Der Zusammenhang zwischen den Koordinaten ist dann durch die invertierbaren Transformationsfunktionen gegeben:

${\displaystyle x=f^{1}(q^{1},q^{2},q^{3}),\,y=f^{2}(q^{1},q^{2 },q^{3}),\,z=f^{3}(q^{1},q^{2},q^{3})}$

${\displaystyle q^{1}=g^{1}(x,y,z),\,q^{2}=g^{2}(x,y,z),\,q^{3} =g^{3}(x,y,z)}$

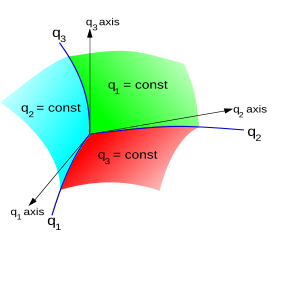
Die Flächen q ¹ = konstant, q ² = konstant, q ³ = konstant werden Koordinatenflächen genannt ; und die durch ihren paarweisen Schnitt gebildeten Raumkurven werden Koordinatenkurven genannt . Die Koordinatenachsen werden durch die Tangenten an die Koordinatenkurven am Schnittpunkt dreier Flächen bestimmt. Sie sind im Allgemeinen keine festen Richtungen im Raum, was bei einfachen kartesischen Koordinaten der Fall ist, und daher gibt es im Allgemeinen keine natürliche globale Basis für krummlinige Koordinaten.

Im kartesischen System können die Standardbasisvektoren aus der Ableitung des Ortes des Punktes P nach der lokalen Koordinate abgeleitet werden

${\displaystyle \mathbf {e} _{x}={\dfrac {\partial \mathbf {r} }{\partial x}};\;\mathbf {e} _{y}={\dfrac {\partial \mathbf {r} }{\partial y}};\;\mathbf {e} _{z}={\dfrac {\partial \mathbf {r} }{\partial z}}.}$

Die Anwendung der gleichen Ableitungen auf das krummlinige System lokal im Punkt P definiert die natürlichen Basisvektoren:

${\displaystyle \mathbf {h} _{1}={\dfrac {\partial \mathbf {r} }{\partial q^{1}}};\;\mathbf {h} _{2}={\ dfrac {\partial\mathbf{r}}{\partialq^{2}}};\;\mathbf{h}_{3}={\dfrac{\partial\mathbf{r}}{\partialq^ {3}}}.}$

Eine solche Basis, deren Vektoren ihre Richtung und/oder ihren Betrag von Punkt zu Punkt ändern, wird als lokale Basis bezeichnet . Alle mit krummlinigen Koordinaten verknüpften Basen sind notwendigerweise lokal. Basisvektoren, die an allen Punkten gleich sind , sind globale Basen und können nur linearen oder affinen Koordinatensystemen zugeordnet werden .

Für diesen Artikel ist e für die Standardbasis (kartesisch) und h oder b für die krummlinige Basis reserviert .

Diese haben möglicherweise keine Einheitslänge und können auch nicht orthogonal sein. Für den Fall, dass sie an allen Punkten, an denen die Ableitungen wohldefiniert sind, orthogonal sind, definieren wir die Lamé-Koeffizienten(nach Gabriel Lamé ) von

${\displaystyle h_{1}=|\mathbf {h} _{1}|;\;h_{2}=|\mathbf {h} _{2}|;\;h_{3}=|\mathbf { h} _{3}|}$

und die krummlinigen orthonormalen Basisvektoren um

${\displaystyle \mathbf {b} _{1}={\dfrac {\mathbf {h} _{1}}{h_{1}}};\;\mathbf {b} _{2}={\dfrac {\mathbf {h} _{2}}{h_{2}}};\;\mathbf {b} _{3}={\dfrac {\mathbf {h} _{3}}{h_{3} }}.}$

Diese Basisvektoren können durchaus von der Position von P abhängen ; es ist daher notwendig, dass sie nicht über einen Bereich konstant angenommen werden. (Sie bilden technisch eine Basis für das Tangentenbündel von an P und sind somit lokal für P. ) ${\displaystyle \mathbb{R} ^{3}}$

Im Allgemeinen erlauben krummlinige Koordinaten, dass die natürlichen Basisvektoren h _i nicht alle zueinander senkrecht stehen und nicht eine Einheitslänge haben müssen: sie können von beliebiger Größe und Richtung sein. Die Verwendung einer orthogonalen Basis macht Vektormanipulationen einfacher als bei nicht orthogonalen. Einige Gebiete der Physik und des Ingenieurwesens , insbesondere die Strömungsmechanik und die Kontinuumsmechanik , erfordern jedoch nicht orthogonale Grundlagen, um Verformungen und Flüssigkeitstransport zu beschreiben, um komplizierte Richtungsabhängigkeiten physikalischer Größen zu berücksichtigen. Eine Diskussion des allgemeinen Falls erscheint später auf dieser Seite.

Vektorrechnung

Differentialelemente

In orthogonalen krummlinigen Koordinaten, da die gesamte differentielle Änderung in r ist

${\displaystyle d\mathbf {r} ={\dfrac {\partial\mathbf {r} }{\partial q^{1}}}dq^{1}+{\dfrac {\partial\mathbf {r}} {\partialq^{2}}}dq^{2}+{\dfrac {\partial\mathbf{r}}{\partialq^{3}}}dq^{3}=h_{1}dq^ {1}\mathbf {b} _{1}+h_{2}dq^{2}\mathbf {b} _{2}+h_{3}dq^{3}\mathbf {b} _{3} }$

Skalenfaktoren sind also ${\displaystyle h_{i}=\left|{\frac {\partial\mathbf{r}}{\partialq^{i}}}\right|}$

In nicht orthogonalen Koordinaten ist die Länge von die positive Quadratwurzel von (mit Einstein-Summationskonvention ). Die sechs unabhängigen Skalarprodukte g _ij = h _i . h _j der natürlichen Basisvektoren verallgemeinern die drei oben definierten Skalierungsfaktoren für orthogonale Koordinaten. Die neun g _ij sind die Komponenten des metrischen Tensors , der nur drei von Null verschiedene Komponenten in orthogonalen Koordinaten hat: g ₁₁ = h ₁ h ₁ , g ₂₂ = h ₂ h ₂ , g ₃₃ = h ₃ h ₃ . ${\displaystyle d\mathbf {r} =dq^{1}\mathbf {h} _{1}+dq^{2}\mathbf {h} _{2}+dq^{3}\mathbf {h} _{3}}$${\displaystyle d\mathbf {r} \cdot d\mathbf {r} =dq^{i}dq^{j}\mathbf {h} _{i}\cdot \mathbf {h} _{j}}$

Kovariante und kontravariante Basen

Ein Vektor v ( rot ) dargestellt durch • eine Vektorbasis ( gelb , links: e ₁ , e ₂ , e ₃ ), Tangentenvektoren an Koordinatenkurven ( schwarz ) und • eine Kovektorbasis oder Kobasis ( blau , rechts: e ¹ , e ² , e ³ ), Normalenvektoren zu Koordinatenoberflächen ( grau ) im Allgemeinen (nicht notwendigerweise orthogonal ) krummlinige Koordinaten ( q ¹ , q ² , q ³ ). Basis und Kobasis stimmen nicht überein, es sei denn, das Koordinatensystem ist orthogonal.

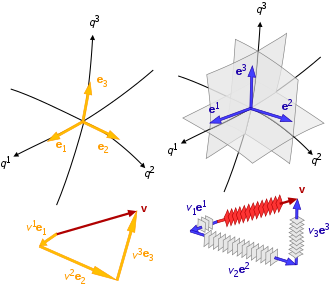
Räumliche Gradienten, Abstände, Zeitableitungen und Skalenfaktoren sind innerhalb eines Koordinatensystems durch zwei Gruppen von Basisvektoren miteinander verbunden:

Folglich hat ein allgemeines krummliniges Koordinatensystem zwei Sätze von Basisvektoren für jeden Punkt: { b ₁ , b ₂ , b ₃ } ist die kovariante Basis und { b ¹ , b ² , b ³ } ist die kontravariante (auch reziproke) Basis. Die kovarianten und kontravarianten Basisvektortypen haben identische Richtungen für orthogonale krummlinige Koordinatensysteme, haben aber wie üblich invertierte Einheiten zueinander.

Beachten Sie die folgende wichtige Gleichheit:

${\displaystyle \mathbf {b} ^{i}\cdot \mathbf {b} _{j}=\delta_{j}^{i}}$

wobei das verallgemeinerte Kronecker-Delta bezeichnet . ${\displaystyle \delta_{j}^{i}}$

Beweis

Im kartesischen Koordinatensystem können wir das Punktprodukt schreiben als: ${\displaystyle (\mathbf{e}_{x},\mathbf{e}_{y},\mathbf{e}_{z})}$ ${\displaystyle \mathbf {b} _{i}\cdot \mathbf {b} ^{j}=({\dfrac {\partial x}{\partial q_{i}}},{\dfrac {\partial y }{\partial q_{i}}},{\dfrac {\partial z}{\partial q_{i}}})\cdot ({\dfrac {\partial q_{j}}{\partial x}}, {\dfrac {\partial q_{j}}{\partial y}},{\dfrac {\partial q_{j}}{\partial z}})={\dfrac {\partial x}{\partial q_{ i}}}{\dfrac {\partial q_{j}}{\partial x}}+{\dfrac {\partial y}{\partial q_{i}}}{\dfrac {\partial q_{j}} {\partial y}}+{\dfrac {\partial z}{\partial q_{i}}}{\dfrac {\partial q_{j}}{\partial z}}}$ Betrachten Sie eine infinitesimale Verschiebung . dq 1 , dq 2 und dq 3 bezeichnen die entsprechenden infinitesimalen Änderungen der krummlinigen Koordinaten q 1 , q 2 bzw. q 3 . ${\displaystyle d\mathbf {r} =dx\cdot \mathbf {e} _{x}+dy\cdot \mathbf {e} _{y}+dz\cdot \mathbf {e} _{z}}$ Nach der Kettenregel lässt sich dq 1 wie folgt ausdrücken: ${\displaystyle dq_{1}={\dfrac {\partial q_{1}}{\partial x}}dx+{\dfrac {\partial q_{1}}{\partial y}}dy+{\dfrac {\partial q_{1}}{\partial z}}dz={\dfrac {\partial q_{1}}{\partial x}}dx+{\dfrac {\partial q_{1}}{\partial y}}({ \dfrac {\partial y}{\partial q_{1}}}dq_{1}+{\dfrac {\partial y}{\partial q_{2}}}dq_{2}+{\dfrac {\partial y }{\partial q_{3}}dq_{3})+{\dfrac {\partial q_{1}}{\partial z}}({\dfrac {\partial z}{\partial q_{1}} }dq_{1}+{\dfrac {\partial z}{\partial q_{2}}}dq_{2}+{\dfrac {\partial z}{\partial q_{3}}}dq_{3}) }$ Ist die Verschiebung d r so, dass dq 2 = dq 3 = 0 ist, dh der Positionsvektor r bewegt sich um einen infinitesimalen Betrag entlang der Koordinatenachse q 2 =const und q 3 =const, dann gilt: ${\displaystyle dq_{1}={\dfrac {\partial q_{1}}{\partial x}}dx+{\dfrac {\partial q_{1}}{\partial y}}{\dfrac {\partial y }{\partial q_{1}}}dq_{1}+{\dfrac {\partial q_{1}}{\partial z}}{\dfrac {\partial z}{\partial q_{1}}}dq_ {1}}$ Dividieren durch dq 1 , und nehmen den Grenzwert dq 1 → 0: ${\displaystyle 1={\dfrac {\partial q_{1}}{\partial x}}{\dfrac {\partial x}{\partial q_{1}}}+{\dfrac {\partial q_{1} }{\partial y}}{\dfrac {\partial y}{\partial q_{1}}}+{\dfrac {\partial q_{1}}{\partial z}}{\dfrac {\partial z} {\partial q_{1}}}={\dfrac {\partial x}{\partial q_{1}}}{\dfrac {\partial q_{1}}{\partial x}}+{\dfrac {\ partiell y}{\partial q_{1}}}{\dfrac {\partial q_{1}}{\partial y}}+{\dfrac {\partial z}{\partial q_{1}}}{\dfrac {\partialq_{1}}{\partialz}}}$ oder gleichwertig: ${\displaystyle \mathbf {b} _{1}\cdot \mathbf {b} ^{1}=1}$ Ist nun die Verschiebung d r so, dass dq 1 = dq 3 = 0 ist, dh der Ortsvektor r bewegt sich um einen infinitesimalen Betrag entlang der Koordinatenachse q 1 =const und q 3 =const, dann gilt: ${\displaystyle 0={\dfrac {\partial q_{1}}{\partial x}}dx+{\dfrac {\partial q_{1}}{\partial y}}{\dfrac {\partial y}{\ partiell q_{2}}}dq_{2}+{\dfrac {\partial q_{1}}{\partial z}}{\dfrac {\partial z}{\partial q_{2}}}dq_{2} }$ Dividieren durch dq 2 , und nehmen den Grenzwert dq 2 → 0: ${\displaystyle 0={\dfrac {\partial q_{1}}{\partial x}}{\dfrac {\partial x}{\partial q_{2}}}}+{\dfrac {\partial q_{1} }{\partial y}}{\dfrac {\partial y}{\partial q_{2}}}+{\dfrac {\partial q_{1}}{\partial z}}{\dfrac {\partial z} {\partial q_{2}}}={\dfrac {\partial x}{\partial q_{2}}}{\dfrac {\partial q_{1}}{\partial x}}+{\dfrac {\ partielles y}{\partiales q_{2}}}{\dfrac {\partiales q_{1}}{\partiales y}}+{\dfrac {\partielles z}{\partielles q_{2}}}{\dfrac {\partialq_{1}}{\partialz}}}$ oder gleichwertig: ${\displaystyle \mathbf {b} _{2}\cdot \mathbf {b} ^{1}=0}$ Und so weiter für die anderen Punktprodukte. Alternativer Nachweis: ${\displaystyle \delta_{j}^{i}dq^{j}=dq^{i}=\nabla q^{i}\cdot d\mathbf {r} =\mathbf {b} ^{i} \cdot {\dfrac {\partial\mathbf{r}}}{\partialq^{j}}}dq^{j}=\mathbf{b}^{i}\cdot\mathbf{b}_{j} dq^{j}}$ und die Einstein-Summationskonvention ist impliziert.

Ein Vektor v kann mit beiden Basiswerten angegeben werden, dh

${\displaystyle \mathbf {v} =v^{1}\mathbf {b} _{1}+v^{2}\mathbf {b} _{2}+v^{3}\mathbf {b} _ {3}=v_{1}\mathbf {b} ^{1}+v_{2}\mathbf {b} ^{2}+v_{3}\mathbf {b} ^{3}}$

Unter Verwendung der Einsteinschen Summationskonvention beziehen sich die Basisvektoren auf die Komponenten um

${\displaystyle \mathbf {v} \cdot \mathbf {b} ^{i}=v^{k}\mathbf {b} _{k}\cdot \mathbf {b} ^{i}=v^{k }\delta_{k}^{i}=v^{i}}$

${\displaystyle \mathbf {v} \cdot \mathbf {b} _{i}=v_{k}\mathbf {b} ^{k}\cdot \mathbf {b} _{i}=v_{k}\ Delta_{i}^{k}=v_{i}}$

und

${\displaystyle \mathbf {v} \cdot \mathbf {b} _{i}=v^{k}\mathbf {b} _{k}\cdot \mathbf {b} _{i}=g_{ki} v^{k}}$

${\displaystyle \mathbf {v} \cdot \mathbf {b} ^{i}=v_{k}\mathbf {b} ^{k}\cdot \mathbf {b} ^{i}=g^{ki} v_{k}}$

wobei g der metrische Tensor ist (siehe unten).

Ein Vektor kann mit kovarianten Koordinaten (erniedrigte Indizes, geschrieben v _k ) oder kontravarianten Koordinaten (erhöhte Indizes, geschrieben v ^k ) angegeben werden. Aus den obigen Vektorsummen ist ersichtlich, dass kontravariante Koordinaten kovarianten Basisvektoren zugeordnet sind und kovariante Koordinaten kontravarianten Basisvektoren zugeordnet sind.

Ein wesentliches Merkmal der Darstellung von Vektoren und Tensoren in Form von indizierten Komponenten und Basisvektoren ist die Invarianz in dem Sinne, dass Vektorkomponenten, die sich kovariant (oder kontravariant) transformieren, mit Basisvektoren gepaart werden, die sich kontravariant transformieren (oder kovariante Weise).

Integration

Konstruieren einer kovarianten Basis in einer Dimension

Abb. 3 – Transformation der lokalen kovarianten Basis bei allgemeinen krummlinigen Koordinaten

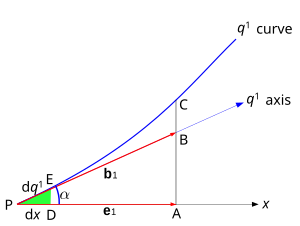
Betrachten Sie die in Fig. 3 gezeigte eindimensionale Kurve. Am Punkt P , der als Ursprung genommen wird , ist x eine der kartesischen Koordinaten und q ¹ ist eine der krummlinigen Koordinaten. Der lokale (nicht-einheitliche) Basisvektor ist b ₁ ( oben mit h _{1 bezeichnet} , wobei b für Einheitsvektoren reserviert ist) und er ist auf der q ¹ -Achse aufgebaut, die eine Tangente zu dieser Koordinatenlinie am Punkt P ist . Die Achse q ¹ und damit der Vektor b ₁ bilden mit der kartesischen x- Achse und dem kartesischen Basisvektor e ₁ einen Winkel . ${\displaystyle\alpha}$

Aus dem Dreieck PAB ist ersichtlich, dass

${\displaystyle \cos\alpha ={\cfrac {|\mathbf {e} _{1}|}{|\mathbf {b} _{1}|}}\quad \Rightarrow \quad |\mathbf {e} _{1}|=|\mathbf{b} _{1}|\cos\alpha}$

wo | e ₁ |, | b ₁ | sind die Beträge der beiden Basisvektoren, dh der skalaren Achsenabschnitte PB und PA . PA ist auch die Projektion von b ₁ auf die x- Achse.

Dieses Verfahren für Basisvektortransformationen mit Richtungskosinus ist jedoch aus folgenden Gründen auf krummlinige Koordinaten nicht anwendbar:

1. Durch Vergrößerung des Abstands von P weicht der Winkel zwischen der gekrümmten Linie q ¹ und der kartesischen Achse x zunehmend von ab .${\displaystyle\alpha}$
2. Im Abstand PB ist der wahre Winkel derjenige, den die Tangente am Punkt C mit der x- Achse bildet und der letztere Winkel ist deutlich verschieden von .${\displaystyle\alpha}$

Die Winkel, die die q ¹ -Linie und diese Achse mit der x- Achse bilden, nähern sich dem Wert an, je näher man sich dem Punkt P nähert und werden bei P genau gleich .

Sei der Punkt E sehr nahe bei P , so nahe, dass der Abstand PE infinitesimal klein ist. Dann PE auf der gemessenen q ¹ Achse nahezu zusammenfällt mit PE auf der gemessenen q ¹ Zeile. Gleichzeitig wird das Verhältnis PD/PE ( PD ist die Projektion von PE auf die x- Achse) fast genau gleich . ${\displaystyle \cos\alpha}$

Die infinitesimal kleinen Achsenabschnitte PD und PE seien mit dx bzw. d q ^{1 bezeichnet} . Dann

${\displaystyle \cos\alpha ={\cfrac {dx}{dq^{1}}}={\frac {|\mathbf {e} _{1}|}{|\mathbf {b} _{1} |}}}$.

Somit können die Richtungskosinus in Transformationen mit den genaueren Verhältnissen zwischen infinitesimal kleinen Koordinatenabschnitten ersetzt werden. Daraus folgt, dass die Komponente (Projektion) von b ₁ auf der x- Achse ist

${\displaystyle p^{1}=\mathbf {b} _{1}\cdot {\cfrac {\mathbf {e} _{1}}{|\mathbf {e} _{1}|}}=| \mathbf {b} _{1}|{\cfrac {|\mathbf {e} _{1}|}{|\mathbf {e} _{1}|}}\cos \alpha =|\mathbf {b } _{1}|{\cfrac {dx}{dq^{1}}}\quad \Rightarrow \quad {\cfrac {p^{1}}{|\mathbf {b} _{1}|}} ={\cfrac {dx}{dq^{1}}}}$.

Wenn q ⁱ = q ⁱ ( x ₁ , x ₂ , x ₃ ) und x _i = x _i ( q ¹ , q ² , q ³ ) glatte (stetig differenzierbare) Funktionen sind, können die Transformationsverhältnisse als und geschrieben werden . Das heißt, diese Verhältnisse sind partielle Ableitungen von Koordinaten, die zu einem System gehören, in Bezug auf Koordinaten, die zu dem anderen System gehören. ${\displaystyle {\cfrac {\partial q^{i}}{\partial x_{j}}}}$${\displaystyle {\cfrac {\partial x_{i}}{\partial q^{j}}}}$

Konstruieren einer kovarianten Basis in drei Dimensionen

Wenn Sie dasselbe für die Koordinaten in den anderen 2 Dimensionen tun, kann b ₁ ausgedrückt werden als:

${\displaystyle \mathbf {b} _{1}=p^{1}\mathbf {e} _{1}+p^{2}\mathbf {e} _{2}+p^{3}\mathbf {e} _{3}={\cfrac {\partial x_{1}}{\partial q^{1}}}\mathbf {e} _{1}+{\cfrac {\partial x_{2}} {\partial q^{1}}}\mathbf {e} _{2}+{\cfrac {\partial x_{3}}{\partial q^{1}}}\mathbf {e} _{3} }$

Ähnliche Gleichungen gelten für b ₂ und b ₃ , so dass die Standardbasis { e ₁ , e ₂ , e ₃ } ist mit einer lokalen transformiert (geordnete und normalisierte ) Basis { b ₁ , b ₂ , b ₃ } durch das folgende System von Gleichungen:

${\displaystyle {\begin{ausgerichtet}\mathbf {b} _{1}&={\cfrac {\partial x_{1}}{\partial q^{1}}}\mathbf {e} _{1} +{\cfrac {\partial x_{2}}{\partial q^{1}}}\mathbf {e} _{2}+{\cfrac {\partial x_{3}}{\partial q^{1 }}}\mathbf {e} _{3}\\\mathbf {b} _{2}&={\cfrac {\partial x_{1}}{\partial q^{2}}}\mathbf {e } _{1}+{\cfrac {\partial x_{2}}{\partial q^{2}}}\mathbf {e} _{2}+{\cfrac {\partial x_{3}}{\ partielles q^{2}}}\mathbf {e} _{3}\\\mathbf {b} _{3}&={\cfrac {\partial x_{1}}{\partielles q^{3}} }\mathbf {e} _{1}+{\cfrac {\partial x_{2}}{\partial q^{3}}}\mathbf {e} _{2}+{\cfrac {\partial x_{ 3}}{\partial q^{3}}}\mathbf{e} _{3}\end{ausgerichtet}}}$

Durch analoge Argumentation kann man die inverse Transformation von der lokalen Basis in die Standardbasis erhalten:

${\displaystyle {\begin{ausgerichtet}\mathbf {e} _{1}&={\cfrac {\partial q^{1}}{\partial x_{1}}}\mathbf {b} _{1} +{\cfrac {\partial q^{2}}{\partial x_{1}}}\mathbf {b} _{2}+{\cfrac {\partial q^{3}}{\partial x_{1 }}}\mathbf {b} _{3}\\\mathbf {e} _{2}&={\cfrac {\partial q^{1}}{\partial x_{2}}}\mathbf {b } _{1}+{\cfrac {\partial q^{2}}{\partial x_{2}}}\mathbf {b} _{2}+{\cfrac {\partial q^{3}}{ \partial x_{2}}}\mathbf {b} _{3}\\\mathbf {e} _{3}&={\cfrac {\partial q^{1}}{\partial x_{3}} }\mathbf {b} _{1}+{\cfrac {\partial q^{2}}{\partial x_{3}}}\mathbf {b} _{2}+{\cfrac {\partial q^ {3}}{\partial x_{3}}}\mathbf {b} _{3}\end{ausgerichtet}}}$

Jacobi der Transformation

Die obigen linearen Gleichungssysteme können in Matrixform unter Verwendung der Einsteinschen Summationskonvention geschrieben werden als

${\displaystyle {\cfrac {\partial x_{i}}{\partial q^{k}}}\mathbf {e} _{i}=\mathbf {b} _{k},\quad {\cfrac { \partialq^{i}}{\partialx_{k}}}\mathbf{b}_{i}=\mathbf{e}_{k}}$.

Diese Koeffizientenmatrix des linearen Systems ist die Jacobi-Matrix (und ihre Umkehrung) der Transformation. Dies sind die Gleichungen, die verwendet werden können, um eine kartesische Basis in eine krummlinige Basis umzuwandeln und umgekehrt.

In drei Dimensionen sind die erweiterten Formen dieser Matrizen

${\displaystyle \mathbf{J} ={\begin{bmatrix}{\cfrac {\partial x_{1}}{\partial q^{1}}}&{\cfrac {\partial x_{1}}{\ partielles q^{2}}}&{\cfrac {\partiales x_{1}}{\partiales q^{3}}}\\{\cfrac {\partielles x_{2}}{\partielles q^{1 }}}&{\cfrac {\partial x_{2}}{\partial q^{2}}}}&{\cfrac {\partial x_{2}}{\partial q^{3}}}\\{ \cfrac {\partial x_{3}}{\partial q^{1}}}&{\cfrac {\partial x_{3}}{\partial q^{2}}}&{\cfrac {\partial x_ {3}}{\partial q^{3}}\\\end{bmatrix}},\quad\mathbf{J}^{-1}={\begin{bmatrix}{\cfrac {\partial q^ {1}}{\partial x_{1}}}&{\cfrac {\partial q^{1}}{\partial x_{2}}}}&{\cfrac {\partial q^{1}}{\ partielles x_{3}}}\\{\cfrac {\partiales q^{2}}{\partiales x_{1}}}&{\cfrac {\partiales q^{2}}{\partielles x_{2} }}&{\cfrac {\partial q^{2}}{\partial x_{3}}}\\{\cfrac {\partial q^{3}}{\partial x_{1}}}&{\ cfrac {\partial q^{3}}{\partial x_{2}}}&{\cfrac {\partial q^{3}}{\partial x_{3}}}\\\end{bmatrix}}}$

Bei der Rücktransformation (zweites Gleichungssystem) sind die Unbekannten die krummlinigen Basisvektoren. Für einen bestimmten Ort kann es nur einen und nur einen Satz von Basisvektoren geben (sonst ist die Basis an diesem Punkt nicht gut definiert). Diese Bedingung ist genau dann erfüllt, wenn das Gleichungssystem eine einzige Lösung hat. In der linearen Algebra hat ein lineares Gleichungssystem nur dann eine einzige Lösung (nicht trivial), wenn die Determinante seiner Systemmatrix ungleich Null ist:

${\displaystyle \det(\mathbf{J}^{-1})\neq 0}$

was den Grund für die obige Forderung bezüglich der inversen Jacobi-Determinante zeigt.

Verallgemeinerung auf n Dimensionen

Der Formalismus erstreckt sich wie folgt auf jede endliche Dimension.

Betrachten Sie den reellen euklidischen n- dimensionalen Raum, d. h. R ⁿ = R × R × ... × R ( n mal), wobei R die Menge der reellen Zahlen und × das kartesische Produkt bezeichnet , das ein Vektorraum ist .

Die Koordinaten dieses Raumes können bezeichnet werden durch: x = ( x ₁ , x ₂ ,..., x _n ). Da dies ein Vektor (ein Element des Vektorraums) ist, kann er geschrieben werden als:

${\displaystyle \mathbf{x} =\sum_{i=1}^{n}x_{i}\mathbf{e}^{i}}$

wobei e ¹ = (1,0,0...,0), e ² = (0,1,0...,0), e ³ = (0,0,1...,0),. .., e ⁿ = (0,0,0...,1) ist der Standardbasissatz von Vektoren für den Raum R ⁿ , und i = 1, 2,... n ist ein Index, der Komponenten kennzeichnet. Jeder Vektor hat genau eine Komponente in jeder Dimension (oder "Achse") und sie sind zueinander orthogonal ( senkrecht ) und normalisiert (hat Einheitsgröße ).

Allgemeiner können wir Basisvektoren b _i so definieren, dass sie von q = ( q ₁ , q ₂ ,..., q _n ) abhängen , dh sie ändern sich von Punkt zu Punkt: b _i = b _i ( q ). In diesem Fall wird die gleichen Punkt zu definieren x die: im Sinne dieser alternativen Basiskoordinaten in Bezug auf diese Basis v _i auf notwendigerweise auch abhängen x auch, das heißt v _i = v _i ( x ). Dann kann ein Vektor v in diesem Raum bezüglich dieser alternativen Koordinaten und Basisvektoren als Linearkombination in dieser Basis entwickelt werden (was einfach bedeutet, jeden Basisvektor e _i mit einer Zahl v _{i zu} multiplizieren – Skalarmultiplikation ):

${\displaystyle \mathbf {v} =\sum _{j=1}^{n}{\bar {v}}^{j}\mathbf {b} _{j}=\sum _{j=1} ^{n}{\bar{v}}^{j}(\mathbf{q})\mathbf{b}_{j}(\mathbf{q})}$

Die Vektorsumme, die v in der neuen Basis beschreibt, setzt sich aus verschiedenen Vektoren zusammen, wobei die Summe selbst gleich bleibt.

Transformation von Koordinaten

Aus einer allgemeineren und abstrakteren Perspektive ist ein krummliniges Koordinatensystem einfach ein Koordinatenfeld auf der differenzierbaren Mannigfaltigkeit E ⁿ (n-dimensionaler euklidischer Raum ), das diffeomorph zum kartesischen Koordinatenfeld auf der Mannigfaltigkeit ist. Zwei diffeomorphe Koordinatenfelder auf einer Differentialmannigfaltigkeit müssen sich nicht differenziell überlappen. Mit dieser einfachen Definition eines krummlinigen Koordinatensystems sind alle folgenden Ergebnisse einfach Anwendungen von Standardsätzen in der Differentialtopologie .

Die Transformationsfunktionen sind so, dass zwischen Punkten in den "alten" und "neuen" Koordinaten eine Eins-zu-Eins-Beziehung besteht, d. h. diese Funktionen sind Bijektionen und erfüllen die folgenden Anforderungen innerhalb ihrer Domänen :

Vektor- und Tensoralgebra in dreidimensionalen krummlinigen Koordinaten

Hinweis: Im Folgenden wird die Einstein-Summierungskonvention des Summierens bei wiederholten Indizes verwendet.

Die elementare Vektor- und Tensoralgebra in krummlinigen Koordinaten wird in einigen der älteren wissenschaftlichen Literatur der Mechanik und Physik verwendet und kann für das Verständnis von Arbeiten aus dem frühen und mittleren Jahrtausend, zum Beispiel dem Text von Green und Zerna, unverzichtbar sein. In diesem Abschnitt werden einige nützliche Beziehungen in der Algebra von Vektoren und Tensoren zweiter Ordnung in krummlinigen Koordinaten angegeben. Notation und Inhalt stammen hauptsächlich von Ogden, Naghdi, Simmonds, Green und Zerna, Basar und Weichert und Ciarlet.

Tensoren in krummlinigen Koordinaten

Ein Tensor zweiter Ordnung kann ausgedrückt werden als

${\displaystyle {\boldsymbol {S}}=S^{ij}\mathbf {b} _{i}\otimes \mathbf {b} _{j}=S^{i}{}_{j}\mathbf {b} _{i}\otimes \mathbf {b} ^{j}=S_{i}{}^{j}\mathbf {b} ^{i}\otimes \mathbf {b} _{j}= S_{ij}\mathbf{b}^{i}\otimes\mathbf{b}^{j}}$

wobei bezeichnet das Tensorprodukt . Die Komponenten S ^ij werden als kontravariante Komponenten bezeichnet, S ⁱ _j als gemischte rechtskovariante Komponenten, S _i ^j als gemischte linkskovariante Komponenten und S _ij als kovariante Komponenten des Tensors zweiter Ordnung. Die Komponenten des Tensors zweiter Ordnung stehen in Beziehung zu ${\displaystyle \scriptstyle \otimes}$

${\displaystyle S^{ij}=g^{ik}S_{k}{}^{j}=g^{jk}S^{i}{}_{k}=g^{ik}g^{ j\ell}S_{k\ell}}$

Der metrische Tensor in orthogonalen krummlinigen Koordinaten

An jedem Punkt kann man ein kleines Linienelement d x konstruieren , so dass das Quadrat der Länge des Linienelements das Skalarprodukt d x • d x ist und als Metrik des Raums bezeichnet wird , gegeben durch:

${\displaystyle d\mathbf {x} \cdot d\mathbf {x} ={\cfrac {\partial x_{i}}{\partial q^{j}}}{\cfrac {\partial x_{i}} {\partial q^{k}}}dq^{j}dq^{k}}$.

Der folgende Teil der obigen Gleichung

${\displaystyle {\cfrac {\partial x_{k}}{\partial q^{i}}}{\cfrac {\partial x_{k}}{\partial q^{j}}}=g_{ij} (q^{i},q^{j})=\mathbf{b}_{i}\cdot\mathbf{b}_{j}}$

ist ein symmetrischer Tensor, der als fundamentaler (oder metrischer) Tensor des euklidischen Raums in krummlinigen Koordinaten bezeichnet wird.

Indizes können durch die Metrik erhöht und gesenkt werden:

${\displaystyle v^{i}=g^{ik}v_{k}}$

Beziehung zu Lamé-Koeffizienten

Definition der Skalierungsfaktoren h _i durch _i

${\displaystyle h_{i}h_{j}=g_{ij}=\mathbf {b} _{i}\cdot \mathbf {b} _{j}\quad \Rightarrow \quad h_{i}={\ sqrt {g_{ii}}}=\left|\mathbf {b}_{i}\right|=\left|{\cfrac {\partial\mathbf{x} }{\partial q^{i}}} \rechts|}$

gibt eine Beziehung zwischen dem metrischen Tensor und den Lamé-Koeffizienten an, und

${\displaystyle g_{ij}={\cfrac {\partial \mathbf {x} }{\partial q^{i}}}\cdot {\cfrac {\partial\mathbf {x} }{\partial q^{ j}}}=\left(h_{ki}\mathbf{e}_{k}\right)\cdot \left(h_{mj}\mathbf{e}_{m}\right)=h_{ki} h_{kj}}$

wobei h _ij die Lamé-Koeffizienten sind. Für eine orthogonale Basis haben wir auch:

${\displaystyle g=g_{11}g_{22}g_{33}=h_{1}^{2}h_{2}^{2}h_{3}^{2}\quad \Rightarrow \quad {\ Quadrat {g}}=h_{1}h_{2}h_{3}=J}$

Beispiel: Polarkoordinaten

Betrachten wir Polarkoordinaten für R ² ,

${\displaystyle (x,y)=(r\cos\theta,r\sin\theta)}$

(r, θ) sind die krummlinigen Koordinaten, und die Jacobi-Determinante der Transformation ( r ,θ) → ( r cos θ, r sin θ) ist r .

Die orthogonalen Basisvektoren sind b _r = (cos θ, sin θ), b _θ = (−r sin θ, r cos ). Die Skalierungsfaktoren sind h _r = 1 und h _θ = r . Der Fundamentaltensor ist g ₁₁ = 1, g ₂₂ = r ² , g ₁₂ = g ₂₁ = 0.

Der alternierende Tensor

In einer orthonormalen rechtshändigen Basis ist der alternierende Tensor dritter Ordnung definiert als

${\displaystyle {\boldsymbol {\mathcal {E}}}=\varepsilon_{ijk}\mathbf {e} ^{i}\otimes \mathbf {e} ^{j}\otimes \mathbf {e} ^{ k}}$

In einer allgemeinen krummlinigen Basis kann derselbe Tensor ausgedrückt werden als

${\displaystyle {\boldsymbol {\mathcal{E}}}={\mathcal{E}}_{ijk}\mathbf {b} ^{i}\otimes \mathbf {b} ^{j}\otimes \mathbf {b} ^{k}={\mathcal{E}}^{ijk}\mathbf {b} _{i}\otimes \mathbf {b} _{j}\otimes \mathbf {b} _{k} }$

Es kann auch gezeigt werden, dass

${\displaystyle {\mathcal {E}}^{ijk}={\cfrac {1}{J}}\varepsilon _{ijk}={\cfrac {1}{+{\sqrt {g}}}}\ varepsilon_{ijk}}$

Christoffel-Symbole

Christoffel-Symbole erster Art${\displaystyle \Gamma_{kij}}$

${\displaystyle \mathbf {b} _{i,j}={\frac {\partial \mathbf {b} _{i}}{\partial q^{j}}}=\mathbf {b} ^{k }\Gamma_{kij}\quad\Rightarrow\quad\mathbf{b}_{k}\cdot\mathbf{b}_{i,j}=\Gamma_{kij}}$

wobei das Komma eine partielle Ableitung bezeichnet (siehe Ricci-Kalkül ). Um Γ _kij durch g _ij auszudrücken ,

${\displaystyle {\begin{ausgerichtet}g_{ij,k}&=(\mathbf {b} _{i}\cdot \mathbf {b} _{j})_{,k}=\mathbf {b} _{i,k}\cdot \mathbf {b} _{j}+\mathbf {b} _{i}\cdot \mathbf {b} _{j,k}=\Gamma_{jik}+\Gamma _{ijk}\\g_{ik,j}&=(\mathbf {b} _{i}\cdot \mathbf {b} _{k})_{,j}=\mathbf {b} _{i ,j}\cdot\mathbf{b}_{k}+\mathbf{b}_{i}\cdot\mathbf{b}_{k,j}=\Gamma_{kij}+\Gamma_{ikj }\\g_{jk,i}&=(\mathbf{b}_{j}\cdot \mathbf{b}_{k})_{,i}=\mathbf{b}_{j,i} \cdot\mathbf{b}_{k}+\mathbf{b}_{j}\cdot\mathbf{b}_{k,i}=\Gamma_{kji}+\Gamma_{jki}\end {ausgerichtet}}}$

Schon seit

${\displaystyle \mathbf {b} _{i,j}=\mathbf {b} _{j,i}\quad \Rightarrow\quad\Gamma_{kij}=\Gamma_{kji}}$

wenn man diese verwendet, um die obigen Beziehungen neu anzuordnen, erhält man

${\displaystyle \Gamma_{kij}={\frac {1}{2}}(g_{ik,j}+g_{jk,i}-g_{ij,k})={\frac {1}{ 2}}[(\mathbf{b}_{i}\cdot\mathbf{b}_{k})_{,j}+(\mathbf{b}_{j}\cdot\mathbf{b}_ {k})_{,i}-(\mathbf{b}_{i}\cdot \mathbf{b}_{j})_{,k}]}$

Christoffel-Symbole zweiter Art${\displaystyle \Gamma^{k}{}_{ji}}$

${\displaystyle \Gamma^{k}{}_{ij}=g^{kl}\Gamma_{lij}=\Gamma^{k}{}_{ji},\quad {\cfrac {\partial\ mathbf {b} _{i}}{\partial q^{j}}}=\mathbf {b} _{k}\Gamma ^{k}{}_{ij}}$

Dies impliziert, dass

${\displaystyle \Gamma^{k}{}_{ij}={\cfrac {\partial \mathbf {b} _{i}}{\partial q^{j}}}\cdot \mathbf {b} ^ {k}=-\mathbf {b} _{i}\cdot {\cfrac {\partial \mathbf {b} ^{k}}{\partial q^{j}}}\quad}$seit .${\displaystyle \quad {\cfrac {\partial}{\partialq^{j}}}(\mathbf{b}_{i}\cdot\mathbf{b}^{k})=0}$

Andere Beziehungen, die folgen, sind

${\displaystyle {\cfrac {\partial \mathbf {b} ^{i}}{\partial q^{j}}}=-\Gamma ^{i}{}_{jk}\mathbf {b} ^{ k},\quad {\boldsymbol {\nabla}}\mathbf {b} _{i}=\Gamma^{k}{}_{ij}\mathbf {b} _{k}\otimes \mathbf {b } ^{j},\quad {\boldsymbol {\nabla}}\mathbf {b} ^{i}=-\Gamma ^{i}{}_{jk}\mathbf {b} ^{k}\otimes \mathbf{b} ^{j}}$

Vektoroperationen

Vektor- und Tensorrechnung in dreidimensionalen krummlinigen Koordinaten

Hinweis: Im Folgenden wird die Einstein-Summierungskonvention des Summierens bei wiederholten Indizes verwendet.

Anpassungen müssen bei der Berechnung der gemacht werden Linie , Fläche und Volumen Integrale . Der Einfachheit halber beschränkt sich das Folgende auf drei Dimensionen und orthogonale krummlinige Koordinaten. Die gleichen Argumente gelten jedoch für n- dimensionale Räume. Wenn das Koordinatensystem nicht orthogonal ist, enthalten die Ausdrücke einige zusätzliche Begriffe.

Simmonds zitiert in seinem Buch über die Tensoranalyse Albert Einsteins Aussage

Die Magie dieser Theorie wird sich kaum jemandem aufdrängen, der sie wirklich verstanden hat; sie stellt einen echten Triumph der Methode der absoluten Differentialrechnung dar, die von Gauß, Riemann, Ricci und Levi-Civita begründet wurde.

Vektor- und Tensorrechnung in allgemeinen krummlinigen Koordinaten wird in der Tensoranalyse an vierdimensionalen krummlinigen Mannigfaltigkeiten in der Allgemeinen Relativitätstheorie , in der Mechanik gekrümmter Schalen , bei der Untersuchung der Invarianzeigenschaften von Maxwell-Gleichungen verwendet, was in Metamaterialien und in vielen anderen Bereichen von Interesse war .

In diesem Abschnitt werden einige nützliche Beziehungen in der Berechnung von Vektoren und Tensoren zweiter Ordnung in krummlinigen Koordinaten gegeben. Notation und Inhalt stammen hauptsächlich von Ogden, Simmonds, Green und Zerna, Basar und Weichert und Ciarlet.

Seien φ = φ( x ) ein wohldefiniertes Skalarfeld und v = v ( x ) ein wohldefiniertes Vektorfeld, und λ ₁ , λ ₂ ... seien Parameter der Koordinaten

Geometrische Elemente

Integration

Operator	Skalarfeld	Vektorfeld
Linienintegral	${\displaystyle \int_{C}\varphi (\mathbf{x})ds=\int_{a}^{b}\varphi (\mathbf{x} (\lambda))\left|{\partial\ mathbf{x}\over\partial\lambda}\right|d\lambda}$	${\displaystyle \int _{C}\mathbf {v} (\mathbf {x} )\cdot d\mathbf {s} =\int _{a}^{b}\mathbf {v} (\mathbf {x } (\lambda))\cdot \left({\partial\mathbf{x}\over\partial\lambda}\right)d\lambda}$
Flächenintegral	${\displaystyle \int_{S}\varphi (\mathbf{x})dS=\iint_{T}\varphi (\mathbf{x} (\lambda_{1},\lambda_{2})) \left|{\partial\mathbf{x}\over\partial\lambda_{1}}\times {\partial\mathbf{x}\over\partial\lambda_{2}}\right|d\lambda_ {1}d\lambda_{2}}$	${\displaystyle \int _{S}\mathbf {v} (\mathbf {x} )\cdot dS=\iint _{T}\mathbf {v} (\mathbf {x} (\lambda _{1}, \lambda_{2}))\cdot \left({\partial\mathbf{x}\over\partial\lambda_{1}}\times {\partial\mathbf{x}\over\partial\lambda_{ 2}}\right)d\lambda_{1}d\lambda_{2}}$
Volumenintegral	${\displaystyle \iiiint_{V}\varphi (x,y,z)dV=\iiiint_{V}\chi (q_{1},q_{2},q_{3})Jdq_{1}dq_{ 2}dq_{3}}$	${\displaystyle \iiiint_{V}\mathbf {u} (x,y,z)dV=\iiiint_{V}\mathbf {v} (q_{1},q_{2},q_{3}) Jdq_{1}dq_{2}dq_{3}}$

Unterscheidung

Die Ausdrücke für den Gradienten, die Divergenz und den Laplace-Operator können direkt auf n- Dimensionen erweitert werden, jedoch ist die Krümmung nur in 3D definiert.

Das Vektorfeld b _i tangiert die q ⁱ -Koordinatenkurve und bildet an jedem Punkt der Kurve eine natürliche Basis . Diese Basis wird, wie zu Beginn dieses Artikels diskutiert, auch als kovariante krummlinige Basis bezeichnet. Wir können auch eine reziproke Basis oder kontravariante krummlinige Basis b ^{i definieren} . Alle algebraischen Beziehungen zwischen den Basisvektoren, wie sie im Abschnitt über die Tensoralgebra diskutiert wurden, gelten für die natürliche Basis und ihren Kehrwert an jedem Punkt x .

Operator	Skalarfeld	Vektorfeld	Tensorfeld 2. Ordnung
Gradient	${\displaystyle\nabla\varphi={\cfrac{1}{h_{i}}}{\partial\varphi\over\partialq^{i}}\mathbf{b}^{i}}$	${\displaystyle \nabla\mathbf{v} ={\cfrac {1}{h_{i}^{2}}}{\partial\mathbf{v}\over\partialq^{i}}\otimes\mathbf {b} _{i}}$	${\displaystyle {\boldsymbol {\nabla}}{\boldsymbol {S}}={\cfrac {\partial {\boldsymbol {S}}}{\partial q^{i}}}\otimes \mathbf {b} ^{i}}$
Abweichungen	N / A	${\displaystyle \nabla\cdot\mathbf{v} ={\cfrac {1}{\prod_{j}h_{j}}}{\frac {\partial }{\partial q^{i}}}( v^{i}\prod_{j\neq i}h_{j})}$	${\displaystyle ({\boldsymbol {\nabla}}\cdot {\boldsymbol {S}})\cdot \mathbf {a} ={\boldsymbol {\nabla}}\cdot ({\boldsymbol {S}}\cdot \mathbf{a})}$ wobei a ein beliebiger konstanter Vektor ist. In krummlinigen Koordinaten, ${\displaystyle {\boldsymbol {\nabla}}\cdot {\boldsymbol {S}}=\left[{\cfrac {\partial S_{ij}}{\partial q^{k}}}-\Gamma_{ ki}^{l}S_{lj}-\Gamma_{kj}^{l}S_{il}\right]g^{ik}\mathbf {b} ^{j}}$
Laplace	${\displaystyle \nabla^{2}\varphi ={\cfrac {1}{\prod_{j}h_{j}}}{\frac {\partial }{\partial q^{i}}}\left ({\cfrac {\prod_{j}h_{j}}{h_{i}^{2}}}{\frac {\partial \varphi }{\partial q^{i}}}\right)}$
Locken	N / A	Nur für Vektorfelder in 3D, ${\displaystyle \nabla \times \mathbf {v} ={\frac {1}{h_{1}h_{2}h_{3}}}\mathbf {e} _{i}\epsilon _{ijk}h_ {i}{\frac{\partial (h_{k}v_{k})}{\partial q^{j}}}}$ wo ist das Levi-Civita-Symbol . ${\displaystyle \epsilon_{ijk}}$	Siehe Curl eines Tensorfeldes