Verhältnistest - Ratio test

In der Mathematik ist der Quotiententest ein Test (oder "Kriterium") für die Konvergenz einer Reihe

${\displaystyle \sum_{n=1}^{\infty}a_{n},}$

wobei jeder Term eine reelle oder komplexe Zahl ist und a _{n von} Null verschieden ist, wenn n groß ist. Der Test wurde zuerst von Jean le Rond d'Alembert veröffentlicht und wird manchmal als d'Alembert-Ratio-Test oder als Cauchy-Ratio-Test bezeichnet .

Der Test

Entscheidungsdiagramm für den Verhältnistest

Die übliche Form des Tests verwendet den Grenzwert

${\displaystyle L=\lim_{n\to\infty}\left|{\frac {a_{n+1}}{a_{n}}}\right|.}$

( 1 )

Der Verhältnistest besagt, dass:

• wenn L < 1 dann konvergiert die Reihe absolut ;
• wenn L > 1, dann ist die Reihe divergent ;
• falls L = 1 ist oder der Grenzwert nicht existiert, ist der Test nicht schlüssig, da es sowohl konvergente als auch divergente Reihen gibt, die diesen Fall erfüllen.

Es ist möglich, den Verhältnistest auf bestimmte Fälle anzuwenden, in denen der Grenzwert L nicht existiert, wenn Grenzwert höher und Grenzwert niedriger verwendet werden. Die Testkriterien können auch verfeinert werden, sodass der Test manchmal auch bei L = 1 aussagekräftig ist

${\displaystyle R=\lim\sup\left|{\frac {a_{n+1}}{a_{n}}}\right|}$

${\displaystyle r=\lim\inf\left|{\frac {a_{n+1}}{a_{n}}}\right|}$.

Dann besagt der Verhältnistest:

• wenn R < 1, konvergiert die Reihe absolut;
• wenn r > 1 divergiert die Reihe;
• wenn für alle großen n (unabhängig vom Wert von r ) die Reihe auch divergiert; dies liegt daran, dass a _n ungleich Null ist und zunimmt und sich daher a _n nicht Null annähert;${\displaystyle \left|{\frac {a_{n+1}}{a_{n}}}\right|\geq 1}$${\displaystyle |a_{n}|}$
• ansonsten ist der test nicht aussagekräftig.

Falls der Grenzwert L in ( 1 ) existiert, müssen wir L = R = r haben . Der ursprüngliche Verhältnistest ist also eine schwächere Version des verfeinerten.

Beispiele

Konvergent, weil L < 1

Betrachten Sie die Serie

${\displaystyle \sum _{n=1}^{\infty }{\frac {n}{e^{n}}}}$

Mit dem Verhältnistest berechnet man den Grenzwert

${\displaystyle L=\lim_{n\to\infty}\left|{\frac {a_{n+1}}{a_{n}}}\right|=\lim_{n\to\infty} \left|{\frac {\frac {n+1}{e^{n+1}}}{\frac {n}{e^{n}}}}\right|={\frac {1}{ e}}<1.}$

Da dieser Grenzwert kleiner als 1 ist, konvergiert die Reihe.

Divergent, weil L > 1

Betrachten Sie die Serie

${\displaystyle \sum _{n=1}^{\infty }{\frac {e^{n}}{n}}.}$

Setzen Sie dies in den Verhältnistest ein:

${\displaystyle L=\lim_{n\to\infty}\left|{\frac {a_{n+1}}{a_{n}}}\right|=\lim_{n\to\infty} \left|{\frac {\frac {e^{n+1}}{n+1}}{\frac {e^{n}}{n}}}\right|=e>1.}$

Damit divergiert die Reihe.

Nicht schlüssig, da L = 1

Betrachten Sie die drei Serien

${\displaystyle \sum_{n=1}^{\infty}1,}$

${\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{2}}},}$

${\displaystyle \sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}.}$

Die erste Reihe ( 1 + 1 + 1 + 1 + ⋯ ) divergiert, die zweite (die zentrale für das Basler Problem ) konvergiert absolut und die dritte (die alternierende harmonische Reihe ) konvergiert bedingt. Jedoch sind die Größenverhältnisse von Begriff zu Begriff der drei Reihen jeweils    und    . In allen drei Fällen ergibt sich also, dass der Grenzwert gleich 1 ist. Dies zeigt, dass bei L = 1 die Reihe konvergieren oder divergieren kann und daher der ursprüngliche Verhältnistest nicht schlüssig ist. In solchen Fällen sind verfeinerte Tests erforderlich, um Konvergenz oder Divergenz zu bestimmen. ${\displaystyle \left|{\frac {a_{n+1}}{a_{n}}}\right|}$${\displaystyle 1,}$   ${\displaystyle {\frac {n^{2}}{(n+1)^{2}}}}$${\displaystyle {\frac {n}{n+1}}}$${\displaystyle \lim_{n\to\infty}\left|{\frac {a_{n+1}}{a_{n}}}\right|}$

Nachweisen

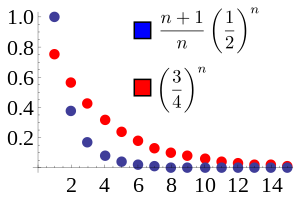
In diesem Beispiel konvergiert das Verhältnis benachbarter Terme in der blauen Folge gegen L=1/2. Wir wählen r  = (L+1)/2 = 3/4. Dann wird die blaue Folge von der roten Folge r ^k für alle n ≥ 2 dominiert . Die rote Folge konvergiert, also auch die blaue Folge.

Unten ist ein Beweis für die Gültigkeit des ursprünglichen Ratio-Tests.

Angenommen, das . Wir können dann zeigen, dass die Reihe absolut konvergiert, indem wir zeigen, dass ihre Terme schließlich kleiner werden als die einer bestimmten konvergenten geometrischen Reihe . Betrachten Sie dazu eine reelle Zahl r mit . Dies impliziert, dass für hinreichend großes n ; sagen wir für alle n größer als N . Also für jedes n > N und i > 0, und so ${\displaystyle L=\lim_{n\to\infty}\left|{\frac {a_{n+1}}{a_{n}}}\right|<1}$ ${\displaystyle L<r<1}$${\displaystyle |a_{n+1}|<r|a_{n}|}$${\displaystyle |a_{n+i}|<r^{i}|a_{n}|}$

${\displaystyle \sum _{i=N+1}^{\infty}|a_{i}|=\sum _{i=1}^{\infty}\left|a_{N+i}\right| <\sum_{i=1}^{\infty}r^{i}|a_{N}|=|a_{N}|\sum_{i=1}^{\infty}r^{i} =|a_{N}|{\frac{r}{1-r}}<\infty.}$

Das heißt, die Reihe konvergiert absolut.

Andererseits, wenn L > 1, dann für ausreichend großes n , so dass die Grenze der Summanden ungleich Null ist. Daher divergiert die Reihe. ${\displaystyle |a_{n+1}|>|a_{n}|}$

Verlängerungen für L = 1

Wie im vorherigen Beispiel zu sehen ist, kann der Verhältnistest nicht schlüssig sein, wenn die Grenze des Verhältnisses 1 ist. Erweiterungen des Verhältnistests ermöglichen es jedoch manchmal, diesen Fall zu behandeln.

Bei allen folgenden Tests wird davon ausgegangen, dass Σ a _n eine Summe mit positivem a _{n ist} . Diese Tests können auch auf jede Reihe mit einer endlichen Anzahl negativer Terme angewendet werden. Jede solche Reihe kann geschrieben werden als:

${\displaystyle \sum _{n=1}^{\infty}a_{n}=\sum _{n=1}^{N}a_{n}+\sum _{n=N+1}^{ \infty}a_{n}}$

wobei a _N der am höchsten indizierte negative Term ist. Der erste Ausdruck rechts ist eine Teilsumme, die endlich ist, und so wird die Konvergenz der gesamten Reihe durch die Konvergenzeigenschaften des zweiten Ausdrucks rechts bestimmt, der neu indiziert werden kann, um eine Reihe von allen zu bilden positive Terme beginnend bei n =1.

Jeder Test definiert einen Testparameter (ρ _n ), der das Verhalten dieses Parameters spezifiziert, das benötigt wird, um Konvergenz oder Divergenz herzustellen. Für jeden Test existiert eine schwächere Form des Tests, die stattdessen Beschränkungen auf lim _{n ->} ρ _n auferlegt .

Alle Tests haben Bereiche, in denen sie die Konvergenzeigenschaften von Σa _n nicht beschreiben . Tatsächlich kann kein Konvergenztest die Konvergenzeigenschaften der Reihe vollständig beschreiben. Denn wenn Σa _n konvergent ist, kann eine zweite konvergente Reihe Σb _n gefunden werden, die langsamer konvergiert, dh sie hat die Eigenschaft lim _{n ->} (b _n /a _n ) = ∞. Wenn Σa _n divergent ist, kann außerdem eine zweite divergente Reihe Σb _n gefunden werden, die langsamer divergiert, dh sie hat die Eigenschaft lim _n->∞ (b _n /a _n ) = 0. Konvergenztests verwenden im Wesentlichen den Vergleich Test an einer bestimmten Familie von a _n und scheitern an Folgen, die langsamer konvergieren oder divergieren.

De Morgan-Hierarchie

Augustus De Morgan schlug eine Hierarchie von Ratio-Typ-Tests vor

Bei den nachstehenden Ratio-Testparametern ( ) handelt es sich in der Regel um Terme der Form . Dieser Term kann mit multipliziert werden, um zu ergeben . Dieser Begriff kann den früheren Begriff in der Definition der Testparameter ersetzen und die daraus gezogenen Schlussfolgerungen bleiben gleich. Dementsprechend wird nicht zwischen Referenzen unterschieden, die die eine oder andere Form des Testparameters verwenden. ${\displaystyle \rho_{n}}$${\displaystyle D_{n}a_{n}/a_{n+1}-D_{n+1}}$${\displaystyle a_{n+1}/a_{n}}$${\displaystyle D_{n}-D_{n+1}a_{n+1}/a_{n}}$

1. Verhältnistest von d'Alembert

Der erste Test in der De-Morgan-Hierarchie ist der oben beschriebene Ratio-Test.

2. Raabes Test

Diese Erweiterung geht auf Joseph Ludwig Raabe zurück . Definieren:

${\displaystyle \rho_{n}\equiv n\left({\frac {a_{n}}{a_{n+1}}}-1\right)}$

(und einige zusätzliche Begriffe, siehe Ali, Blackburn, Feld, Duris (keine), Duris2)

Die Serie wird:

• Konvergieren Sie, wenn ein c> 1 existiert, so dass für alle n>N .${\displaystyle \rho_{n}\geq c}$
• Diverge wenn für alle n>N .${\displaystyle \rho_{n}\leq 1}$
• Ansonsten ist der Test nicht aussagekräftig.

Für die Limit-Version wird die Serie:

• Konvergieren Sie, wenn (dies schließt den Fall ρ = ∞ ein)${\displaystyle \rho =\lim_{n\to\infty}\rho_{n}>1}$
• Abweichen, wenn .${\displaystyle \lim_{n\to\infty}\rho_{n}<1}$
• Wenn ρ = 1 ist, ist der Test nicht schlüssig.

Wenn die obige Grenze nicht existiert, kann es möglich sein, Grenzen höher und niedriger zu verwenden. Die Serie wird:

• Konvergieren, wenn ${\displaystyle \liminf_{n\to\infty}\rho_{n}>1}$
• Abweichen, wenn ${\displaystyle \limsup_{n\rightarrow\infty}\rho_{n}<1}$
• Ansonsten ist der Test nicht aussagekräftig.

Nachweis des Raabe-Tests

Wenn wir definieren , müssen wir nicht davon ausgehen, dass der Grenzwert existiert; wenn , dann divergiert, während die Summe konvergiert. ${\displaystyle \rho_{n}\equiv n\left({\frac {a_{n}}{a_{n+1}}}-1\right)}$${\displaystyle \limsup\rho_{n}<1}$${\displaystyle \sum a_{n}}$${\displaystyle \liminf\rho_{n}>1}$

Der Beweis verläuft im Wesentlichen im Vergleich zu . Nehmen wir zunächst an, dass . Natürlich, wenn dann für große , so divergiert die Summe; gehe dann davon aus . Es existiert ein solches für alle , das heißt das . Also , was impliziert, dass für ; da dies zeigt, dass divergiert. ${\displaystyle \sum 1/n^{R}}$${\displaystyle \limsup\rho_{n}<1}$${\displaystyle \limsup\rho_{n}<0}$${\displaystyle a_{n+1}\geq a_{n}}$${\displaystyle n}$${\displaystyle 0\leq\limsup\rho_{n}<1}$${\displaystyle R<1}$${\displaystyle \rho_{n}\leq R}$${\displaystyle n\geq N}$${\displaystyle a_{n}/a_{n+1}\leq \left(1+{\frac{R}{n}}\right)\leq e^{R/n}}$${\displaystyle a_{n+1}\geq a_{n}e^{-R/n}}$${\displaystyle a_{n+1}\geq a_{N}e^{-R(1/N+\dots +1/n)}\geq ca_{N}e^{-R\log(n)}= ca_{N}/n^{R}}$${\displaystyle n\geq N}$${\displaystyle R<1}$${\displaystyle \sum a_{n}}$

Der Beweis der anderen Hälfte ist völlig analog, wobei die meisten Ungleichungen einfach umgekehrt sind. Wir brauchen eine vorläufige Ungleichung, die wir anstelle der oben verwendeten einfachen Ungleichung verwenden können: Fix und . Beachten Sie das . Also ; daher . ${\displaystyle 1+t<e^{t}}$${\displaystyle R}$${\displaystyle N}$${\displaystyle \log \left(1+{\frac {R}{n}}\right)={\frac {R}{n}}+O\left({\frac {1}{n^{2 }}}\rechts)}$${\displaystyle \log \left(\left(1+{\frac{R}{N}}\right)\dots \left(1+{\frac{R}{n}}\right)\right)= R\left({\frac {1}{N}}+\dots +{\frac {1}{n}}\right)+O(1)=R\log(n)+O(1)}$${\displaystyle \left(1+{\frac{R}{N}}\right)\dots \left(1+{\frac{R}{n}}\right)\geq cn^{R}}$

Nehmen wir jetzt an, dass . Wenn wir wie im ersten Absatz argumentieren und die im vorherigen Absatz aufgestellte Ungleichung verwenden, sehen wir, dass es solche gibt, dass für ; da dies zeigt, dass konvergiert. ${\displaystyle \liminf\rho_{n}>1}$${\displaystyle R>1}$${\displaystyle a_{n+1}\leq ca_{N}n^{-R}}$${\displaystyle n\geq N}$${\displaystyle R>1}$${\displaystyle \sum a_{n}}$

3. Bertrands Test

Diese Verlängerung ist Joseph Bertrand und Augustus De Morgan zu verdanken .

Definition:

${\displaystyle \rho_{n}\equiv n\ln n\left({\frac {a_{n}}{a_{n+1}}}-1\right)-\ln n}$

Bertrands Test bestätigt, dass die Serie:

• Konvergieren Sie, wenn ein c>1 existiert, so dass für alle n>N .${\displaystyle \rho_{n}\geq c}$
• Diverge wenn für alle n>N .${\displaystyle \rho_{n}\leq 1}$
• Ansonsten ist der Test nicht aussagekräftig.

Für die Limit-Version wird die Serie:

• Konvergieren Sie, wenn (dies schließt den Fall ρ = ∞ ein)${\displaystyle \rho =\lim_{n\to\infty}\rho_{n}>1}$
• Abweichen, wenn .${\displaystyle \lim_{n\to\infty}\rho_{n}<1}$
• Wenn ρ = 1 ist, ist der Test nicht schlüssig.

Wenn die obige Grenze nicht existiert, kann es möglich sein, Grenzen höher und niedriger zu verwenden. Die Serie wird:

• Konvergieren, wenn ${\displaystyle \liminf\rho_{n}>1}$
• Abweichen, wenn ${\displaystyle \limsup\rho_{n}<1}$
• Ansonsten ist der Test nicht aussagekräftig.

4. Erweiterter Bertrand-Test

Diese Erweiterung ist wahrscheinlich erstmals von Margaret Martin in erschienen. Ein kurzer Beweis auf Basis des Kummer-Tests und ohne technische Annahmen (wie z.

Sei eine ganze Zahl und bezeichne die th Iteration des natürlichen Logarithmus , dh und für jeden , . ${\displaystyle K\geq 1}$${\displaystyle \ln _{(K)}(x)}$${\displaystyle K}$${\displaystyle \ln _{(1)}(x)=\ln(x)}$${\displaystyle 2\leq k\leq K}$${\displaystyle \ln_{(k)}(x)=\ln_{(k-1)}(\ln(x))}$

Angenommen, das Verhältnis , wenn es groß ist, kann in der Form dargestellt werden ${\displaystyle a_{n}/a_{n+1}}$${\displaystyle n}$

${\displaystyle {\frac {a_{n}}{a_{n+1}}}=1+{\frac {1}{n}}+{\frac {1}{n}}\sum _{i =1}^{K-1}{\frac {1}{\prod_{k=1}^{i}\ln _{(k)}(n)}}+{\frac {\rho_{ n}}{n\prod_{k=1}^{K}\ln_{(k)}(n)}},\quad K\geq 1.}$

(Die leere Summe wird als 0 angenommen. Mit reduziert sich der Test auf den Bertrand-Test.) ${\displaystyle K=1}$

Der Wert kann explizit im Formular dargestellt werden ${\displaystyle \rho_{n}}$

${\displaystyle \rho_{n}=n\prod_{k=1}^{K}\ln_{(k)}(n)\left({\frac {a_{n}}{a_{n +1}}}-1\right)-\sum _{j=1}^{K}\prod_{k=1}^{j}\ln _{(K-k+1)}(n) .}$

Der erweiterte Bertrand-Test bestätigt, dass die Serie

• Konvergieren Sie, wenn es ein solches gibt, dass für alle .${\displaystyle c>1}$${\displaystyle \rho_{n}\geq c}$${\displaystyle n>N}$
• Abweichen, wenn für alle .${\displaystyle \rho_{n}\leq 1}$${\displaystyle n>N}$
• Ansonsten ist der Test nicht aussagekräftig.

Für die Limit-Version, die Serie

• Konvergieren, wenn (dies schließt den Fall ein )${\displaystyle \rho =\lim_{n\to\infty}\rho_{n}>1}$${\displaystyle \rho =\infty}$
• Abweichen, wenn .${\displaystyle \lim_{n\to\infty}\rho_{n}<1}$
• Wenn , ist der Test nicht schlüssig.${\displaystyle \rho=1}$

Wenn die obige Grenze nicht existiert, kann es möglich sein, Grenzen höher und niedriger zu verwenden. Die Serie

• Konvergieren, wenn ${\displaystyle \liminf\rho_{n}>1}$
• Abweichen, wenn ${\displaystyle \limsup\rho_{n}<1}$
• Ansonsten ist der Test nicht aussagekräftig.

Für Anwendungen des erweiterten Bertrand-Tests siehe Geburts-Tod-Prozess .

5. Gauss-Test

Diese Erweiterung geht auf Carl Friedrich Gauß zurück .

Angenommen a _n > 0 und r > 1 , wenn eine beschränkte Folge C _{n gefunden werden} kann, so dass für alle n gilt :

${\displaystyle {\frac {a_{n}}{a_{n+1}}}=1+{\frac {\rho }{n}}+{\frac {C_{n}}{n^{r }}}}$

dann wird die serie:

• Konvergieren, wenn ${\displaystyle \rho >1}$
• Abweichen, wenn ${\displaystyle \rho\leq 1}$

6. Kummers Test

Diese Verlängerung geht auf Ernst Kummer zurück .

Sei ζ _n eine Hilfsfolge positiver Konstanten. Definieren

${\displaystyle \rho_{n}\equiv\left(\zeta_{n}{\frac {a_{n}}{a_{n+1}}}-\zeta_{n+1}\right) }$

Kummers Test besagt, dass die Serie:

• Konvergieren Sie, wenn es ein solches gibt, dass für alle n>N gilt. (Beachten Sie, dass dies nicht dasselbe ist wie zu sagen )${\displaystyle c>0}$${\displaystyle \rho_{n}\geq c}$${\displaystyle \rho_{n}>0}$
• Diverge wenn für alle n>N und divergiert.${\displaystyle \rho_{n}\leq 0}$${\displaystyle \sum_{n=1}^{\infty}1/\zeta_{n}}$

Für die Limit-Version wird die Serie:

• Konvergieren Sie, wenn (dies schließt den Fall ρ = ∞ ein)${\displaystyle \lim_{n\to\infty}\rho_{n}>0}$
• Diverge wenn und divergiert.${\displaystyle \lim_{n\to\infty}\rho_{n}<0}$${\displaystyle \sum_{n=1}^{\infty}1/\zeta_{n}}$
• Sonst ist der Test nicht schlüssig

Wenn die obige Grenze nicht existiert, kann es möglich sein, Grenzen höher und niedriger zu verwenden. Die Serie wird

• Konvergieren, wenn ${\displaystyle \liminf_{n\to\infty}\rho_{n}>0}$
• Diverge wenn und divergiert.${\displaystyle \limsup_{n\to\infty}\rho_{n}<0}$${\displaystyle \sum 1/\zeta_{n}}$

Sonderfälle

Alle Tests in der Hierarchie von De Morgan mit Ausnahme des Gauß-Tests können leicht als Sonderfälle des Kummer-Tests angesehen werden:

• Für den Verhältnistest sei ζ _n =1. Dann:

${\displaystyle \rho_{Kummer}=\left({\frac {a_{n}}{a_{n+1}}}-1\right)=1/\rho_{Verhältnis}-1}$

• Für den Raabe-Test sei ζ _n = n. Dann:

${\displaystyle \rho_{Kummer}=\left(n{\frac {a_{n}}{a_{n+1}}}-(n+1)\right)=\rho_{Raabe}-1 }$

• Für den Bertrand-Test sei ζ _n = n ln(n). Dann:

${\displaystyle \rho_{Kummer}=n\ln(n)\left({\frac {a_{n}}{a_{n+1}}}\right)-(n+1)\ln(n +1)}$

Verwenden und approximieren für großes n , das im Vergleich zu den anderen Termen vernachlässigbar ist, kann geschrieben werden: ${\displaystyle \ln(n+1)=\ln(n)+\ln(1+1/n)}$ ${\displaystyle \ln(1+1/n)\rightarrow 1/n}$${\displaystyle \rho_{Kummer}}$

${\displaystyle \rho_{Kummer}=n\ln(n)\left({\frac {a_{n}}{a_{n+1}}}-1\right)-\ln(n)-1 =\rho_{Bertrand}-1}$

• Für den erweiterten Bertrand-Test sei aus der Taylor-Reihenentwicklung für groß die Näherung${\displaystyle \zeta_{n}=n\prod_{k=1}^{K}\ln_{(k)}(n).}$${\displaystyle n}$

${\displaystyle \ln_{(k)}(n+1)=\ln_{(k)}(n)+{\frac {1}{n\prod_{j=1}^{k-1 }\ln _{(j)}(n)}}+O\left({\frac {1}{n^{2}}}\right),}$

wobei angenommen wird, dass das leere Produkt 1 ist. Dann gilt

${\displaystyle \rho_{Kummer}=n\prod_{k=1}^{K}\ln _{(k)}(n){\frac {a_{n}}{a_{n+1} }}-(n+1)\left[\prod_{k=1}^{K}\left(\ln_{(k)}(n)+{\frac {1}{n\prod_{ j=1}^{k-1}\ln_{(j)}(n)}}\right)\right]+o(1)=n\prod_{k=1}^{K}\ln _{(k)}(n)\left({\frac {a_{n}}{a_{n+1}}}-1\right)-\sum_{j=1}^{K}\prod _{k=1}^{j}\ln _{(K-k+1)}(n)-1+o(1).}$

Somit,

${\displaystyle \rho_{Kummer}=\rho_{ExtendedBertrand}-1.}$

Beachten Sie, dass bei diesen vier Tests die Reihe umso langsamer divergiert , je höher sie in der De Morgan-Hierarchie sind . ${\displaystyle 1/\zeta_{n}}$

Nachweis des Kummer-Tests

Wenn dann eine positive Zahl festsetzen . Es gibt eine natürliche Zahl, so dass für jedes${\displaystyle \rho_{n}>0}$${\displaystyle 0<\delta <\rho_{n}}$${\displaystyle N}$${\displaystyle n>N,}$

${\displaystyle \delta\leq\zeta_{n}{\frac{a_{n}}{a_{n+1}}}-\zeta_{n+1}.}$

Da , für jeden${\displaystyle a_{n+1}>0}$${\displaystyle n>N,}$

${\displaystyle 0\leq\delta a_{n+1}\leq\zeta_{n}a_{n}-\zeta_{n+1}a_{n+1}.}$

Insbesondere für alle, was bedeutet, dass ausgehend vom Index die Folge monoton fallend und positiv ist, was insbesondere bedeutet, dass sie nach unten durch 0 begrenzt ist. Daher ist der Grenzwert ${\displaystyle \zeta_{n+1}a_{n+1}\leq\zeta_{n}a_{n}}$${\displaystyle n\geq N}$${\displaystyle N}$${\displaystyle \zeta_{n}a_{n}>0}$

${\displaystyle \lim_{n\to\infty}\zeta_{n}a_{n}=L}$ existiert.

Dies impliziert, dass die positive Teleskopreihe

${\displaystyle \sum_{n=1}^{\infty}\left(\zeta_{n}a_{n}-\zeta_{n+1}a_{n+1}\right)}$ ist konvergent,

und da für alle ${\displaystyle n>N,}$

${\displaystyle \delta a_{n+1}\leq\zeta_{n}a_{n}-\zeta_{n+1}a_{n+1}}$

durch den direkten Vergleichstest für positive Reihen ist die Reihe konvergent. ${\displaystyle \sum_{n=1}^{\infty}\delta a_{n+1}}$

Andererseits, wenn , dann gibt es ein N , das für wächst . Insbesondere gibt es ein für alle , und so divergiert im Vergleich zu . ${\displaystyle \rho <0}$${\displaystyle \zeta_{n}a_{n}}$${\displaystyle n>N}$${\displaystyle \epsilon >0}$${\displaystyle \zeta_{n}a_{n}>\epsilon}$${\displaystyle n>N}$${\displaystyle \sum_{n}a_{n}=\sum_{n}{\frac {a_{n}\zeta_{n}}{\zeta_{n}}}}$${\displaystyle \sum _{n}{\frac {\epsilon }{\zeta_{n}}}}}$

Tongs Modifikation von Kummers Test

Eine neue Version von Kummers Test wurde von Tong entwickelt. Siehe auch für weitere Diskussionen und neue Beweise. Die bereitgestellte Modifikation des Kummerschen Theorems charakterisiert alle positiven Reihen, und die Konvergenz oder Divergenz kann in Form von zwei notwendigen und hinreichenden Bedingungen formuliert werden, eine für die Konvergenz und eine andere für die Divergenz.

• Reihe konvergiert genau dann, wenn es eine positive Folge , gibt , so dass${\displaystyle \sum_{n=1}^{\infty}a_{n}}$${\displaystyle \zeta_{n}}$${\displaystyle n=1,2,\dots}$${\displaystyle \zeta_{n}{\frac {a_{n}}{a_{n+1}}}-\zeta_{n+1}\geq c>0.}$

• Reihe divergiert genau dann, wenn es eine positive Folge , gibt , so dass und${\displaystyle \sum_{n=1}^{\infty}a_{n}}$${\displaystyle \zeta_{n}}$${\displaystyle n=1,2,\dots}$${\displaystyle \zeta_{n}{\frac {a_{n}}{a_{n+1}}}-\zeta_{n+1}\leq 0,}$${\displaystyle \sum _{n=1}^{\infty }{\frac {1}{\zeta_{n}}}=\infty .}$

Alis zweiter Verhältnistest

Ein verfeinerter Verhältnistest ist der zweite Verhältnistest: Für define: ${\displaystyle a_{n}>0}$

${\displaystyle L_{0}\equiv \lim _{n\rightarrow \infty }{\frac {a_{2n}}{a_{n}}}}$

${\displaystyle L_{1}\equiv\lim_{n\rightarrow\infty}{\frac {a_{2n+1}}{a_{n}}}}$

${\displaystyle L\equiv\max(L_{0},L_{1})}$

Beim zweiten Verhältnistest wird die Serie:

• Konvergieren, wenn ${\displaystyle L<{\frac {1}{2}}}$
• Abweichen, wenn ${\displaystyle L>{\frac {1}{2}}}$
• Wenn dann ist der Test nicht schlüssig.${\displaystyle L={\frac {1}{2}}}$

Wenn die oben genannten Grenzen nicht existieren, können die Grenzen höher und niedriger verwendet werden. Definieren:

${\displaystyle L_{0}\equiv\limsup_{n\rightarrow \infty }{\frac {a_{2n}}{a_{n}}}}$		${\displaystyle L_{1}\equiv\limsup_{n\rightarrow\infty}{\frac {a_{2n+1}}{a_{n}}}}$
${\displaystyle \ell _{0}\equiv \liminf _{n\rightarrow \infty }{\frac {a_{2n}}{a_{n}}}}$		${\displaystyle \ell_{1}\equiv\liminf_{n\rightarrow\infty}{\frac {a_{2n+1}}{a_{n}}}}$
${\displaystyle L\equiv\max(L_{0},L_{1})}$		${\displaystyle \ell \equiv \min(\ell_{0},\ell_{1})}$

Dann wird die Serie:

• Konvergieren, wenn ${\displaystyle L<{\frac {1}{2}}}$
• Abweichen, wenn ${\displaystyle \ell >{\frac {1}{2}}}$
• Wenn dann ist der Test nicht schlüssig.${\displaystyle \ell \leq {\frac {1}{2}}\leq L}$

Alis Verhältnistest${\displaystyle m}$

Dieser Test ist eine direkte Erweiterung des zweiten Verhältnistests. Für und positiv definieren: ${\displaystyle 0\leq k\leq m-1,}$${\displaystyle a_{n}}$

${\displaystyle L_{k}\equiv\lim_{n\rightarrow\infty}{\frac {a_{mn+k}}{a_{n}}}}$

${\displaystyle L\equiv\max(L_{0},L_{1},\ldots,L_{m-1})}$

Beim th Verhältnistest wird die Serie: ${\displaystyle m}$

• Konvergieren, wenn ${\displaystyle L<{\frac {1}{m}}}$
• Abweichen, wenn ${\displaystyle L>{\frac {1}{m}}}$
• Wenn dann ist der Test nicht schlüssig.${\displaystyle L={\frac {1}{m}}}$

Wenn die oben genannten Grenzen nicht existieren, können die Grenzen höher und niedriger verwendet werden. Für definieren: ${\displaystyle 0\leq k\leq m-1}$

${\displaystyle L_{k}\equiv\limsup_{n\rightarrow\infty}{\frac {a_{mn+k}}{a_{n}}}}$
${\displaystyle \ell_{k}\equiv \liminf_{n\rightarrow \infty }{\frac {a_{mn+k}}{a_{n}}}}$
${\displaystyle L\equiv\max(L_{0},L_{1},\ldots,L_{m-1})}$		${\displaystyle \ell\equiv\min(\ell_{0},\ell_{1},\ldots,\ell_{m-1})}$

Dann wird die Serie:

• Konvergieren, wenn ${\displaystyle L<{\frac {1}{m}}}$
• Abweichen, wenn ${\displaystyle \ell >{\frac {1}{m}}}$
• Wenn , ist der Test nicht schlüssig.${\displaystyle \ell \leq {\frac {1}{m}}\leq L}$

Ali-Deutsche Cohen -Verhältnistest${\displaystyle\varphi}$

Dieser Test ist eine Erweiterung des th-Ratio-Tests. ${\displaystyle m}$

Angenommen, die Folge ist eine positiv fallende Folge. ${\displaystyle a_{n}}$

Seien Sie ein solches, das existiert. Bezeichne und nimm an . ${\displaystyle \varphi :\mathbb {Z} ^{+}\to \mathbb {Z} ^{+}}$${\displaystyle \lim_{n\to \infty }{\frac {n}{\varphi(n)}}}$${\displaystyle \alpha =\lim_{n\to\infty }{\frac {n}{\varphi(n)}}}$${\displaystyle 0<\alpha <1}$

Gehe auch davon aus ${\displaystyle \lim_{n\to\infty }{\frac {a_{\varphi(n)}}{a_{n}}}=L.}$

Dann wird die Serie:

• Konvergieren, wenn ${\displaystyle L<\alpha}$
• Abweichen, wenn ${\displaystyle \ell >\alpha}$
• Wenn , ist der Test nicht schlüssig.${\displaystyle L=\alpha}$

Siehe auch

• Wurzeltest
• Konvergenzradius

Fußnoten

Verweise

• d'Alembert, J. (1768), Opuscules , V , S. 171–183.
• Apostol, Tom M. (1974), Mathematische Analyse (2. Aufl.), Addison-Wesley , ISBN 978-0-201-00288-1: §8.14.
• Knopp, Konrad (1956), Infinite Sequences and Series , New York: Dover Publications, Bibcode : 1956iss..book.....K , ISBN 978-0-486-60153-3: §3.3, 5.4.
• Rudin, Walter (1976), Prinzipien der mathematischen Analyse (3. Aufl.), New York: McGraw-Hill, Inc., ISBN 978-0-07-054235-8: §3.34.
• "Bertrand-Kriterium" , Enzyklopädie der Mathematik , EMS Press , 2001 [1994]
• "Gauss-Kriterium" , Encyclopedia of Mathematics , EMS Press , 2001 [1994]
• "Kummer-Kriterium" , Enzyklopädie der Mathematik , EMS Press , 2001 [1994]
• Watson, GN; Whittaker, ET (1963), A Course in Modern Analysis (4. Aufl.), Cambridge University Press, ISBN 978-0-521-58807-2: §2.36, 2.37.