Eulersche Totient-Funktion - Euler's totient function

Die ersten tausend Werte von

φ (n)

. Die Punkte auf der oberen Linie stellen

φ (p) dar,

wenn

p

eine Primzahl ist, die

p - 1 ist.

In der Zahlentheorie , Eulersche Phi-Funktion zählt die positiven ganzen Zahlen bis zu einer bestimmten ganzen Zahl $n$ , die relativ prim zu $n$ . Es wird mit dem griechischen Buchstaben phi als oder geschrieben und kann auch Eulers Phi-Funktion genannt werden . Mit anderen Worten, es ist die Zahl der ganzen Zahlen $k$ im Bereich $1 \leq$ $k$ $\leq$ $n,$ für die der größte gemeinsame Teiler $gcd($ $n$ $,$ $k$ $)$ gleich 1 ist. Die ganzen Zahlen $k$ dieser Form werden manchmal als Totalative von $n . bezeichnet$ . ${\displaystyle\varphi(n)}$ $\phi(n)$

Zum Beispiel sind die Totative von $n = 9$ die sechs Zahlen 1, 2, 4, 5, 7 und 8. Sie sind alle relativ prim zu 9, aber die anderen drei Zahlen in diesem Bereich, 3, 6 und 9 sind es nicht , da $gcd(9, 3) = gcd(9, 6) = 3$ und $gcd(9, 9) = 9$ . Daher $φ 6 = (9)$ . Als weiteres Beispiel gilt $φ (1) = 1,$ da für $n = 1$ die einzige ganze Zahl im Bereich von 1 bis $n$ 1 selbst ist und $gcd(1, 1) = 1$ .

Eulersche Totientenfunktion ist eine multiplikative Funktion , was bedeutet , dass , wenn zwei Zahlen $m$ und $n$ relativ prim ist , dann $φ (Mn) = φ (m) , φ (n)$ . Diese Funktion gibt die Ordnung der multiplikativen Gruppe von ganzen Zahlen modulo $n$ (die Gruppe der Einheiten des Rings ) an. Es wird auch zur Definition des RSA-Verschlüsselungssystems verwendet . $\mathbb{Z} /n\mathbb{Z}$

Geschichte, Terminologie und Notation

Leonhard Euler führte die Funktion 1763 ein. Allerdings wählte er damals noch kein konkretes Symbol, um sie zu kennzeichnen. In einer Veröffentlichung von 1784 untersuchte Euler die Funktion weiter und wählte den griechischen Buchstaben $π$ , um sie zu bezeichnen: Er schrieb $πD$ für "die Vielzahl der Zahlen kleiner als $D$ , und die keinen gemeinsamen Teiler damit haben". Diese Definition weicht von der aktuellen Definition für die Totient-Funktion bei $D = 1 ab$ , ist aber ansonsten gleich. Die heute übliche Notation $φ (A)$ stammt aus Gauss ' Abhandlung Disquisitiones Arithmeticae von 1801 , obwohl Gauß das Argument nicht in Klammern $umschloss$ und A schrieb . Daher wird sie oft als Eulersche Phi-Funktion oder einfach als Phi-Funktion bezeichnet .

Im Jahr 1879 prägte JJ Sylvester den Begriff Totient für diese Funktion, daher wird er auch als Euler-Totient-Funktion , Euler-Totient oder Euler-Totient bezeichnet . Jordans Totient ist eine Verallgemeinerung von Eulers.

Der Kototient von $n$ ist definiert als $n - φ (n)$ . Es zählt die Anzahl der positiven ganzen Zahlen kleiner oder gleich $n$ , die mindestens einen Primfaktor mit $n gemeinsam haben$ .

Berechnung der Eulerschen Totient-Funktion

Es gibt mehrere Formeln zur Berechnung von $φ (n)$ .

Produktformel von Euler

Es sagt aus

\varphi(n)=n\prod_{p\mid n}\left(1-{\frac {1}{p}}\right),

wobei das Produkt über den verschiedenen Primzahlen liegt, die $n$ teilen . (Notation siehe Arithmetische Funktion .)

Eine äquivalente Formulierung für , wobei die verschiedenen Primzahlen n teilen , lautet: $n=p_{1}^{k_{1}}p_{2}^{k_{2}}\cdots p_{r}^{k_{r}}$ $p_{1},p_{2},\ldots ,p_{r}$

\varphi(n)=p_{1}^{k_{1}-1}(p_{1}{-}1)\,p_{2}^{k_{2}-1}(p_{ 2}{-}1)\cdots p_{r}^{k_{r}-1}(p_{r}{-}1).

Der Beweis dieser Formeln hängt von zwei wichtigen Tatsachen ab.

Phi ist eine multiplikative Funktion

Dies bedeutet, dass wenn $gcd(m, n) = 1 ist$ , dann $φ (m) φ (n) = φ (mn)$ . Proof Umriss: Let $A$ , $B$ , $C$ die Sätze von positiven ganzen Zahlen sein , die sind coprime auf und kleiner als $m$ , $n$ , $mn$ jeweils, so dass $| A | = φ (m)$ usw. Dann gibt es eine Bijektion zwischen $A \times B$ und $C$ nach dem chinesischen Restsatz .

Wert von phi für ein Primzahlargument

Wenn $p$ eine Primzahl ist und $k 1$ , dann

\varphi\left(p^{k}\right)=p^{k}-p^{k-1}=p^{k-1}(p-1)=p^{k}\ left(1-{\tfrac {1}{p}}\right).

Beweis : Da $p$ eine Primzahl ist , die einzig möglichen Werte von $gcd (p k, m)$ sind $1, p, p 2, ..., p k$ , und der einzige Weg , um $gcd (p k, m)> 1$ ist, wenn $m$ ein Vielfaches von $p ist$ , dh $m = p, 2 p, 3 p, ..., p k - 1 p = p k$ , und es gibt $p k - 1$ solcher Vielfachen kleiner als $p k$ . Daher sind die anderen $p k - p k - 1$ Zahlen alle relativ prim zu $p k$ .

Beweis der Eulerschen Produktformel

Der Hauptsatz der Arithmetik besagt , dass wenn $n > 1$ ist ein einzigartiger Ausdruck , wo $p$ $1$ $<$ $p$ $2$ $<... <$ $p$ $r$ sind Primzahlen und jeder $k$ $i$ $\geq 1$ . (Der Fall $n$ $= 1$ entspricht dem leeren Produkt.) Wiederholtes Verwenden der Multiplikativeigenschaft von $φ$ und die Formel für $φ$ $($ $p$ $k$ $)$ ergibt $n=p_{1}^{k_{1}}p_{2}^{k_{2}}\cdots p_{r}^{k_{r}},$

{\begin{array}{rcl}\varphi (n)&=&\varphi (p_{1}^{k_{1}})\,\varphi (p_{2}^{k_{2} })\cdots \varphi (p_{r}^{k_{r}})\\[.1em]&=&p_{1}^{k_{1}-1}(p_{1}-1)\, p_{2}^{k_{2}-1}(p_{2}-1)\cdots p_{r}^{k_{r}-1}(p_{r}-1)\\[.1em] &=&p_{1}^{k_{1}}\left(1-{\frac {1}{p_{1}}}\right)p_{2}^{k_{2}}\left(1- {\frac {1}{p_{2}}}\right)\cdots p_{r}^{k_{r}}\left(1-{\frac {1}{p_{r}}}\right) \\[.1em]&=&p_{1}^{k_{1}}p_{2}^{k_{2}}\cdots p_{r}^{k_{r}}\left(1-{\ frac {1}{p_{1}}}\right)\left(1-{\frac {1}{p_{2}}}\right)\cdots \left(1-{\frac {1}{p_ {r}}}\right)\\[.1em]&=&n\left(1-{\frac {1}{p_{1}}}\right)\left(1-{\frac {1}{ p_{2}}}\right)\cdots \left(1-{\frac {1}{p_{r}}}\right).\end{array}}

Dies ergibt beide Versionen der Euler-Produktformel.

Ein alternativer Beweis, der die multiplikative Eigenschaft nicht erfordert, verwendet stattdessen das Einschluss-Ausschluss-Prinzip, das auf die Menge angewendet wird und die Mengen von ganzen Zahlen ausschließt, die durch die Primteiler teilbar sind. $\{1,2,\ldots,n\}$

Beispiel

\varphi (20)=\varphi (2^{2}5)=20\,(1-{\tfrac {1}{2}})\,(1-{\tfrac {1}{5 }})=20\cdot {\tfrac {1}{2}}\cdot {\tfrac {4}{5}}=8.

In Worten: die verschiedenen Primfaktoren von 20 sind 2 und 5; die Hälfte der zwanzig ganzen Zahlen von 1 bis 20 ist durch 2 teilbar, so dass zehn übrig bleibt; ein Fünftel davon ist durch 5 teilbar, so dass acht Zahlen zu 20 teilerfremd sind; das sind: 1, 3, 7, 9, 11, 13, 17, 19.

Die alternative Formel verwendet nur ganze Zahlen:

\varphi (20)=\varphi (2^{2}5^{1})=2^{2-1}(2{-}1)\,5^{1-1}(5{ -}1)=2\cdot 1\cdot 1\cdot 4=8.

Fourier-Transformation

Der Totient ist die diskrete Fourier-Transformation des gcd , ausgewertet bei 1. Sei

{\mathcal{F}}\{\mathbf{x}\}[m]=\sum\limits_{k=1}^{n}x_{k}\cdot e^{{-2\ pi i}{\frac {mk}{n}}}

wobei $x k = gcd(k, n)$ für $k \in {1, ..., n}$ . Dann

\varphi(n)={\mathcal{F}}\{\mathbf{x}\}[1]=\sum\limits_{k=1}^{n}\gcd(k,n) e^{-2\pi i{\frac {k}{n}}}.

Der eigentliche Teil dieser Formel ist

\varphi(n)=\sum\limits_{k=1}^{n}\gcd(k,n)\cos {\tfrac {2\pi k}{n}}.

Verwenden Sie zum Beispiel und : $\cos {\tfrac {\pi}{5}}={\tfrac {{\sqrt {5}}+1}{4}}$ $\cos {\tfrac {2\pi }{5}}={\tfrac {{\sqrt {5}}-1}{4}}$

{\begin{array}{rcl}\varphi (10)&=&\gcd(1,10)\cos {\tfrac {2\pi}{10}}+\gcd(2,10)\ cos {\tfrac {4\pi }{10}}+\gcd(3,10)\cos {\tfrac {6\pi }{10}}+\cdots +\gcd(10,10)\cos {\ tfrac {20\pi }{10}}\\&=&1\cdot ({\tfrac {{\sqrt {5}}+1}{4}})+2\cdot ({\tfrac {{\sqrt { 5}}-1}{4}})+1\cdot (-{\tfrac {{\sqrt {5}}-1}{4}})+2\cdot (-{\tfrac {{\sqrt { 5}}+1}{4}})+5\cdot (-1)\\&&+\ 2\cdot (-{\tfrac {{\sqrt {5}}+1}{4}})+1 \cdot (-{\tfrac {{\sqrt {5}}-1}{4}})+2\cdot ({\tfrac {{\sqrt {5}}-1}{4}})+1\ cdot ({\tfrac {{\sqrt {5}}+1}{4}})+10\cdot (1)\\&=&4.\end{array}}

Im Gegensatz zum Euler-Produkt und der Divisorsummenformel erfordert diese keine Kenntnis der Faktoren von

n

. Es beinhaltet jedoch die Berechnung des größten gemeinsamen Teilers von

n

und jeder positiven ganzen Zahl kleiner als

n

, was ohnehin ausreicht, um die Faktorisierung bereitzustellen.

Teilersumme

Das von Gauss gegründete Grundstück, das

\sum_{d\mid n}\varphi(d)=n,

wobei die Summe über alle positiven Teiler $d$ von $n ist$ , kann auf verschiedene Weise bewiesen werden. (Siehe Arithmetische Funktion für Notationskonventionen.)

Ein Beweis ist, dass $φ (d)$ auch gleich der Anzahl möglicher Generatoren der zyklischen Gruppe $C d ist$ ; insbesondere, wenn $C d = ⟨ g ⟩$ mit $g d = 1 ist$ , dann ist $g k$ ein Generator für jede $k$ Koprime zu $d$ . Da jedes Element von $C n$ eine zyklische Untergruppe erzeugt und alle Untergruppen $C d \subseteq C n$ durch genau $φ (d)$ Elemente von $C n erzeugt werden$ , folgt die Formel. Äquivalent kann die Formel durch das gleiche Argument abgeleitet werden, das auf die multiplikative Gruppe der $n-$ ten Einheitswurzeln und der primitiven $d-$ ten Einheitswurzeln angewendet wird .

Die Formel lässt sich auch aus der elementaren Arithmetik ableiten. Sei zum Beispiel $n = 20$ und betrachte die positiven Brüche bis 1 mit Nenner 20:

{\tfrac {1}{20}},\,{\tfrac {2}{20}},\,{\tfrac {3}{20}},\,{\tfrac {4}{20 }},\,{\tfrac {5}{20}},\,{\tfrac {6}{20}},\,{\tfrac {7}{20}},\,{\tfrac {8} {20}},\,{\tfrac {9}{20}},\,{\tfrac {10}{20}},\,{\tfrac {11}{20}},\,{\tfrac { 12}{20}},\,{\tfrac {13}{20}},\,{\tfrac {14}{20}},\,{\tfrac {15}{20}},\,{\ tfrac {16}{20}},\,{\tfrac {17}{20}},\,{\tfrac {18}{20}},\,{\tfrac {19}{20}},\, {\tfrac {20}{20}}.

Bringen Sie sie in die niedrigsten Begriffe:

{\tfrac {1}{20}},\,{\tfrac {1}{10}},\,{\tfrac {3}{20}},\,{\tfrac {1}{5 }},\,{\tfrac {1}{4}},\,{\tfrac {3}{10}},\,{\tfrac {7}{20}},\,{\tfrac {2} {5}},\,{\tfrac {9}{20}},\,{\tfrac {1}{2}},\,{\tfrac {11}{20}},\,{\tfrac { 3}{5}},\,{\tfrac {13}{20}},\,{\tfrac {7}{10}},\,{\tfrac {3}{4}},\,{\ tfrac {4}{5}},\,{\tfrac {17}{20}},\,{\tfrac {9}{10}},\,{\tfrac {19}{20}},\, {\tfrac {1}{1}}

Diese zwanzig Brüche sind alle positiv k/D≤ 1, deren Nenner die Teiler $d = 1, 2, 4, 5, 10, 20 sind$ . Die Brüche mit 20 als Nenner sind solche mit Zählern teilerfremd zu 20, nämlich1/20, 3/20, 7/20, 9/20, 11/20, 13/20, 17/20, 19/20; per Definition sind dies $φ (20)$ Brüche. In ähnlicher Weise gibt es $φ (10)$ Brüche mit Nenner 10 und $φ (5)$ Brüche mit Nenner 5 usw. Somit wird die Menge von zwanzig Brüchen in Teilmengen der Größe $φ (d)$ für jedes $d$ geteilt, das 20 teilt. Ein ähnliches Argument gilt für jedes n.

Auf die Divisorsummenformel angewendete Möbius-Inversion ergibt

\varphi(n)=\sum_{d\mid n}\mu\left(d\right)\cdot {\frac {n}{d}}=n\sum_{d\mid n} {\frac{\mu(d)}{d}},

wobei $μ$ die Möbius-Funktion ist , die durch und für jede Primzahl $p$ und $k$ $\geq 1$ definierte multiplikative Funktion . Diese Formel kann auch aus der Produktformel durch Multiplikation abgeleitet werden , um zu erhalten $\mu(p)=-1$ $\mu(p^{k})=0$ ${\textstyle \prod_{p\mid n}(1-{\frac {1}{p}})}$ ${\textstyle \sum _{d\mid n}{\frac {\mu(d)}{d}}.}$

Ein Beispiel:

{\begin{ausgerichtet}\varphi (20)&=\mu (1)\cdot 20+\mu (2)\cdot 10+\mu (4)\cdot 5+\mu (5)\cdot 4+\mu (10)\cdot 2+\mu (20)\cdot 1\\[.5em]&=1\cdot 20-1\cdot 10+0\cdot 5-1\cdot 4+1\cdot 2+0\cdot 1=8.\end{ausgerichtet}}

Einige Werte

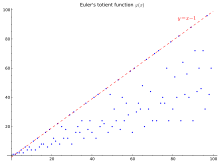
Die ersten 100 Werte (Sequenz A000010 im OEIS ) sind in der folgenden Tabelle und Grafik dargestellt:

Grafik der ersten 100 Werte

$φ (n)$ für $1 \leq n \leq 100$
+	1	2	3	4	5	6	7	8	9	10
0	1	1	2	2	4	2	6	4	6	4
10	10	4	12	6	8	8	16	6	18	8
20	12	10	22	8	20	12	18	12	28	8
30	30	16	20	16	24	12	36	18	24	16
40	40	12	42	20	24	22	46	16	42	20
50	32	24	52	18	40	24	36	28	58	16
60	60	30	36	32	48	20	66	32	44	24
70	70	24	72	36	40	36	60	24	78	32
80	54	40	82	24	64	42	56	40	88	24
90	72	44	60	46	72	32	96	42	60	40

Im rechten Graphen ist die obere Linie $y = n - 1$ eine obere Schranke, die für alle $n$ außer eins gültig ist und genau dann erreicht wird, wenn $n$ eine Primzahl ist. Eine einfache untere Schranke ist , die ziemlich locker ist: Tatsächlich ist die untere Grenze des Graphen proportional zu $\varphi(n)\geq {\sqrt {n/2}}$ $n / log log nr$ .

Satz von Euler

Dies besagt , dass , wenn $ein$ und $n$ sind relativ prim dann

a^{\varphi(n)}\equiv 1\mod n.

Der Spezialfall, in dem $n$ eine Primzahl ist, wird als kleiner Satz von Fermat bezeichnet .

Dies folgt aus dem Satz von Lagrange und der Tatsache, dass $φ (n)$ die Ordnung der multiplikativen Gruppe ganzer Zahlen modulo $n ist$ .

Das RSA-Kryptosystem basiert auf diesem Theorem: Es impliziert, dass die Inverse der Funktion $a \mapsto a e mod n$ , wobei $e$ der (öffentliche) Verschlüsselungsexponent ist, die Funktion $b \mapsto b d mod n ist$ , wobei $d$ , der (private ) Entschlüsselungs Exponent ist die multiplikative inverse von $e$ modulo $φ (n)$ . Die Schwierigkeit, $φ (n)$ zu berechnen, ohne die Faktorisierung von $n zu kennen,$ ist somit die Schwierigkeit, $d zu$ berechnen : Dies ist als RSA-Problem bekannt , das durch Faktorisieren von $n$ gelöst werden kann . Der Besitzer des privaten Schlüssels kennt die Faktorisierung, da ein privater RSA-Schlüssel konstruiert wird, indem $n$ als Produkt zweier (zufällig gewählter) großer Primzahlen $p$ und $q gewählt wird$ . Nur $n$ wird öffentlich bekannt gegeben, und angesichts der Schwierigkeit, große Zahlen zu faktorisieren, haben wir die Garantie, dass niemand sonst die Faktorisierung kennt.

Andere Formeln

$a\mid b\impliest \varphi (a)\mid \varphi (b)$
$n\mid \varphi (a^{n}-1)\quad {\text{for}}a,n>1$
$\varphi (mn)=\varphi (m)\varphi (n)\cdot {\frac {d}{\varphi (d)}}\quad {\text{wo }}d=\operatorname {gcd } (m,n)$ $\varphi (mn)=\varphi (m)\varphi (n)\cdot {\frac {d}{\varphi (d)}}\quad {\text{wo }}d=\operatorname {gcd } (m,n)$
Beachten Sie die Sonderfälle
- $\varphi (2m)={\begin{cases}2\varphi (m)&{\text{ if }}m{\text{ gerade}}\\\varphi (m)&{\text{ wenn }}m{\text{ ungerade}}\end{cases}}$
- $\varphi\left(n^{m}\right)=n^{m-1}\varphi(n)$
$\varphi (\operatorname {lcm} (m,n))\cdot \varphi (\operatorname {gcd} (m,n))=\varphi (m)\cdot \varphi (n)$ $\varphi (\operatorname {lcm} (m,n))\cdot \varphi (\operatorname {gcd} (m,n))=\varphi (m)\cdot \varphi (n)$
Vergleichen Sie dies mit der Formel
- $\operatorname {lcm} (m,n)\cdot \operatorname {gcd} (m,n)=m\cdot n$
(Siehe kleinstes gemeinsames Vielfaches .)
$φ (n)$ ist gerade für $n 3$ . Außerdem, wenn $n$ hat $r$ verschiedene ungerade Primfaktoren $2 r | φ (n)$
Für jeden $a > 1$ und $n > 6$ , so dass $4 ∤ n$ existiert ein $l \geq 2 n$ , so daß $l | φ (a n - 1)$ .
${\frac {\varphi (n)}{n}}={\frac {\varphi (\operatorname {rad} (n))}{\operatorname {rad} (n)}}$
wobei $rad(n)$ der Rest von $n ist$ (das Produkt aller verschiedenen Primzahlen, die $n$ teilen ).
$\sum_{d\mid n}{\frac {\mu^{2}(d)}{\varphi(d)}}={\frac {n}{\varphi(n)}}$
$\sum _{1\leq k\leq n \atop (k,n)=1}\!\!k={\tfrac {1}{2}}n\varphi (n)\quad {\ text{for }}n>1$
$\sum_{k=1}^{n}\varphi(k)={\tfrac {1}{2}}\left(1+\sum_{k=1}^{n}\mu (k)\left\lfloor {\frac{n}{k}}\right\rfloor^{2}\right)={\frac{3}{\pi^{2}}}n^{2}+ O\left(n(\log n)^{\frac {2}{3}}(\log\log n)^{\frac {4}{3}}\right)$ ( zitiert in)
$\sum_{k=1}^{n}{\frac {\varphi(k)}{k}}=\sum_{k=1}^{n}{\frac {\mu(k )}{k}}\left\lfloor {\frac {n}{k}}\right\rfloor ={\frac {6}{\pi^{2}}}n+O\left((\log n )^{\frac {2}{3}}(\log\log n)^{\frac {4}{3}}\right)$
$\sum_{k=1}^{n}{\frac {k}{\varphi(k)}}={\frac {315\,\zeta (3)}{2\pi ^{4 }}}n-{\frac {\log n}{2}}+O\left((\log n)^{\frac {2}{3}}\right)$
$\sum _{k=1}^{n}{\frac {1}{\varphi (k)}}={\frac {315\,\zeta (3)}{2\pi ^{4 }}}\left(\log n+\gamma -\sum_{p{\text{ prime}}}{\frac {\log p}{p^{2}-p+1}}\right)+O \left({\frac {(\log n)^{\frac {2}{3}}}{n}}\right)$
(wobei $γ$ die Euler-Mascheroni-Konstante ist ).
$\sum _{\stackrel {1\leq k\leq n}{\operatorname {gcd} (k,m)=1}}\!\!\!\!1=n{\frac {\varphi (m)}{m}}+O\left(2^{\omega (m)}\right)$
wobei $m > 1$ ist eine positive ganze Zahl ist , und $ω (m)$ ist die Anzahl der verschiedenen Primfaktoren von $m$ .

Menons Identität

1965 bewies P. Kesava Menon

\sum _{\stackrel {1\leq k\leq n}{\gcd(k,n)=1}}\!\!\!\!\gcd(k-1,n)=\varphi (n)d(n),

wobei $d (n) = σ 0 (n)$ ist die Anzahl der Teiler von $n$ .

Formeln mit dem Goldenen Schnitt

Schneider fand ein Identitätspaar, das die Totient-Funktion, den Goldenen Schnitt und die Möbius-Funktion $μ (n) verbindet$ . In diesem Abschnitt ist $φ (n)$ die Totient-Funktion und $ϕ = 1 + \sqrt 5 / 2 = 1,618...$ ist der Goldene Schnitt.

Sie sind:

\phi =-\sum_{k=1}^{\infty }{\frac {\varphi (k)}{k}}\log \left(1-{\frac {1}{\phi ^{k}}}\right)

und

{\frac {1}{\phi}}=-\sum _{k=1}^{\infty }{\frac {\mu(k)}{k}}\log \left(1- {\frac{1}{\phi^{k}}}\right).

Subtrahieren ergibt

\sum _{k=1}^{\infty }{\frac {\mu(k)-\varphi(k)}{k}}\log\left(1-{\frac {1}{ \phi^{k}}}\right)=1.

Die Anwendung der Exponentialfunktion auf beide Seiten der vorhergehenden Identität ergibt eine unendliche Produktformel für $e$ :

e=\prod_{k=1}^{\infty}\left(1-{\frac {1}{\phi^{k}}}\right)\!\!^{\frac { \mu(k)-\varphi(k)}{k}}.

Der Beweis basiert auf den beiden Formeln

{\begin{ausgerichtet}\sum _{k=1}^{\infty }{\frac {\varphi (k)}{k}}\left(-\log \left(1-x^{ k}\right)\right)&={\frac {x}{1-x}}\\{\text{and}}\;\sum _{k=1}^{\infty }{\frac { \mu(k)}{k}}\left(-\log \left(1-x^{k}\right)\right)&=x,\qquad \quad {\text{for }}0<x <1.\end{ausgerichtet}}

Generieren von Funktionen

Die Dirichlet-Reihe für $φ (n)$ kann im Sinne der Riemannschen Zetafunktion geschrieben werden als:

\sum _{n=1}^{\infty }{\frac {\varphi (n)}{n^{s}}}={\frac {\zeta (s-1)}{\zeta (S)}}.

Die Erzeugungsfunktion der Lambert-Reihe ist

\sum _{n=1}^{\infty }{\frac {\varphi(n)q^{n}}{1-q^{n}}}={\frac {q}{( 1-q)^{2}}}

die für $| .$ konvergiert $q$ $|$ $<1$ .

Beides wird durch elementare Reihenmanipulationen und die Formeln für $φ (n)$ bewiesen .

Wachstumsrate

In den Worten von Hardy & Wright ist die Reihenfolge von $φ (n)$ „immer ‚fast $n$ ‘“.

Zuerst

\lim\sup {\frac {\varphi(n)}{n}}=1,

aber da n gegen unendlich geht, für alle $δ > 0$

{\frac {\varphi(n)}{n^{1-\delta}}}\rightarrow\infty.

Diese beiden Formeln können mit wenig mehr als die Formeln für beweisen $φ (n)$ und der Divisor Summenfunktion $σ (n)$ .

Tatsächlich wird beim Beweis der zweiten Formel die Ungleichung

{\frac {6}{\pi^{2}}}<{\frac {\varphi (n)\sigma (n)}{n^{2}}}<1,

gilt für $n > 1$ , ist bewiesen.

Wir haben auch

\lim\inf {\frac {\varphi(n)}{n}}\log\log n=e^{-\gamma}.

Hier ist $γ$ die Eulersche Konstante , $γ = 0.577215665...$ , also $e γ = 1.7810724...$ und $e - γ = 0.56145948...$ .

Um dies zu beweisen bedarf es nicht ganz des Primzahlensatzes . Da $log log n$ gegen unendlich geht, zeigt diese Formel, dass

\lim\inf {\frac {\varphi(n)}{n}}=0.

Tatsächlich ist mehr wahr.

\varphi(n)>{\frac {n}{e^{\gamma}\;\log\log n+{\frac {3}{\log\log n}}}}\quad {\text {für }}n>2

und

\varphi(n)<{\frac {n}{e^{\gamma}\log\log n}}\quad {\text{für unendlich viele }}n.

Die zweite Ungleichung wurde von Jean-Louis Nicolas gezeigt . Ribenboim sagt: "Die Beweismethode ist insofern interessant, als die Ungleichung erstens unter der Annahme, dass die Riemannsche Hypothese wahr ist, zweitens unter der gegenteiligen Annahme gezeigt wird."

Für die durchschnittliche Bestellung haben wir

\varphi (1)+\varphi (2)+\cdots +\varphi(n)={\frac {3n^{2}}{\pi^{2}}}+O\left(n( \log n)^{\frac {2}{3}}(\log \log n)^{\frac {4}{3}}\right)\quad {\text{as }}n\rightarrow \infty ,

aufgrund von Arnold Walfisz , dessen Beweis die Schätzungen von Exponentialsummen aufgrund von IM Vinogradov und NM Korobov ausnutzt (dies ist derzeit die bekannteste Schätzung dieser Art). Das "große $O$ " steht für eine Größe, die durch eine Konstante mal der Funktion von $n$ innerhalb der Klammern begrenzt ist (die klein ist im Vergleich zu $n 2$ ).

Dieses Ergebnis kann verwendet werden, um zu beweisen, dass die Wahrscheinlichkeit, dass zwei zufällig ausgewählte Zahlen relativ prim sind, 6/ $π$ ².

Verhältnis aufeinanderfolgender Werte

1950 bewies Somayajulu

{\begin{ausgerichtet}\lim\inf {\frac {\varphi (n+1)}{\varphi (n)}}&=0\quad {\text{and}}\\[5px] \lim \sup {\frac {\varphi (n+1)}{\varphi (n)}}&=\infty .\end{ausgerichtet}}

1954 verstärkten Schinzel und Sierpiński dies und bewiesen, dass das Set

\left\{{\frac {\varphi (n+1)}{\varphi (n)}},\;\;n=1,2,\ldots \right\}

ist dicht in den positiven reellen Zahlen. Sie haben auch bewiesen, dass die Menge

\left\{{\frac {\varphi(n)}{n}},\;\;n=1,2,\ldots \right\}

ist im Intervall (0,1) dicht.

Totient-Zahlen

A totient Zahl ist ein Wert , der die Eulersche Totientenfunktion: Das heißt, ein $m$ , für die es mindestens ein $n$ für die $φ (n) = m$ . Die Wertigkeit oder Multiplizität einer Gesamtzahl $m$ ist die Anzahl der Lösungen dieser Gleichung. Ein Nichttotient ist eine natürliche Zahl, die keine totiente Zahl ist. Jede ungerade ganze Zahl, die 1 überschreitet, ist trivialerweise ein Nichttotient. Es gibt auch unendlich viele gerade Nichttotienten, und tatsächlich hat jede positive ganze Zahl ein Vielfaches, das ein gerader Nichttotient ist.

Die Anzahl der Summenzahlen bis zu einem gegebenen Grenzwert $x$ ist

{\frac {x}{\log x}}e^{{\big (}C+o(1){\big)}(\log\log\log x)^{2}}

für eine Konstante $C = 0,8178146...$ .

Wenn dementsprechend Multiplizität gezählt, bis die Anzahl der totient Zahlen auf einen gegebenen Grenzwert $x$ ist

{\Big\vert}\{n:\varphi(n)\leq x\}{\Big\vert}={\frac {\zeta (2)\zeta (3)}{\zeta (6 )}}\cdot x+R(x)

wobei der Fehlerterm $R$ höchstens von Ordnung ist $x / (log x) k$ für jedes positive $k$ .

Es ist bekannt , dass die Vielzahl von $m$ überschreitet $m δ$ unendlich oft für jeden $δ <0,55655$ .

Fords Theorem

Ford (1999) bewies, dass es für jede ganze Zahl $k \geq 2$ eine totiente Zahl $m$ der Vielfachheit $k$ gibt, dh für die die Gleichung $φ (n) = m$ genau $k$ Lösungen hat; dieses Ergebnis war zuvor von Wacław Sierpiński vermutet worden , und es war als Folge von Schinzels Hypothese H erhalten worden . Tatsächlich tut jede Vielheit, die auftritt, dies unendlich oft.

Es ist jedoch keine Zahl $m$ mit der Multiplizität $k = 1 bekannt$ . Carmichaels Totient-Funktions-Vermutung ist die Aussage, dass es kein solches $m gibt$ .

Perfekte Totient-Zahlen

Anwendungen

Zyklotomie

Im letzten Abschnitt der Disquisitiones beweist Gauß, dass ein regelmäßiges $n$ -Eck mit Lineal und Zirkel konstruiert werden kann, wenn $φ (n)$ eine Potenz von 2 ist. Wenn $n$ eine Potenz einer ungeraden Primzahl ist, sagt die Formel für den Totient totient kann nur dann eine Zweierpotenz sein, wenn $n$ eine erste Potenz und $n - 1$ eine Zweierpotenz ist . Die Primzahlen, die um eins größer als eine Zweierpotenz sind, werden Fermat-Primzahlen genannt , und nur fünf sind bekannt: 3, 5, 17, 257 und 65537. Fermat und Gauss wussten davon. Ob es noch mehr gibt, konnte niemand beweisen.

Ein reguläres $n$ -Eck hat also eine Lineal-und-Kompass-Konstruktion, wenn n ein Produkt verschiedener Fermat-Primzahlen und einer beliebigen Potenz von 2 ist. Die ersten paar solcher $n$ sind

2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30, 32, 34, 40,... (Sequenz A003401 im OEIS ).

Das RSA-Kryptosystem

Ein RSA - Systems beinhaltet die Einrichtung große Primzahlen Auswahl $p$ und $q$ , Rechen $n = pq$ und $k = φ (n)$ , und die Suche nach zwei Zahlen $e$ und $d$ , so daß $ed \equiv 1 (mod k)$ . Die Zahlen $n$ und $e$ (der "Verschlüsselungsschlüssel") werden der Öffentlichkeit zugänglich gemacht und $d$ (der "Entschlüsselungsschlüssel") wird geheim gehalten.

Eine Nachricht, dargestellt durch eine ganze Zahl $m$ , wobei $0 < m < n ist$ , wird durch Berechnen von $S = m e (mod n)$ verschlüsselt .

Es wird entschlüsselt, indem man $t = S d (mod n)$ berechnet . Der Satz von Euler kann verwendet werden, um zu zeigen, dass wenn $0 < t < n ist$ , dann $t = m ist$ .

Die Sicherheit eines RSA - System würde , wenn die Zahl beeinträchtigt wird $n$ berücksichtigt werden könnte oder wenn $φ (n)$ könnte ohne Factoring berechnet werden $n$ .

Ungelöste Probleme

Lehmers Vermutung

Wenn $p$ eine Primzahl ist, dann gilt $φ (p) = p - 1$ . 1932 fragte DH Lehmer , ob es zusammengesetzte Zahlen $n gibt,$ so dass $φ (n)$ $n - 1$ teilt . Keine sind bekannt.

1933 bewies er, dass wenn ein solches $n$ existiert, es ungerade, quadratfrei und durch mindestens sieben Primzahlen teilbar sein muss (dh $ω (n) \geq 7$ ). 1980 bewiesen Cohen und Hagis, dass $n > 10 20$ und $ω (n) \geq 14 ist$ . Darüber hinaus zeigte Hagis, dass wenn 3 $n$ teilt, dann $n > 10 1937042$ und $ω (n) 298848$ .

Carmichaels Vermutung

Darin heißt es, dass es keine Zahl $n$ mit der Eigenschaft , dass für alle anderen Zahlen $m$ , $m \neq n$ , $φ (m) \neq φ (n)$ . Siehe den Satz von Ford oben.

Wie im Hauptartikel erwähnt, muss es, wenn es ein einziges Gegenbeispiel zu dieser Vermutung gibt, unendlich viele Gegenbeispiele geben, und das kleinste hat mindestens zehn Milliarden Stellen zur Basis 10.

Siehe auch

Anmerkungen

Verweise

Die Disquisitiones Arithmeticae wurde aus dem Lateinischen ins Englische und Deutsche übersetzt. Die deutsche Ausgabe enthält alle Arbeiten von Gauß zur Zahlentheorie: alle Beweise der quadratischen Reziprozität, die Vorzeichenbestimmung der Gauß-Summe, die Untersuchungen zur biquadratischen Reziprozität und unveröffentlichte Notizen.

Verweise auf die Disquisitionen haben die Form Gauss, DA, Art. nnn .

Abramowitz, M. ; Stegun, IA (1964), Handbook of Mathematical Functions , New York: Dover Publications , ISBN 0-486-61272-4. Siehe Abschnitt 24.3.2.
Bach, Eric ; Shallit, Jeffrey (1996), Algorithmic Number Theory (Band I: Efficient Algorithms) , MIT Press Series in the Foundations of Computing, Cambridge, MA: The MIT Press , ISBN 0-262-02405-5, Zbl 0873.11070
Dickson, Leonard Eugene, "History Of The Theory Of Numbers", Band 1, Kapitel 5 "Euler's Function, Generalizations; Farey Series", Chelsea Publishing 1952
Ford, Kevin (1999), "Die Zahl der Lösungen von φ( x ) = m ", Annals of Mathematics , 150 (1): 283–311, doi : 10.2307/121103 , ISSN 0003-486X , JSTOR 121103 , MR 1715326 , Zbl 0978.11053.
Gauß, Carl Friedrich ; Clarke, Arthur A. (Übersetzer ins Englische) (1986), Disquisitiones Arithmeticae (zweite, korrigierte Auflage) , New York: Springer , ISBN 0-387-96254-9
Gauß, Carl Friedrich ; Maser, H. (Übersetzer ins Deutsche) (1965), Untersuchungen über höhere Arithmetik (Disquisitiones Arithmeticae & other papers on number Theory) (Zweite Auflage) , New York: Chelsea, ISBN 0-8284-0191-8
Graham, Ronald ; Knuth, Donald ; Patashnik, Oren (1994), Konkrete Mathematik : eine Grundlage für die Informatik (2. Aufl.), Reading, MA: Addison-Wesley, ISBN 0-201-55802-5, Zbl 0836.00001
Guy, Richard K. (2004), Unsolved Problems in Number Theory , Problem Books in Mathematics (3. Aufl.), New York, NY: Springer-Verlag , ISBN 0-387-20860-7, Zbl 1058.11001
Hardy, GH ; Wright, EM (1979), An Introduction to the Theory of Numbers (Fünfte Aufl.), Oxford: Oxford University Press , ISBN 978-0-19-853171-5
Long, Calvin T. (1972), Elementary Introduction to Number Theory (2. Aufl.), Lexington: DC Heath and Company , LCCN 77-171950
Pettofrezzo, Anthony J.; Byrkit, Donald R. (1970), Elemente der Zahlentheorie , Englewood Cliffs: Prentice Hall , LCCN 77-81766
Ribenboim, Paulo (1996), The New Book of Prime Number Records (3. Aufl.), New York: Springer , ISBN 0-387-94457-5, Zbl 0856.11001
Sandifer, Charles (2007), Die frühe Mathematik von Leonhard Euler , MAA, ISBN 0-88385-559-3
Sandor, József; Mitrinović, Dragoslav S.; Crstici, Borislav, Hrsg. (2006), Handbuch der Zahlentheorie I , Dordrecht: Springer-Verlag , S. 9–36, ISBN 1-4020-4215-9, Zbl 1151.11300
Sandor, Jozsef; Crstici, Borislav (2004). Handbuch der Zahlentheorie II . Dordrecht: Kluwer Akademiker. S. 179 –327. ISBN 1-4020-2546-7. Zbl 1079.11001 .
Schramm, Wolfgang (2008), "Die Fourier-Transformation von Funktionen des größten gemeinsamen Teilers" , Electronic Journal of Combinatorial Number Theory , A50 (8(1)).

Externe Links

"Totient-Funktion" , Encyclopedia of Mathematics , EMS Press , 2001 [1994]
Eulersche Phi-Funktion und der chinesische Restsatz — Beweis, dass $φ (n)$ multiplikativ ist
Eulers Totient-Funktionsrechner in JavaScript – bis zu 20 Stellen
Dineva-, Rosica-, Euler-Totient-, Möbius- und Divisor-Funktionen
Plytage, Loomis, Polhill fassen die Euler-Phi-Funktion zusammen

Languages

In other projects