Fiktive Kraft - Fictitious force

Teil einer Serie über
Klassische Mechanik
${\displaystyle {\textbf {F}}={\frac {d}{dt}}(m{\textbf {v}})}$ Zweites Bewegungsgesetz
Geschichte Zeitleiste Lehrbücher
Geäst
Grundlagen
Formulierungen
Kernthemen
Drehung
Wissenschaftler
Physikportal  Kategorie
v T e

Eine fiktive Kraft (auch Pseudokraft , d'Alembert-Kraft oder Trägheitskraft genannt ) ist eine Kraft , die auf eine Masse zu wirken scheint, deren Bewegung unter Verwendung eines nicht-Trägheitsbezugssystems beschrieben wird , z. B. eines beschleunigenden oder rotierenden Bezugssystems . Ein Beispiel ist ein nach vorne beschleunigender Pkw – die Fahrgäste nehmen wahr, dass sie nach hinten von einer Kraft beaufschlagt werden, die sie in ihre Sitze zurückdrängt. Ein Beispiel in einem rotierenden Bezugssystem ist die Kraft, die Objekte nach außen zum Rand einer Zentrifuge zu drücken scheint. Diese scheinbaren Kräfte sind Beispiele für fiktive Kräfte.

Die fiktive Kraft F ist auf die Trägheit eines Objekts zurückzuführen, wenn sich das Referenzsystem nicht trägheitshalber bewegt und somit relativ zum freien Objekt zu beschleunigen beginnt. Die fiktive Kraft entsteht also nicht aus einer physikalischen Wechselwirkung zwischen zwei Objekten, wie Elektromagnetismus oder Kontaktkräften , sondern aus der Beschleunigung a des nichtinertialen Bezugssystems selbst, das aus der Sicht des Bezugssystems nun als Beschleunigung erscheint des Objekts statt, was eine "Kraft" erfordert, um dies zu erreichen. Wie von Iro gesagt:

Eine solche zusätzliche Kraft aufgrund einer ungleichmäßigen Relativbewegung zweier Referenzsysteme wird als Pseudokraft bezeichnet .

—  H. Iro in A Modern Approach to Classical Mechanics p. 180

Unter der Annahme des zweiten Newtonschen Gesetzes in der Form F  =  m a sind fiktive Kräfte immer proportional zur Masse m .

Die fiktive Kraft auf ein Objekt entsteht als imaginärer Einfluss, wenn der zur Beschreibung der Bewegung des Objekts verwendete Bezugssystem im Vergleich zu einem nicht beschleunigenden Bezugssystem beschleunigt. Die fiktive Kraft „erklärt“ mit Hilfe der Newtonschen Mechanik, warum ein Objekt nicht den Newtonschen Gesetzen folgt und wie schwerelos „frei schwebt“. So wie ein Rahmen beliebig beschleunigen kann, können auch fiktive Kräfte beliebig sein (aber nur in direkter Reaktion auf die Beschleunigung des Rahmens). Es werden jedoch vier fiktive Kräfte für Rahmen definiert, die auf übliche Weise beschleunigt werden: eine, die durch eine beliebige relative Beschleunigung des Ursprungs in einer geraden Linie (geradlinige Beschleunigung ) verursacht wird; zwei mit Rotation: Zentrifugalkraft und Corioliskraft ; und eine vierte, die Euler-Kraft genannt wird , die durch eine variable Rotationsrate verursacht wird, sollte dies auftreten.

Die Gravitationskraft wäre auch eine fiktive Kraft, die auf einem Feldmodell basiert, in dem Teilchen die Raumzeit aufgrund ihrer Masse verzerren , wie etwa der Allgemeinen Relativitätstheorie .

Im Trägheitsbezugssystem (oberer Teil des Bildes) bewegt sich die schwarze Kugel geradlinig. Der im rotierenden/nicht-inertialen Bezugssystem (unterer Teil des Bildes) stehende Beobachter (brauner Punkt) sieht das Objekt jedoch aufgrund der in diesem Bezugssystem vorhandenen Coriolis- oder Fliehkräfte als einer gekrümmten Bahn folgend.

Hintergrund

Die Rolle fiktiver Kräfte in der Newtonschen Mechanik wird von Tonnelat beschrieben :

Für Newton weist das Auftreten von Beschleunigung immer auf die Existenz einer absoluten Bewegung hin – eine absolute Bewegung der Materie, wenn es um reale Kräfte geht; absolute Bewegung des Bezugssystems, wenn es sich um sogenannte fiktive Kräfte wie Trägheitskräfte oder die von Coriolis handelt.

—  Marie-Antoinette Tonnelat in The Principles of Electromagnetic Theory and Relativity , p. 113

Fiktive Kräfte treten in der klassischen Mechanik und der speziellen Relativitätstheorie in allen Nicht-Inertialsystemen auf. Inertialrahmen werden gegenüber Nicht-Inertialrahmen bevorzugt , da sie keine Physik haben, deren Ursachen außerhalb des Systems liegen, während dies bei Nicht-Inertialrahmen der Fall ist. Fiktive Kräfte oder Physik, deren Ursache außerhalb des Systems liegt, sind in der Allgemeinen Relativitätstheorie nicht mehr notwendig , da diese Physik mit der Geodäten der Raumzeit erklärt wird .

Auf der Erde

Die Erdoberfläche ist ein rotierendes Referenzsystem . Um klassische mechanische Probleme exakt in einem erdgebundenen Bezugssystem zu lösen , müssen drei fiktive Kräfte eingeführt werden: die Corioliskraft , die Fliehkraft (unten beschrieben) und die Eulerkraft . Die Euler-Kraft wird normalerweise ignoriert, da die Schwankungen der Winkelgeschwindigkeit der rotierenden Erdoberfläche normalerweise unbedeutend sind. Die beiden anderen fiktiven Kräfte sind im Vergleich zu den meisten typischen Kräften im Alltag schwach, können aber unter sorgfältigen Bedingungen nachgewiesen werden. Zum Beispiel Léon Foucault nutzte seine Foucaultsches Pendel , dass eine zeigen Corioliskraft ergibt sich aus der Erdrotation. Wenn sich die Erde zwanzigmal schneller drehen würde (jeder Tag nur ~72 Minuten lang), könnten die Menschen leicht den Eindruck bekommen, dass solche fiktiven Kräfte an ihnen ziehen, wie an einem sich drehenden Karussell; Menschen in gemäßigten und tropischen Breiten müssten sich tatsächlich festhalten, um nicht durch die Zentrifugalkraft in die Umlaufbahn geschleudert zu werden.

Erkennung von nichtinertialen Referenzrahmen

Beobachter in einem geschlossenen Kasten, der sich mit konstanter Geschwindigkeit bewegt, können ihre eigene Bewegung nicht erkennen; Beobachter innerhalb eines sich beschleunigenden Bezugssystems können jedoch anhand der auftretenden fiktiven Kräfte erkennen, dass sie sich in einem nicht inertialen Bezugssystem befinden. Für die geradlinige Beschleunigung stellt Vladimir Arnold beispielsweise den folgenden Satz vor:

In einem Koordinatensystem K, das sich relativ zu einem Inertialsystem k translatorisch bewegt , erfolgt die Bewegung eines mechanischen Systems so, als ob das Koordinatensystem träge wäre, aber auf jeden Massenpunkt m wirkt eine zusätzliche "Trägheitskraft": F  = − m a , wobei a die Beschleunigung des Systems K ist .

Auch andere Beschleunigungen führen zu fiktiven Kräften, wie im Folgenden mathematisch beschrieben . Die physikalische Erklärung von Bewegungen in einem Inertialsystem ist die einfachste mögliche und erfordert keine fiktiven Kräfte: Die fiktiven Kräfte sind null, was ein Mittel zur Unterscheidung von Inertialsystemen bietet.

Ein Beispiel für die Erkennung eines nicht inertialen, rotierenden Referenzsystems ist die Präzession eines Foucaultschen Pendels . Im Nicht-Trägheitssystem der Erde ist die fiktive Corioliskraft notwendig, um Beobachtungen zu erklären. In einem Inertialsystem außerhalb der Erde ist keine solche fiktive Kraft erforderlich.

Beispiele

Beschleunigung in gerader Linie

Abbildung 1: Oberes Panel : Beschleunigungswagen der Masse M mit Passagier der Masse m . Die Kraft von der Achse ist ( m + M ) a . Im Trägheitsrahmen ist dies die einzige Kraft auf Auto und Beifahrer.
Mittelteil : eine Explosionsansicht im Trägheitsrahmen. Der Passagier ist der Beschleunigungskraft m a ausgesetzt . Der Sitz (von einer vernachlässigbaren Masse angenommen) wird zwischen der Reaktionskraft – m a und der von der Kabine ausgeübten Kraft m a zusammengedrückt . Das Auto unterliegt der Nettobeschleunigungskraft M a , die die Differenz zwischen der aufgebrachten Kraft ( m + M ) a von der Achse und der Reaktion vom Sitz – m a ist .
Unteres Panel : eine Explosionsansicht im Nicht-Trägheitsrahmen. Im Nicht-Trägheitsrahmen, in dem das Auto nicht beschleunigt, wird die Kraft von der Achse durch eine fiktive Rückwärtskraft –( m + M ) a , einen auf das Auto aufgebrachten Anteil – M a und – m a auf den Fahrgast ausgeglichen . Auf das Auto wirken die fiktive Kraft − M a und die Kraft ( m + M ) a von der Achse. Die Summe dieser Kräfte m a wird auf den Sitz ausgeübt, der eine Reaktion − m a auf das Auto ausübt , sodass auf das Auto keine Nettokraft ausgeübt wird. Der Sitz (angenommen masselos) überträgt die Kraft m a auf den Passagier, der auch der fiktiven Kraft − m a ausgesetzt ist, sodass auf den Passagier keine Nettokraft entsteht. Der Passagier übt eine Reaktionskraft − m a auf den Sitz aus, der dadurch gestaucht wird. Bei allen Rahmen ist die Kompression des Sitzes gleich und die von der Achse gelieferte Kraft ist gleich.

Abbildung 1 (oben) zeigt ein beschleunigendes Auto. Wenn ein Auto beschleunigt , fühlt sich ein Beifahrer wie in den Sitz zurückgeschoben. In einem an der Straße befestigten Trägheitsbezugssystem gibt es keine physische Kraft, die den Fahrer nach hinten bewegt. Jedoch gibt es in dem nicht-trägheitsbezogenen Referenzrahmen des Fahrers, der an dem beschleunigenden Auto angebracht ist, eine rückwärts gerichtete fiktive Kraft. Wir nennen zwei mögliche Gründe für die Kraft, um ihre (die Kraft) Existenz zu klären:

• Abbildung 1 (Mitteltafel). Für einen Beobachter, der auf einem Trägheitsbezugssystem (wie dem Boden) ruht , scheint das Auto zu beschleunigen. Damit der Passagier im Auto bleiben kann, muss eine Kraft auf den Passagier ausgeübt werden. Diese Kraft wird vom Sitz ausgeübt, der sich mit dem Auto nach vorne bewegt und gegen den Passagier gedrückt wird, bis er die volle Kraft überträgt, um den Passagier mit dem Auto in Bewegung zu halten. Dadurch sind die vom Sitz ausgeübten Kräfte unausgeglichen, sodass der Passagier in diesem Rahmen beschleunigt.
• Abbildung 1 (Unterseite). Aus der Sicht des Innenraums des Autos, einem Beschleunigungsbezugssystem, gibt es eine fiktive Kraft, die den Passagier nach hinten drückt, mit einer Größe gleich der Masse des Passagiers mal der Beschleunigung des Autos. Diese Kraft drückt den Passagier zurück in den Sitz, bis sich der Sitz zusammendrückt und eine gleiche und entgegengesetzte Kraft erzeugt. Danach steht der Passagier in diesem Rahmen still, da die fiktive Kraft und die reale Kraft des Sitzes ausgeglichen sind.

Es wird entdeckt, dass der Beschleunigungsrahmen nicht träge ist, da im Beschleunigungsrahmen alles einer Null-Nettokraft unterworfen zu sein scheint und sich nichts bewegt. Nichtsdestotrotz wird eine Kompression des Sitzes beobachtet und wird im Beschleunigungsrahmen (und in einem Trägheitsrahmen) durch die Kraft der Beschleunigung auf den Sitz vom Auto auf einer Seite und der Gegenkraft der Reaktion auf die Beschleunigung durch den Passagier auf der Seite erklärt Sonstiges. Die Identifizierung des Beschleunigungsrahmens als Nicht-Trägheitsrahmen kann nicht allein auf der Kompression des Sitzes beruhen, die alle Beobachter erklären können; sie basiert vielmehr auf der Einfachheit der physikalischen Erklärung für diese Komprimierung.

Die Erklärung der Sitzkompression im Beschleunigungsrahmen erfordert nicht nur den Schub von der Achse des Autos, sondern zusätzliche (fiktive) Kräfte. In einem Trägheitsrahmen ist nur der Schub von der Achse notwendig. Daher hat der Trägheitsrahmen eine einfachere physikalische Erklärung (nicht unbedingt eine einfachere mathematische Formulierung), die anzeigt, dass der Beschleunigungsrahmen ein Nicht-Trägheitsbezugssystem ist. Mit anderen Worten, im Inertialsystem sind die fiktiven Kräfte null. Siehe Inertialsystem .

Dieses Beispiel veranschaulicht, wie fiktive Kräfte beim Wechsel von einem Trägheits- zu einem Nicht-Trägheitsbezugssystem entstehen. Berechnungen physikalischer Größen (Kompression des Sitzes, erforderliche Kraft von der Achse) in einem beliebigen Rahmen geben die gleichen Antworten, aber in einigen Fällen sind Berechnungen in einem Nicht-Trägheitsrahmen einfacher durchzuführen. (In diesem einfachen Beispiel sind die Berechnungen für die beiden beschriebenen Frames gleich komplex.)

Animation: von Block zu Block fahren
Karten- und Autorahmenperspektiven von physischen (rot) und fiktiven (blau) Kräften für ein Auto, das von einem Stoppschild zum nächsten fährt In dieser Abbildung beschleunigt das Auto nach einem Stoppschild bis zur Mitte des Blocks, woraufhin der Fahrer sofort vom Gas geht und auf die Bremse tritt, um den nächsten Halt einzulegen.

Kreisbewegung

Ein ähnlicher Effekt tritt bei kreisförmiger Bewegung auf , kreisförmig vom Standpunkt eines an der Straße angebrachten Trägheitsbezugssystems. Von einem nicht inertialen Bezugssystem aus gesehen, das am Auto angebracht ist, erscheint die fiktive Kraft, die als Zentrifugalkraft bezeichnet wird . Bewegt sich das Auto mit konstanter Geschwindigkeit auf einem kreisförmigen Straßenabschnitt, fühlen sich die Insassen durch diese Fliehkraft nach außen, weg von der Kurvenmitte, gedrängt. Auch hier kann die Situation aus Trägheits- oder Nicht-Trägheitsrahmen betrachtet werden:

• Aus der Sicht eines in Bezug auf die Straße feststehenden Trägheitsbezugssystems beschleunigt das Auto in Richtung des Kreismittelpunkts. Diese Beschleunigung ist notwendig, da sich trotz konstanter Geschwindigkeit die Richtung der Geschwindigkeit ändert. Diese Beschleunigung nach innen wird als Zentripetalbeschleunigung bezeichnet und erfordert eine Zentripetalkraft , um die Kreisbewegung aufrechtzuerhalten. Diese Kraft wird vom Boden auf die Räder ausgeübt, in diesem Fall von der Reibung zwischen den Rädern und der Straße. Das Auto beschleunigt aufgrund der unausgeglichenen Kraft, die dazu führt, dass es sich im Kreis bewegt. (Siehe auch Steilkurve .)
• Aus der Sicht eines rotierenden Rahmens, der sich mit dem Auto bewegt, gibt es eine fiktive Zentrifugalkraft, die dazu neigt, das Auto zur Außenseite der Straße zu drücken (und die Insassen zur Außenseite des Autos zu drücken). Die Zentrifugalkraft gleicht die Reibung zwischen Rädern und Straße aus, wodurch das Auto in diesem Nicht-Trägheitsrahmen steht.

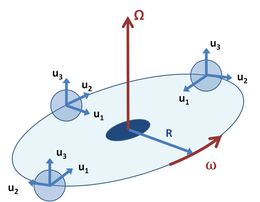
Ein klassisches Beispiel für eine fiktive Kraft in Kreisbewegung ist das Experiment mit rotierenden Kugeln, die mit einer Schnur verbunden sind und sich um ihren Massenschwerpunkt drehen. In diesem Fall kann, wie beim Beispiel mit linear beschleunigendem Auto, die Identifizierung eines rotierenden, nicht inertialen Bezugssystems auf dem Verschwinden fiktiver Kräfte basieren. In einem Inertialsystem sind keine fiktiven Kräfte erforderlich, um die Spannung in der die Kugeln verbindenden Schnur zu erklären. In einem rotierenden Rahmen müssen Coriolis- und Zentrifugalkräfte eingeleitet werden, um die beobachtete Spannung vorherzusagen.

Im rotierenden Bezugssystem, das auf der Erdoberfläche wahrgenommen wird, reduziert die Zentrifugalkraft die scheinbare Schwerkraft je nach Breitengrad um etwa einen Tausendstel. Diese Reduktion ist an den Polen null, am Äquator maximal .

Animation: Objekt aus einem Karussell freigesetzt

Karten- und Drehrahmenperspektiven von physikalischen (rot) und fiktiven (blau) Kräften für ein aus einem Karussell freigesetztes Objekt Aus der Perspektive des Kartenrahmens kann die Geschwindigkeit beim Verlust der Zentripetalbeschleunigung gefährlich sein. Aus Sicht des Drehrahmens könnte die Gefahr stattdessen in der geometrischen Beschleunigung liegen, die diese fiktive Kraft verursacht. Hinweis: Bei einigen Browsern wird durch Drücken von [Esc] die Bewegung für eine detailliertere Analyse eingefroren. Möglicherweise muss die Seite jedoch neu geladen werden, um neu zu starten.

Die fiktive Corioliskraft , die in Rotationssystemen beobachtet wird, ist normalerweise nur in sehr großräumigen Bewegungen sichtbar, wie der Projektilbewegung von Langstreckengeschützen oder der Zirkulation der Erdatmosphäre (siehe Rossby-Nummer ). Unter Vernachlässigung des Luftwiderstands fällt ein Objekt, das von einem 50 Meter hohen Turm am Äquator abgeworfen wird, 7,7 Millimeter östlich von der Stelle darunter, an der es aufgrund der Corioliskraft abgeworfen wird.

Bei weit entfernten Objekten und rotierendem Bezugssystem ist die resultierende Kraft aus Zentrifugal- und Corioliskräften zu berücksichtigen. Stellen Sie sich einen entfernten Stern vor, der von einem rotierenden Raumfahrzeug aus beobachtet wird. In dem mit dem Raumfahrzeug mitrotierenden Bezugssystem scheint sich der entfernte Stern entlang einer kreisförmigen Flugbahn um das Raumfahrzeug herum zu bewegen. Die scheinbare Bewegung des Sterns ist eine scheinbare Zentripetalbeschleunigung. Die Fliehkraft hat genau wie im obigen Beispiel des kreisenden Autos die gleiche Größe wie die fiktive Fliehkraft, ist jedoch in die entgegengesetzte, zentrifugale Richtung gerichtet. In diesem Fall ist die Corioliskraft doppelt so groß wie die Zentrifugalkraft und zeigt in zentripetaler Richtung. Die Vektorsumme aus Zentrifugalkraft und Corioliskraft ist die fiktive Gesamtkraft, die in diesem Fall in Zentripetalrichtung zeigt.

Fiktive Kräfte und Arbeit

Fiktive Kräfte können als Arbeit betrachtet werden , sofern sie ein Objekt auf einer Bahn bewegen , die seine Energie von potentiell zu kinetisch ändert . Stellen Sie sich zum Beispiel eine Person in einem rotierenden Stuhl vor, die ein Gewicht in der ausgestreckten Hand hält. Ziehen sie die Hand aus der Perspektive des rotierenden Bezugssystems nach innen zu ihrem Körper, haben sie Arbeit gegen die Fliehkraft geleistet. Wenn das Gewicht losgelassen wird, fliegt es relativ zum rotierenden Bezugssystem spontan nach außen, da die Fliehkraft auf das Objekt wirkt und seine potentielle Energie in Bewegungsenergie umwandelt. Aus Trägheitssicht fliegt das Objekt natürlich von ihnen weg, weil es sich plötzlich geradlinig bewegen darf. Dies veranschaulicht, dass die geleistete Arbeit, wie das gesamte Potenzial und die kinetische Energie eines Objekts, in einem Nicht-Inertialsystem anders sein kann als in einem Inertialsystem.

Schwerkraft als fiktive Kraft

Der Begriff der "fiktiven Kraft" taucht in Einsteins allgemeiner Relativitätstheorie auf. Alle fiktiven Kräfte sind proportional zur Masse des Objekts, auf das sie wirken, was auch für die Schwerkraft gilt . Dies führte Albert Einstein zu der Frage, ob die Schwerkraft auch eine fiktive Kraft sei. Er bemerkte, dass ein frei fallender Beobachter in einer geschlossenen Kiste die Schwerkraft nicht wahrnehmen könnte; daher sind frei fallende Referenzsysteme äquivalent zu einem Trägheitsreferenzsystem (das Äquivalenzprinzip ). Anknüpfend an diese Erkenntnis konnte Einstein eine Theorie mit der Schwerkraft als fiktiver Kraft formulieren und die scheinbare Schwerkraftbeschleunigung auf die Krümmung der Raumzeit zurückführen . Diese Idee liegt Einsteins allgemeiner Relativitätstheorie zugrunde . Siehe Eötvös-Experiment .

Animation: Ball, der von einer Klippe rollt

Regen und Muschel rahmen Perspektiven von physischen (rot) und fiktiven (blau) Kräften für ein Objekt ein, das von einer Klippe rollt. Hinweis: Die Regenrahmen-Perspektive hier ähnelt eher der eines Trampolinspringers, als die eines Regentropfens, dessen Flugbahn gerade dann ausläuft, wenn der Ball die Kante der Klippe erreicht. Die Schalenrahmen-Perspektive mag Planetenbewohnern bekannt sein, die sich minütlich auf nach oben gerichtete physikalische Kräfte aus ihrer Umgebung verlassen, um sie vor der geometrischen Beschleunigung aufgrund der gekrümmten Raumzeit zu schützen.

Mathematische Herleitung fiktiver Kräfte

Abbildung 2: Ein Objekt, das sich bei x _A im Inertialsystem A befindet, befindet sich am Ort x _B im Beschleunigungssystem B . Der Ursprung von Frame B liegt bei X _AB in Frame A . Die Ausrichtung des Rahmens B wird durch die Einheitsvektoren entlang der Koordinatenrichtungen, bestimmt u _j mit j = 1, 2, 3. Mit Hilfe dieser Achsen werden die Koordinaten des Objekts gemäß Rahmen B sind x _B = ( x ₁ , x ₂ , x ₃ ).

Allgemeine Herleitung

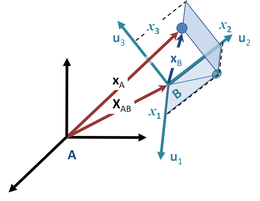
Viele Probleme erfordern die Verwendung nichtinertialer Referenzsysteme, zum Beispiel solche, die Satelliten und Teilchenbeschleuniger beinhalten. Figur 2 zeigt ein Teilchen mit Masse m und Positionsvektor x _A ( t ) in einem bestimmten Inertialsystem A. Betrachten wir ein nicht-Inertialsystem B , dessen Ursprung in Bezug auf die Trägheits eins wird gegeben durch X _AB ( t ). Die Position des Partikels im Frame B sei x _B ( t ). Wie groß ist die Kraft auf das Teilchen, ausgedrückt im Koordinatensystem des Systems B?

Um diese Frage zu beantworten, sei die Koordinatenachse in B durch Einheitsvektoren u _j mit j beliebige { 1, 2, 3 } für die drei Koordinatenachsen dargestellt. Dann

${\displaystyle \mathbf {x} _{\mathrm {B} }=\sum _{j=1}^{3}x_{j}\mathbf {u} _{j}\ .}$

Die Interpretation dieser Gleichung ist, dass x _B die Vektorverschiebung des Partikels ist, ausgedrückt durch die Koordinaten im Rahmen B zum Zeitpunkt t . Ab Frame A befindet sich das Partikel an:

${\displaystyle \mathbf {x} _{\mathrm {A} }=\mathbf {X} _{\mathrm {AB} }+\sum _{j=1}^{3}x_{j}\mathbf { u} _{j}\ .}$

Abgesehen davon können die Einheitsvektoren {  u _j  } ihre Größe nicht ändern, sodass Ableitungen dieser Vektoren nur die Drehung des Koordinatensystems B ausdrücken. Andererseits lokalisiert der Vektor X _AB einfach den Ursprung von Frame B relativ zu Frame A, und kann also die Drehung von Frame B nicht einschließen.

Bei einer zeitlichen Ableitung beträgt die Geschwindigkeit des Teilchens:

${\displaystyle {\frac {d\mathbf {x} _{\mathrm {A}}}{dt}}={\frac {d\mathbf {X} _{\mathrm {AB} }}{dt}} +\sum _{j=1}^{3}{\frac {dx_{j}}{dt}}\mathbf {u} _{j}+\sum _{j=1}^{3}x_{ j}{\frac{d\mathbf{u} _{j}}{dt}}\ .}$

Die Summation des zweiten Termes ist die Geschwindigkeit des Teilchens, sagen wir v _B , gemessen im System B. Das heißt:

${\ Display {\ frac {d \ mathbf {x} _ {\ mathrm {A}}} {dt}} = \ mathbf {v} _ {\ mathrm {AB}} + \ mathbf {v} _ {\ mathrm {B} }+\sum_{j=1}^{3}x_{j}{\frac {d\mathbf{u}_{j}}{dt}}.}$

Die Interpretation dieser Gleichung ist, dass die Geschwindigkeit des Teilchens, die von Beobachtern in Bezugssystem A gesehen wird, aus dem besteht, was Beobachter in Bezugssystem B die Geschwindigkeit nennen, nämlich v _B , plus zwei zusätzliche Terme, die sich auf die Änderungsrate der Koordinatenachsen von Bezugssystem B beziehen . Eine davon ist einfach die Geschwindigkeit des bewegten Ursprungs v _AB . Der andere ist ein Beitrag zur Geschwindigkeit aufgrund der Tatsache, dass verschiedene Orte in dem Nicht-Inertialsystem aufgrund der Rotation des Rahmens unterschiedliche scheinbare Geschwindigkeiten haben; ein Punkt, der von einem rotierenden Rahmen aus gesehen wird, hat eine Rotationsgeschwindigkeitskomponente, die umso größer ist, je weiter der Punkt vom Ursprung entfernt ist.

Um die Beschleunigung zu finden, liefert eine weitere Zeitdifferenzierung:

${\displaystyle {\frac {d^{2}\mathbf {x} _{\mathrm {A}}}{dt^{2}}}=\mathbf {a} _{\mathrm {AB} }+{ \frac{d\mathbf{v}_{\textrm{B}}}{dt}}+\sum_{j=1}^{3}{\frac{dx_{j}}{dt}}{\ frac {d\mathbf {u}_{j}}{dt}}+\sum_{j=1}^{3}x_{j}{\frac {d^{2}\mathbf {u} _{ j}}{dt^{2}}}.}$

Unter Verwendung der gleichen Formel, die bereits für die Zeitableitung von x _{B verwendet wurde} , lautet die Geschwindigkeitsableitung rechts:

${\displaystyle {\frac {d\mathbf {v} _{\mathrm {B}}}{dt}}=\sum _{j=1}^{3}{\frac {dv_{j}}{dt }}\mathbf {u}_{j}+\sum_{j=1}^{3}v_{j}{\frac {d\mathbf {u}_{j}}{dt}}=\mathbf {a}_{\mathrm{B}}+\sum_{j=1}^{3}v_{j}{\frac {d\mathbf{u}_{j}}{dt}}.}$

Folglich,

${\displaystyle {\frac {d^{2}\mathbf {x} _{\mathrm {A}}}{dt^{2}}}=\mathbf {a} _{\mathrm {AB} }+\ mathbf {a} _{\mathrm {B} }+2\ \sum_{j=1}^{3}v_{j}{\frac {d\mathbf {u} _{j}}{dt}} +\sum_{j=1}^{3}x_{j}{\frac {d^{2}\mathbf {u} _{j}}{dt^{2}}}.}$

( 1 )

Die Interpretation dieser Gleichung ist wie folgt: Die Beschleunigung des Teilchens im System A besteht aus dem, was Beobachter im System B die Teilchenbeschleunigung a _{B nennen} , aber zusätzlich gibt es drei Beschleunigungsterme, die sich auf die Bewegung der Koordinatenachsen von System B beziehen : ein Term, der sich auf die Beschleunigung des Ursprungs von Frame B bezieht , nämlich a _AB , und zwei Terme, die sich auf die Rotation von Frame B beziehen. Folglich werden Beobachter in B sehen, dass die Teilchenbewegung eine "zusätzliche" Beschleunigung besitzt, die sie zuschreiben "Kräfte", die auf das Teilchen wirken, die Beobachter in A aber als "fiktive" Kräfte bezeichnen, die einfach entstehen, weil Beobachter in B die Nicht-Trägheitsnatur des Systems B nicht erkennen.

Der Faktor zwei in der Corioliskraft ergibt sich aus zwei gleichen Beiträgen: (i) der scheinbaren Änderung einer trägheitskonstanten Geschwindigkeit mit der Zeit, weil die Rotation die Richtung der Geschwindigkeit zu ändern scheint (a d v _B /d t- Term) und ( ii) eine scheinbare Änderung der Geschwindigkeit eines Objekts, wenn sich seine Position ändert, wodurch es näher an oder weiter von der Rotationsachse entfernt wird (die Änderung aufgrund einer Änderung von x _j ). ${\displaystyle \sum x_{j}\,d\mathbf {u} _{j}/dt}$

Um es kräftemäßig auszudrücken, werden die Beschleunigungen mit der Teilchenmasse multipliziert:

${\displaystyle \mathbf {F} _{\mathrm {A} }=\mathbf {F} _{\mathrm {B} }+m\mathbf {a} _{\mathrm {AB} }+2m\sum _ {j=1}^{3}v_{j}{\frac {d\mathbf {u}_{j}}{dt}}+m\sum_{j=1}^{3}x_{j} {\frac {d^{2}\mathbf {u} _{j}}{dt^{2}}}\ .}$

Die im System B beobachtete Kraft F _B = m a _B steht in Beziehung zur tatsächlichen Kraft auf das Teilchen F _A , um

${\displaystyle \mathbf {F} _{\mathrm {B} }=\mathbf {F} _{\mathrm {A} }+\mathbf {F} _{\mathrm {fiktiv}},}$

wo:

${\displaystyle \mathbf {F} _{\mathrm {fiktiv} }=-m\mathbf {a} _{\mathrm {AB} }-2m\sum _{j=1}^{3}v_{j} {\frac {d\mathbf {u} _{j}}{dt}}-m\sum _{j=1}^{3}x_{j}{\frac {d^{2}\mathbf {u } _{j}}{dt^{2}}}\ .}$

Somit können wir Probleme im System B lösen, indem wir annehmen, dass das zweite Newtonsche Gesetz gilt (in Bezug auf Größen in diesem System) und F _fiktiv als zusätzliche Kraft behandeln.

Nachfolgend finden Sie eine Reihe von Beispielen, die dieses Ergebnis für fiktive Kräfte anwenden. Weitere Beispiele finden Sie im Artikel zur Fliehkraft .

Rotierende Koordinatensysteme

Eine übliche Situation, in der nichtinertiale Referenzrahmen nützlich sind, ist, wenn sich der Referenzrahmen dreht. Da eine solche Drehbewegung aufgrund der bei jeder Drehbewegung vorhandenen Beschleunigung nicht träge ist, kann immer eine fiktive Kraft unter Verwendung eines Drehbezugssystems hervorgerufen werden. Trotz dieser Komplikation vereinfacht die Verwendung fiktiver Kräfte oft die Berechnungen.

Um Ausdrücke für die fiktiven Kräfte abzuleiten, werden Ableitungen für die scheinbare zeitliche Änderungsrate von Vektoren benötigt, die die zeitliche Variation der Koordinatenachsen berücksichtigen. Wenn die Drehung des Rahmens 'B' durch einen Vektor Ω dargestellt wird, der entlang der Drehachse mit der durch die Rechte-Hand-Regel gegebenen Orientierung und mit der durch gegebenen Größe zeigt

${\displaystyle |{\boldsymbol {\Omega}}|={\frac {d\theta}{dt}}=\omega (t),}$

dann ist die zeitliche Ableitung eines der drei Einheitsvektoren, die den Rahmen B beschreiben,

${\displaystyle {\frac {d\mathbf {u}_{j}(t)}{dt}}={\boldsymbol {\Omega}}\times \mathbf {u}_{j}(t),}$

und

${\displaystyle {\frac {d^{2}\mathbf {u} _{j}(t)}{dt^{2}}}={\frac {d{\boldsymbol {\Omega}}}{dt }}\times \mathbf {u} _{j}+{\boldsymbol {\Omega}}\times {\frac {d\mathbf {u} _{j}(t)}{dt}}={\frac {d{\boldsymbol {\Omega}}}{dt}}\times \mathbf {u}_{j}+{\boldsymbol {\Omega}}\times \left[{\boldsymbol {\Omega}}\times \mathbf{u}_{j}(t)\right],}$

wie anhand der Eigenschaften des Vektorkreuzprodukts verifiziert wird . Diese Ableitungsformeln werden nun auf die Beziehung zwischen der Beschleunigung in einem Inertialsystem und derjenigen in einem Koordinatensystem angewendet, das sich mit der zeitlich veränderlichen Winkelgeschwindigkeit ω( t ) dreht . Aus dem vorherigen Abschnitt, in dem sich der Index A auf das Trägheitssystem und B auf den rotierenden Rahmen bezieht, wobei a _AB = 0 gesetzt wird, um jegliche Translationsbeschleunigung zu entfernen und sich nur auf die Rotationseigenschaften zu konzentrieren (siehe Gl. 1 ):

${\displaystyle {\frac {d^{2}\mathbf {x} _{\mathrm {A}}}{dt^{2}}}=\mathbf {a} _{\mathrm {B} }+2 \sum _{j=1}^{3}v_{j}\ {\frac {d\mathbf {u} _{j}}{dt}}}+\sum _{j=1}^{3}x_ {j}{\frac {d^{2}\mathbf {u} _{j}}{dt^{2}}},}$

${\displaystyle \mathbf {a} _{\mathrm {A} }=\mathbf {a} _{\mathrm {B} }+\ 2\sum _{j=1}^{3}v_{j}{ \boldsymbol {\Omega}}\times \mathbf{u}_{j}(t)+\sum_{j=1}^{3}x_{j}{\frac {d{\boldsymbol {\Omega} }}{dt}}\times \mathbf{u}_{j}\ +\sum _{j=1}^{3}x_{j}{\boldsymbol {\Omega}}\times \left[{\ Fettsymbol {\Omega}}\times \mathbf{u}_{j}(t)\right]}$

${\displaystyle =\mathbf {a} _{\mathrm {B}}+2{\boldsymbol {\Omega}}\times \sum_{j=1}^{3}v_{j}\mathbf {u} _{j}(t)+{\frac {d{\boldsymbol {\Omega}}}{dt}}\times \sum_{j=1}^{3}x_{j}\mathbf {u}_ {j}+{\boldsymbol {\Omega}}\times \left[{\boldsymbol {\Omega}}\times \sum _{j=1}^{3}x_{j}\mathbf {u} _{ j}(t)\rechts].}$

Das Sammeln von Termen ergibt die sogenannte Beschleunigungstransformationsformel :

${\displaystyle \mathbf {a} _{\mathrm {A} }=\mathbf {a} _{\mathrm {B} }+2{\boldsymbol {\Omega}}\times \mathbf {v} _{\ mathrm {B}} + {\ frac {d {\ boldsymbol {\ Omega}}} {dt}} \ times \ mathbf {x} _ {\ mathrm {B}} + {\ boldsymbol {\ Omega}} \ times \left({\boldsymbol {\Omega}}\times \mathbf{x}_{\textrm{B}}\right)\ .}$

Die physikalische Beschleunigung a _A aufgrund dessen, was Beobachter im Inertialsystem A als reale äußere Kräfte auf das Objekt bezeichnen, ist daher nicht einfach die Beschleunigung a _B , die von Beobachtern im Rotationssystem B gesehen wird, sondern hat mehrere zusätzliche geometrische Beschleunigungsterme, die mit der Rotation von B. Wie im Rotationssystem zu sehen, ergibt sich die Beschleunigung a _B des Teilchens durch Umordnung der obigen Gleichung zu:

${\displaystyle \mathbf {a} _{\mathrm {B} }=\mathbf {a} _{\mathrm {A} }-2{\boldsymbol {\Omega}}\times \mathbf {v} _{\ Mathrm {B} }-{\boldsymbol {\Omega}}\times ({\boldsymbol {\Omega}}\times \mathbf {x} _{\mathrm {B}})-{\frac {d{\boldsymbol {\Omega}}}{dt}}\times \mathbf{x}_{\mathrm{B}}.}$

Die Nettokraft auf das Objekt ist laut Beobachtern im rotierenden Rahmen F _B = m a _B . Wenn ihre Beobachtungen bei Anwendung der Newtonschen Gesetze zu der richtigen Kraft auf das Objekt führen sollen, müssen sie berücksichtigen, dass die zusätzliche Kraft F _fikt vorhanden ist, so dass das Endergebnis F _B = F _A + F _{fikt ist} . Somit ist die fiktive Kraft, die von Beobachtern in B verwendet wird, um das korrekte Verhalten des Objekts aus den Newtonschen Gesetzen zu erhalten, gleich:

${\displaystyle \mathbf {F} _{\mathrm {fikt} }=-2m{\boldsymbol {\Omega}}\times \mathbf {v} _{\mathrm {B}}-m{\boldsymbol {\Omega }}\times ({\boldsymbol {\Omega}}\times \mathbf {x}_{\mathrm {B}})-m{\frac {d{\boldsymbol {\Omega}}}{dt}}\ mal \mathbf{x}_{\mathrm{B}}.}$

Hier ist der erste Term die Corioliskraft , der zweite Term die Zentrifugalkraft und der dritte Term die Eulerkraft .

Umlaufende Koordinatensysteme

Abbildung 3: Ein umlaufendes Koordinatensystem B mit fester Orientierung , gezeigt zu drei verschiedenen Zeiten. Die Einheitsvektoren u _j , j = 1, 2, 3 drehen sich nicht , sondern behalten eine feste Orientierung, während sich der Ursprung des Koordinatensystems B mit konstanter Winkelgeschwindigkeit ω um die feste Achse Ω bewegt . Die Achse Ω geht durch den Ursprung des Inertialsystems A , so dass der Ursprung von Frame B einen festen Abstand R vom Ursprung des Inertialsystems A hat .

Als verwandtes Beispiel sei angenommen, dass sich das bewegte Koordinatensystem B mit einer konstanten Winkelgeschwindigkeit ω in einem Kreis des Radius R um den festen Ursprung des Trägheitssystems A dreht , aber seine Koordinatenachsen in der Orientierung festhält, wie in Abbildung 3. Die Beschleunigung von ein beobachteter Körper ist nun (siehe Gl. 1 ):

${\displaystyle {\frac {d^{2}\mathbf {x} _{A}}{dt^{2}}}=\mathbf {a} _{AB}+\mathbf {a} _{B} +2\ \sum _{j=1}^{3}v_{j}\ {\frac {d\mathbf {u} _{j}}{dt}}}$ ${\displaystyle +\sum_{j=1}^{3}x_{j}\ {\frac {d^{2}\mathbf{u}_{j}}{dt^{2}}}\ . }$

${\displaystyle =\mathbf {a} _{AB}\ +\mathbf {a} _{B}\ ,}$

wobei die Summationen null sind, da die Einheitsvektoren keine Zeitabhängigkeit haben. Der Ursprung von System B liegt gemäß Frame A bei:

${\displaystyle \mathbf{X} _{AB}=R\left(\cos(\omega t),\\sin(\omega t)\right)\ ,}$

führt zu einer Geschwindigkeit des Ursprungs von Frame B als:

${\displaystyle \mathbf {v} _{AB}={\frac {d}{dt}}\mathbf {X} _{AB}=\mathbf {\Omega \times X} _{AB}\ ,}$

führt zu einer Beschleunigung des Ursprungs von B gegeben durch:

${\displaystyle \mathbf {a} _{AB}={\frac {d^{2}}{dt^{2}}}\mathbf {X} _{AB}}$ ${\displaystyle =\mathbf {\Omega\\times} \left(\mathbf {\Omega\times X} _{AB}\right)}$ ${\displaystyle =-\omega^{2}\mathbf{X}_{AB}\ .}$

Denn der erste Term, der ist

${\displaystyle \mathbf {\Omega\\times} \left(\mathbf {\Omega\times X} _{AB}\right)\ ,}$

hat die gleiche Form wie der normale Fliehkraftausdruck:

${\displaystyle {\boldsymbol {\Omega}}\times \left({\boldsymbol {\Omega}}\times \mathbf {x} _{B}\right)\ ,}$

es ist eine natürliche Erweiterung der Standardterminologie (obwohl es für diesen Fall keine Standardterminologie gibt), diesen Begriff als "Fliehkraft" zu bezeichnen. Welche Terminologie auch immer gewählt wird, die Beobachter in System B müssen eine fiktive Kraft einführen, diesmal aufgrund der Beschleunigung aus der Bahnbewegung ihres gesamten Koordinatensystems, also radial nach außen weg vom Rotationszentrum des Ursprungs ihres Koordinatensystems:

${\displaystyle\mathbf{F}_{\mathrm{fikt}}=m\omega^{2}\mathbf{X}_{AB}\ ,}$

und von der Größe:

${\displaystyle |\mathbf{F} _{\mathrm {fikt}}|=m\omega ^{2}R\ .}$

Beachten Sie, dass diese "Fliehkraft" Unterschiede zum Fall eines rotierenden Rahmens aufweist. Im rotierenden Rahmen hängt die Zentrifugalkraft vom Abstand des Objekts vom Ursprung des Rahmens B ab , während im Fall eines umlaufenden Rahmens die Zentrifugalkraft unabhängig vom Abstand des Objekts vom Ursprung des Rahmens B ist , aber hängt stattdessen vom Abstand des Ursprungs von Frame B von seinem Rotationszentrum ab, was zu derselben fiktiven Zentrifugalkraft für alle in Frame B beobachteten Objekte führt .

Orbitieren und Rotieren

Abbildung 4: Ein umlaufendes Koordinatensystem B ähnlich Abbildung 3, in dem sich jedoch die Einheitsvektoren u _j , j = 1, 2, 3 zur Drehachse drehen, während sich der Ursprung des Koordinatensystems B mit konstanter Winkelgeschwindigkeit ω um . bewegt die feste Achse Ω .

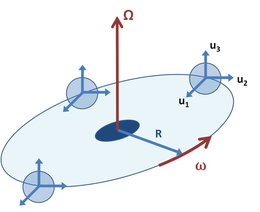
Als Kombination beispielsweise ein 4 zeigt Koordinatensystem B daß Orbits Inertialsystem A wie in Figur 3, aber die Koordinatenachsen in dem Rahmen B wiederum so Einheitsvektor u ₁ zeigt immer in Richtung des Zentrums der Rotation. Dieses Beispiel könnte auf ein Reagenzglas in einer Zentrifuge zutreffen, bei dem der Vektor u ₁ entlang der Achse des Röhrchens auf seine Öffnung an seiner Oberseite zeigt. Es ähnelt auch dem Erde-Mond-System, bei dem der Mond der Erde immer das gleiche Gesicht zeigt. In diesem Beispiel behält der Einheitsvektor u ₃ eine feste Orientierung, während die Vektoren u ₁ , u ₂ mit derselben Geschwindigkeit wie der Koordinatenursprung rotieren. Das ist,

${\displaystyle \mathbf {u} _{1}=(-\cos\omega t,\ -\sin\omega t)\ ;\ }$ ${\displaystyle \mathbf {u} _{2}=(\sin \omega t,\ -\cos \omega t)\ .}$

${\displaystyle {\frac {d}{dt}}\mathbf {u} _{1}=\mathbf {\Omega \times u_{1}} =\omega \mathbf {u} _{2}\ ;}$ ${\displaystyle \ {\frac {d}{dt}}\mathbf {u} _{2}=\mathbf {\Omega \times u_{2}} =-\omega \mathbf {u} _{1}\ \ .}$

Daher wird die Beschleunigung eines sich bewegenden Objekts ausgedrückt als (siehe Gl. 1 ):

${\displaystyle {\frac {d^{2}\mathbf {x} _{A}}{dt^{2}}}=\mathbf {a} _{AB}+\mathbf {a} _{B} +2\ \sum _{j=1}^{3}v_{j}\ {\frac {d\mathbf {u} _{j}}{dt}}}$ ${\displaystyle +\ \sum _{j=1}^{3}x_{j}\ {\frac {d^{2}\mathbf {u} _{j}}{dt^{2}}}\ }$

${\displaystyle =\mathbf {\Omega\\times} \left(\mathbf {\Omega\times X} _{AB}\right)+\mathbf {a} _{B}+2\\sum _{j =1}^{3}v_{j}\\mathbf{\Omega\times u_{j}}}$ ${\displaystyle \ +\ \sum _{j=1}^{3}x_{j}\ {\boldsymbol {\Omega}}\times \left({\boldsymbol {\Omega}}\times \mathbf {u } _{j}\rechts)\ }$

${\displaystyle =\mathbf {\Omega\\times} \left(\mathbf {\Omega\times X} _{AB}\right)+\mathbf {a} _{B}+2\ {\boldsymbol {\ Omega }}\times \mathbf{v}_{B}\}$ ${\displaystyle \ +\ {\boldsymbol {\Omega}}\times \left({\boldsymbol {\Omega}}\times \mathbf {x} _{B}\right)\ }$

${\displaystyle =\mathbf {\Omega\\times} \left(\mathbf {\Omega\times} (\mathbf{X}_{AB}+\mathbf{x}_{B})\right)+\ mathbf {a} _{B}+2\ {\boldsymbol {\Omega}}\times \mathbf {v} _{B}\ \ ,}$

wobei der Winkelbeschleunigungsterm bei konstanter Rotationsrate null ist. Denn der erste Term, der ist

${\displaystyle \mathbf {\Omega\\times} \left(\mathbf {\Omega\times} (\mathbf{X}_{AB}+\mathbf{x}_{B})\right)\ ,}$

hat die gleiche Form wie der normale Fliehkraftausdruck:

${\displaystyle {\boldsymbol {\Omega}}\times \left({\boldsymbol {\Omega}}\times \mathbf {x} _{B}\right)\ ,}$

es ist eine natürliche Erweiterung der Standardterminologie (obwohl es für diesen Fall keine Standardterminologie gibt), diesen Begriff als "Fliehkraft" zu bezeichnen. Wendet man diese Terminologie auf das Beispiel eines Röhrchens in einer Zentrifuge an, wenn das Röhrchen weit genug vom Rotationszentrum entfernt ist, | X _AB | = R ≫ | x _B |, alle Materie im Reagenzglas erfährt die gleiche Beschleunigung (die gleiche Zentrifugalkraft). Die fiktive Kraft ist in diesem Fall also in erster Linie eine gleichförmige Zentrifugalkraft entlang der Rohrachse, weg vom Rotationszentrum, mit einem Wert | F _Fikt | = ω ² R , wobei R der Abstand der Materie im Röhrchen vom Zentrum der Zentrifuge ist. Es ist die Standardspezifikation einer Zentrifuge, den "effektiven" Radius der Zentrifuge zu verwenden, um ihre Fähigkeit zur Bereitstellung der Zentrifugalkraft abzuschätzen. Somit kann eine erste Schätzung der Zentrifugalkraft in einer Zentrifuge auf dem Abstand der Röhrchen vom Rotationszentrum basieren und bei Bedarf Korrekturen vorgenommen werden.

Außerdem beschränkt das Teströhrchen die Bewegung auf die Richtung entlang der Länge des Röhrchens, so dass v _B entgegengesetzt zu u ₁ und die Corioliskraft entgegengesetzt zu u _{2 ist} , d. h. gegen die Wand des Röhrchens. Wird das Rohr lange genug gedreht, sinkt die Geschwindigkeit v _B auf Null, wenn die Materie eine Gleichgewichtsverteilung erreicht. Weitere Details finden Sie in den Artikeln zur Sedimentation und zur Lamm-Gleichung .

Ein verwandtes Problem sind die Zentrifugalkräfte für das Erde-Mond-Sonne-System, bei dem drei Rotationen auftreten: die tägliche Rotation der Erde um ihre Achse, die Mondmonatsrotation des Erde-Mond-Systems um ihren Massenschwerpunkt und die jährliche Umdrehung des Erde-Mond-Systems um die Sonne. Diese drei Bewegungen beeinflussen die Gezeiten .

Ein Karussell überqueren

Abbildung 5: Beim Überqueren eines rotierenden Karussells, das mit konstanter Geschwindigkeit von der Mitte des Karussells zu seinem Rand läuft, wird im Trägheitsrahmen eine Spirale gezogen, während im Rahmen des Karussells ein einfacher gerader radialer Weg zu sehen ist.

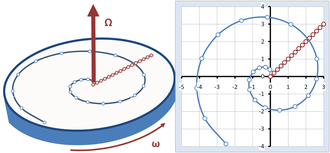
Abbildung 5 zeigt ein weiteres Beispiel, das die Beobachtungen eines Trägheitsbeobachters mit denen eines Beobachters auf einem rotierenden Karussell vergleicht . Das Karussell dreht sich mit einer konstanten Winkelgeschwindigkeit, die durch den Vektor Ω mit der Größe ω dargestellt wird und nach der Rechts-Hand-Regel nach oben zeigt . Ein Reiter auf dem Karussell läuft radial mit konstanter Geschwindigkeit darüber, was dem Wanderer in Abbildung 5 als geradliniger Weg erscheint, der in Abbildung 5 um 45° geneigt ist. Die auf beiden Pfaden in Fig. 5 identifizierten Punkte entsprechen den gleichen Zeiten, die in gleichen Zeitintervallen beabstandet sind. Wir fragen, wie zwei Beobachter, einer auf dem Karussell und einer in einem Trägheitsrahmen, das, was sie sehen, anhand der Newtonschen Gesetze formulieren.

Trägheitsbeobachter

Der ruhende Beobachter beschreibt den Weg des Wanderers als Spirale. Unter Annahme des in Abbildung 5 gezeigten Koordinatensystems wird die Trajektorie durch r ( t ) beschrieben:

${\displaystyle \mathbf {r} (t)=R(t)\mathbf {u} _{R}={\begin{bmatrix}x(t)\\y(t)\end{bmatrix}}={ \begin{bmatrix}R(t)\cos(\omega t+\pi/4)\\R(t)\sin(\omega t+\pi/4)\end{bmatrix}},}$

wobei das hinzugefügte π/4 den Wegwinkel zu Beginn auf 45° setzt (nur eine willkürliche Wahl der Richtung), u _R ist ein Einheitsvektor in radialer Richtung, der zum Zeitpunkt t vom Zentrum des Karussells zum Geher zeigt . Der radiale Abstand R ( t ) nimmt mit der Zeit stetig zu gemäß:

${\displaystyle R(t)=st,}$

mit s der Gehgeschwindigkeit. Nach einfacher Kinematik ist die Geschwindigkeit dann die erste Ableitung der Trajektorie:

${\displaystyle \mathbf {v} (t)={\frac {dR}{dt}}{\begin{bmatrix}\cos(\omega t+\pi/4)\\\sin(\omega t+\pi / 4)\end{bmatrix}}+\omega R(t){\begin{bmatrix}-\sin(\omega t+\pi/4)\\\cos(\omega t+\pi/4)\end{bmatrix }}}$

${\displaystyle ={\frac {dR}{dt}}\mathbf {u} _{R}+\omega R(t)\mathbf {u}_{\theta},}$

mit u _θ ein Einheitsvektor senkrecht zu u _R zum Zeitpunkt t (wie man verifizieren kann, indem man beachtet, dass das Vektorpunktprodukt mit dem radialen Vektor null ist) und in Fahrtrichtung zeigt. Die Beschleunigung ist die erste Ableitung der Geschwindigkeit:

${\displaystyle \mathbf {a} (t)={\frac {d^{2}R}{dt^{2}}}{\begin{bmatrix}\cos(\omega t+\pi/4)\\ \sin(\omega t+\pi/4)\end{bmatrix}}+2{\frac {dR}{dt}}\omega {\begin{bmatrix}-\sin(\omega t+\pi/4)\ \\cos(\omega t+\pi/4)\end{bmatrix}}-\omega ^{2}R(t){\begin{bmatrix}\cos(\omega t+\pi/4)\\\sin (\omega t+\pi/4)\end{bmatrix}}}$

${\displaystyle =2s\omega {\begin{bmatrix}-\sin(\omega t+\pi/4)\\\cos(\omega t+\pi/4)\end{bmatrix}}-\omega ^{2 }R(t){\begin{bmatrix}\cos(\omega t+\pi/4)\\\sin(\omega t+\pi/4)\end{bmatrix}}}$

${\displaystyle =2s\\omega\\mathbf{u}_{\theta}-\omega^{2}R(t)\\mathbf{u}_{R}\ .}$

Der letzte Term in der Beschleunigung liegt radial nach innen vom Betrag ω ² R , was also die momentane Zentripetalbeschleunigung der Kreisbewegung ist . Der erste Term steht senkrecht zur radialen Richtung und zeigt in Fahrtrichtung. Seine Größe beträgt 2 s ω und stellt die Beschleunigung des Wanderers dar, wenn sich der Rand des Karussells nähert und der in einer festen Zeit zurückgelegte Kreisbogen zunimmt, wie aus dem größeren Abstand zwischen den Punkten für gleiche Zeitschritte ersichtlich ist auf der Spirale in Abbildung 5, wenn man sich der Außenkante des Karussells nähert.

Wendet man die Newtonschen Gesetze an und multipliziert die Beschleunigung mit der Masse des Läufers, kommt der Trägheitsbeobachter zu dem Schluss, dass der Läufer zwei Kräften ausgesetzt ist: der nach innen gerichteten, radial gerichteten Zentripetalkraft und einer weiteren Kraft senkrecht zur radialen Richtung, die proportional zur Geschwindigkeit von . ist der Geher.

Rotierender Beobachter

Der rotierende Beobachter sieht, wie sich der Läufer eine gerade Linie von der Mitte des Karussells zum Rand bewegt, wie in Abbildung 5 gezeigt. Darüber hinaus sieht der rotierende Beobachter, dass sich der Läufer mit konstanter Geschwindigkeit in die gleiche Richtung bewegt, sodass das Newtonsche Gesetz von . angewendet wird Trägheit gibt es keine Kraft auf den Gehwagen. Diese Schlussfolgerungen stimmen nicht mit dem Trägheitsbeobachter überein. Um eine Übereinstimmung zu erzielen, muss der rotierende Beobachter fiktive Kräfte einführen, die in der rotierenden Welt zu existieren scheinen, obwohl es dafür keinen offensichtlichen Grund gibt, keine scheinbare Gravitationsmasse, elektrische Ladung oder was auch immer, die diese fiktiven Kräfte erklären könnten .

Um dem Trägheitsbeobachter zuzustimmen, müssen die auf den Geher ausgeübten Kräfte genau die oben genannten sein. Sie können auf die bereits abgeleiteten allgemeinen Formeln bezogen werden, nämlich:

${\displaystyle \mathbf {F} _{\mathrm {fikt} }=-2m{\boldsymbol {\Omega}}\times \mathbf {v} _{\mathrm {B}}-m{\boldsymbol {\Omega }}\times ({\boldsymbol {\Omega}}\times \mathbf {x}_{\mathrm {B}})-m{\frac {d{\boldsymbol {\Omega}}}{dt}}\ mal \mathbf{x}_{\mathrm{B}}.}$

In diesem Beispiel ist die im rotierenden Rahmen gesehene Geschwindigkeit:

${\displaystyle \mathbf{v}_{\textrm{B}}=s\mathbf{u}_{R},}$

mit u _R ein Einheitsvektor in radialer Richtung. Die Position des Rollators auf dem Karussell ist:

${\displaystyle\mathbf{x}_{\mathrm{B}}=R(t)\mathbf{u}_{R},}$

und die zeitliche Ableitung von Ω ist null für eine gleichförmige Winkeldrehung. Das merken

${\displaystyle {\boldsymbol {\Omega}}\times \mathbf{u}_{R}=\omega\mathbf{u}_{\theta}\}$

und

${\displaystyle {\boldsymbol {\Omega}}\times \mathbf {u} _{\theta}=-\omega \mathbf {u} _{R}\ ,}$

wir finden:

${\displaystyle \mathbf {F} _{\mathrm {fikt}}=-2m\omega s\mathbf {u} _{\theta}+m\omega ^{2}R(t)\mathbf {u} _ {R}.}$

Um eine geradlinige Bewegung in der rotierenden Welt zu erhalten, muss eine Kraft angewendet werden, die im Vorzeichen der fiktiven Kraft genau entgegengesetzt ist, um die Nettokraft auf den Läufer auf Null zu reduzieren, so dass das Newtonsche Trägheitsgesetz eine geradlinige Bewegung vorhersagt, in Übereinstimmung mit dem, was der rotierende Beobachter sieht. Die fiktiven Kräfte, die bekämpft werden müssen, sind die Corioliskraft (erster Term) und die Fliehkraft (zweiter Term). (Diese Begriffe sind Näherungswerte.) Durch das Aufbringen von Kräften, um diesen beiden fiktiven Kräften entgegenzuwirken, übt der rotierende Beobachter am Ende genau die gleichen Kräfte auf den Geher aus, die der Trägheitsbeobachter vorhergesagt hatte.

Da sie sich nur durch die konstante Gehgeschwindigkeit unterscheiden, sehen Geher und Rotationsbeobachter die gleichen Beschleunigungen. Aus der Sicht des Wanderers wird die fiktive Kraft als real erlebt, und es ist notwendig, diese Kraft zu bekämpfen, um auf einer geraden radialen Bahn mit konstanter Geschwindigkeit zu bleiben. Es ist, als würde man gegen einen Seitenwind kämpfen, während man an den Rand des Karussells geschleudert wird.

Überwachung

Beachten Sie, dass diese kinematische Diskussion nicht auf den Mechanismus eingeht, durch den die erforderlichen Kräfte erzeugt werden. Das ist das Thema der Kinetik . Im Fall des Karussells würde die kinetische Diskussion vielleicht eine Untersuchung der Schuhe des Wanderers und der Reibung, die sie gegen den Boden des Karussells erzeugen müssen, oder vielleicht die Dynamik des Skateboardens beinhalten, wenn der Wanderer auf das Skateboard umsteigt. Unabhängig von der Fortbewegungsart des Karussells müssen die oben berechneten Kräfte realisiert werden. Eine sehr grobe Analogie ist das Heizen Ihres Hauses: Sie müssen eine bestimmte Temperatur haben, um sich wohl zu fühlen, aber ob Sie mit Gas oder Kohle heizen, ist ein weiteres Problem. Kinematik stellt den Thermostat ein, Kinetik befeuert den Ofen.

Siehe auch

Anmerkungen

Weiterlesen

• Lev D. Landau und EM Lifshitz (1976). Mechanik . Studiengang Theoretische Physik . vol. 1 (3. Aufl.). Butterworth-Heinenan. S. 128–130. ISBN 0-7506-2896-0. |volume=hat zusätzlichen Text ( Hilfe )
• Keith Symon (1971). Mechanik (3. Aufl.). Addison-Wesley. ISBN 0-201-07392-7.
• Jerry B. Marion (1970). Klassische Dynamik von Teilchen und Systemen . Akademische Presse. ISBN 0-12-472252-0.
• Marcel J. Sidi (1997). Dynamik und Steuerung von Raumfahrzeugen: Ein praktischer technischer Ansatz . Cambridge University Press. Kapitel 4.8. ISBN 0-521-78780-7.

Externe Links

• Fragen und Antworten von Richard C. Brill, Honolulu Community College
• David Stern von der NASA: Unterrichtspläne für Lehrer Nr. 23 über Trägheitskräfte
• Corioliskraft
• Bewegung über eine flache Oberfläche Java-Physlet von Brian Fiedler zur Veranschaulichung fiktiver Kräfte. Das Physlet zeigt sowohl die Perspektive aus rotierender als auch aus nicht rotierender Sicht.
• Bewegung über einer parabolischen Oberfläche Java-Physlet von Brian Fiedler zur Veranschaulichung fiktiver Kräfte. Das Physlet zeigt sowohl die Perspektive aus rotierender als auch aus nicht rotierender Sicht.