Fourier-Reihe -Fourier series
| Fourier-Transformationen |
|---|
Eine Fourier - Reihe ( / ˈ f ʊr i eɪ , - i ər / ) ist eine Erweiterung einer periodischen Funktion in eine Summe trigonometrischer Funktionen . Die Fourier-Reihe ist ein Beispiel für eine trigonometrische Reihe , aber nicht alle trigonometrischen Reihen sind Fourier-Reihen. Durch das Ausdrücken einer Funktion als Summe von Sinus und Cosinus werden viele Probleme, die die Funktion betreffen, einfacher zu analysieren, da trigonometrische Funktionen gut verstanden werden. Zum Beispiel wurden Fourier-Reihen erstmals von Joseph Fourier verwendet , um Lösungen für die Wärmegleichung zu finden . Diese Anwendung ist möglich, weil die Ableitungen trigonometrischer Funktionen in einfache Muster fallen. Fourier-Reihen können nicht verwendet werden, um beliebige Funktionen zu approximieren, da die meisten Funktionen unendlich viele Terme in ihren Fourier-Reihen haben und die Reihen nicht immer konvergieren . Wohlverhaltende Funktionen, zum Beispiel glatte Funktionen, haben Fourier-Reihen, die gegen die ursprüngliche Funktion konvergieren. Die Koeffizienten der Fourier-Reihe werden durch Integrale der Funktion bestimmt, die mit trigonometrischen Funktionen multipliziert werden, wie unten in Allgemeine Formen der Fourier-Reihe beschrieben.
Die Untersuchung der Konvergenz von Fourier-Reihen konzentriert sich auf das Verhalten der Partialsummen , was bedeutet, dass das Verhalten der Summe untersucht wird, wenn immer mehr Terme aus der Reihe summiert werden. Die folgenden Abbildungen veranschaulichen einige Teilergebnisse der Fourier-Reihe für die Komponenten einer Rechteckwelle .
Eine Rechteckwelle (dargestellt als blauer Punkt) wird durch ihre sechste Partialsumme (dargestellt als violetter Punkt) angenähert, die durch Summieren der ersten sechs Terme (dargestellt als Pfeile) der Fourier-Reihe der Rechteckwelle gebildet wird. Jeder Pfeil beginnt bei der vertikalen Summe aller Pfeile zu seiner Linken (dh der vorherigen Teilsumme).
Die ersten vier Partialsummen der Fourier-Reihe für eine Rechteckwelle . Wenn mehr Harmonische hinzugefügt werden, konvergieren die Partialsummen zur Rechteckwelle (werden immer ähnlicher).
Fourier-Reihen sind eng mit der Fourier-Transformation verwandt , die verwendet werden kann, um die Frequenzinformationen für Funktionen zu finden, die nicht periodisch sind. Periodische Funktionen können mit Funktionen auf einem Kreis identifiziert werden, aus diesem Grund sind Fourier-Reihen Gegenstand der Fourier-Analyse auf einem Kreis, die normalerweise als oder bezeichnet werden . Die Fourier-Transformation ist ebenfalls Teil der Fourier-Analyse , ist aber für Funktionen weiter definiert
Seit Fourier wurden viele verschiedene Ansätze zur Definition und zum Verständnis des Konzepts der Fourier-Reihen entdeckt, die alle miteinander konsistent sind, aber jeweils unterschiedliche Aspekte des Themas betonen. Einige der leistungsfähigeren und eleganteren Ansätze basieren auf mathematischen Ideen und Werkzeugen, die zu Fouriers Zeiten nicht verfügbar waren. Fourier definierte ursprünglich die Fourier-Reihe für reellwertige Funktionen reeller Argumente und verwendete die Sinus- und Kosinusfunktionen bei der Zerlegung. Seitdem wurden viele andere Fourier-bezogene Transformationen definiert, die seine ursprüngliche Idee auf viele Anwendungen ausdehnten und einen Bereich der Mathematik namens Fourier-Analyse hervorbrachten .
Übliche Formen der Fourier-Reihe
Die Fourier-Reihe kann in verschiedenen Formen dargestellt werden. Die Sinus-Cosinus- Form, Exponentialform und Amplituden-Phasen- Form werden hier für eine periodische Funktion ausgedrückt .

Sinus-Cosinus-Form
Die Koeffizienten der Fourier-Reihe werden durch die Integrale definiert:
|
|
|
( Gl. 1 ) |
Es ist bemerkenswert, dass der Durchschnittswert der Funktion ist . Dies ist eine Eigenschaft, die sich auf ähnliche Transformationen wie die Fourier-Transformation erstreckt .
Mit diesen definierten Koeffizienten ist die Fourier-Reihe:
|
|
|
( Gl. 2 ) |
Viele andere verwenden das Symbol, weil es nicht immer stimmt, dass die Summe der Fourier-Reihe gleich ist . Es kann nicht vollständig konvergieren oder zu etwas konvergieren, das sich von unterscheidet . Während diese Situationen auftreten können, sind ihre Unterschiede in Wissenschaft und Technik selten ein Problem, und Autoren in diesen Disziplinen schreiben manchmal Gl. 2 mit ersetzt durch .
Der ganzzahlige Index in den Fourier-Reihenkoeffizienten ist die Anzahl der Zyklen, die die entsprechenden oder aus der Reihe in der Periode der Funktion machen . Daher entsprechen die Begriffe und haben:
- eine Wellenlänge gleich und mit den gleichen Einheiten wie .
- eine Frequenz gleich und mit reziproken Einheiten als .
Beispiel

Betrachten Sie eine Sägezahnfunktion:
In diesem Fall sind die Fourier-Koeffizienten gegeben durch
Es kann gezeigt werden, dass die Fourier-Reihe an jedem Punkt konvergiert, an dem differenzierbar ist, und daher:
-
( Gl.8 )
Wenn ein ungerades Vielfaches von ist , konvergiert die Fourier-Reihe gegen 0, was die Halbsumme der linken und rechten Grenze von s bei ist . Dies ist ein besonderer Fall des Dirichlet-Theorems für Fourier-Reihen.
Dieses Beispiel führt zu einer Lösung des Basler Problems .
Exponentialform
Es ist möglich, die Integrale für die Koeffizienten der Fourier-Reihe zu vereinfachen, indem man die Euler-Formel verwendet .
Mit den Definitionen
|
|
|
( Gl. 3 ) |
Durch Einsetzen von Gleichung Gl. 1 in Gl. 3 lässt sich zeigen:
Angesichts der Koeffizienten der komplexen Fourier-Reihe ist es möglich, und aus den Formeln zu gewinnen
Mit diesen Definitionen wird die Fourier-Reihe geschrieben als:
|
|
|
( Gl. 4 ) |
Dies ist die übliche Form für die Verallgemeinerung auf komplexwertige Funktionen. Negative Werte von entsprechen einer negativen Frequenz . (Siehe auch Fourier-Transformation § Negative Frequenz ).
Amplituden-Phasen-Form
Die Fourier-Reihe in Amplituden - Phasen- Form ist:
|
|
|
( Gl. 5 ) |
- Seine Harmonische ist .
- ist die Amplitude der Harmonischen und ihre Phasenverschiebung .
- Die Grundfrequenz von ist der Begriff für wenn gleich 1 und kann als Harmonische bezeichnet werden .
- wird manchmal als harmonische oder DC-Komponente bezeichnet . Es ist der Mittelwert von .
Gl . 5 kann Funktionen darstellen, die nur eine Summe von einer oder mehreren der harmonischen Frequenzen sind. Das Bemerkenswerte für diejenigen, die mit diesem Konzept noch nicht vertraut sind, ist, dass es aufgrund der potenziell unendlichen Anzahl von Termen ( ) auch die Zwischenfrequenzen und/oder Nicht-Sinusfunktionen darstellen kann .

Die Koeffizienten und können als Kreuzkorrelation zwischen und einer Sinuskurve bei der Frequenz verstanden und abgeleitet werden . Für eine allgemeine Häufigkeit und ein Analyseintervall gilt die Kreuzkorrelationsfunktion:
|
|
|
( Gl. 6 ) |
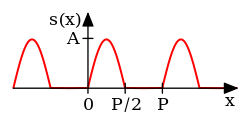
ist im Wesentlichen ein angepasster Filter mit Vorlage . Hier bedeutet Wenn ist -periodisch, ist willkürlich, oft als oder gewählt Aber im Allgemeinen kann die Fourier-Reihe auch verwendet werden, um eine nichtperiodische Funktion auf nur einem endlichen Intervall darzustellen, wie in Abb.1 dargestellt.
Das Maximum von ist ein Maß für die Amplitude der Frequenz in der Funktion , und der Wert von beim Maximum bestimmt die Phase dieser Frequenz. Fig. 2 ist ein Beispiel, wobei eine Rechteckwelle (nicht gezeigt) und die Frequenz die Harmonische ist . Es ist auch ein Beispiel dafür, das Maximum aus nur zwei Abtastungen abzuleiten, anstatt die gesamte Funktion zu durchsuchen. Dies wird durch eine trigonometrische Identität ermöglicht :
Kombiniert man dies mit Gl. 6 ergibt:
die die Definitionen von und einführt . Und wir merken zur späteren Referenz an, dass und vereinfacht werden kann:
Daher sind und die rechtwinkligen Koordinaten eines Vektors mit Polarkoordinaten und
Erweiterungen zu nicht periodischen Funktionen
Fourier-Reihen können auch auf Funktionen angewendet werden, die nicht notwendigerweise periodisch sind. Die einfachste Erweiterung ergibt sich, wenn die Funktion nur in einem festen Intervall definiert wird . In diesem Fall können die die Fourier-Koeffizienten definierenden Integrale über dieses Intervall genommen werden. In diesem Fall sind alle Konvergenzergebnisse die gleichen wie bei der periodischen Erweiterung von auf die gesamte reelle Linie. Insbesondere kann es vorkommen, dass bei einer stetigen Funktion eine Diskontinuität in der periodischen Verlängerung von at und auftritt . In diesem Fall ist es möglich, das Gibbs-Phänomen an den Endpunkten des Intervalls zu sehen .
Für Funktionen mit kompakter Unterstützung , was bedeutet, dass Werte von überall definiert sind, aber außerhalb eines festen Intervalls identisch Null sind , kann die Fourier-Reihe auf jedem Intervall genommen werden, das die Unterstützung enthält .
Für beide oben genannten Fälle ist es manchmal wünschenswert, eine gerade oder ungerade Spiegelung der Funktion zu nehmen oder sie um Null zu erweitern, falls die Funktion nur in einem endlichen Intervall definiert ist. Damit können den Fourier-Koeffizienten gewünschte Eigenschaften vorgegeben werden. Indem Sie zum Beispiel die Funktion selbst machen, stellen Sie sicher, dass . Dies wird oft als Kosinusreihe bezeichnet . Ebenso kann man zu einer Sinusreihe kommen.
In dem Fall, in dem die Funktion keine kompakte Unterstützung hat und auf der gesamten reellen Linie definiert ist, kann man die Fourier-Transformation verwenden . Fourier-Reihen können für eine abgeschnittene Version der Funktion oder für die periodische Summation verwendet werden .
Teilsummenoperator
Wenn Autoren beschreiben, wie sich Fourier-Reihen verhalten, führen sie häufig den Partialsummenoperator für eine Funktion ein .
|
|
|
( Gl. 8 ) |
Wo sind die Fourier-Koeffizienten von . Im Gegensatz zu Reihen in der Analysis ist es wichtig, dass die Partialsummen für Fourier-Reihen symmetrisch genommen werden, da sonst die Konvergenzergebnisse möglicherweise nicht gelten.
Konvergenz
Ein Beweis, dass eine Fourier-Reihe eine gültige Darstellung einer beliebigen periodischen Funktion ist (die die Dirichlet-Bedingungen erfüllt ), wird in § Fourier-Theorem, das die Konvergenz von Fourier-Reihen beweist, zusammengefasst .
In technischen Anwendungen wird im Allgemeinen angenommen, dass die Fourier-Reihe konvergiert, außer an Sprungdiskontinuitäten, da sich die in der Technik angetroffenen Funktionen besser verhalten als Funktionen, die in anderen Disziplinen angetroffen werden. Insbesondere wenn stetig ist und die Ableitung von (die möglicherweise nicht überall existiert) quadratisch integrierbar ist, dann konvergiert die Fourier-Reihe von absolut und gleichmäßig gegen . Wenn eine Funktion auf dem Intervall quadratintegrierbar ist, dann konvergiert die Fourier-Reihe fast überall gegen die Funktion . Es ist möglich, Fourier-Koeffizienten für allgemeinere Funktionen oder Verteilungen zu definieren, wobei in diesem Fall die punktweise Konvergenz häufig fehlschlägt und normalerweise die Konvergenz in der Norm oder die schwache Konvergenz untersucht wird.
Vier Teilsummen (Fourier-Reihen) der Längen 1, 2, 3 und 4 Glieder, die zeigen, wie sich die Annäherung an eine Rechteckwelle mit zunehmender Anzahl von Gliedern verbessert (Animation)
Vier Teilsummen (Fourier-Reihen) der Längen 1, 2, 3 und 4 Glieder, die zeigen, wie sich die Annäherung an eine Sägezahnwelle mit zunehmender Anzahl von Gliedern verbessert (Animation)
Beispiel für Konvergenz zu einer etwas willkürlichen Funktion. Beachten Sie die Entwicklung des „Klingelns“ ( Gibbs-Phänomen ) an den Übergängen zu/von den vertikalen Abschnitten.
Andere gebräuchliche Notationen
Die Notation ist unzureichend, um die Fourier-Koeffizienten mehrerer verschiedener Funktionen zu diskutieren. Daher wird es üblicherweise durch eine modifizierte Form der Funktion ( in diesem Fall ) ersetzt, wie z. B. oder , und die funktionale Notation ersetzt häufig die Subskription:
In der Technik wird die Koeffizientenfolge insbesondere dann, wenn die Variable die Zeit darstellt, als Frequenzbereichsdarstellung bezeichnet . Eckige Klammern werden oft verwendet, um zu betonen, dass die Domäne dieser Funktion ein diskreter Satz von Frequenzen ist.
Eine andere häufig verwendete Frequenzbereichsdarstellung verwendet die Koeffizienten der Fourier-Reihe, um einen Dirac-Kamm zu modulieren :
wobei einen kontinuierlichen Frequenzbereich darstellt. Wenn Variable Einheiten von Sekunden hat, hat Einheiten von Hertz . Die "Zähne" des Kamms sind bei Vielfachen (dh Harmonischen ) von beabstandet, was die Grundfrequenz genannt wird . kann aus dieser Darstellung durch eine inverse Fourier-Transformation wiedergewonnen werden :
Die konstruierte Funktion wird daher allgemein als Fourier-Transformation bezeichnet , obwohl das Fourier-Integral einer periodischen Funktion bei den harmonischen Frequenzen nicht konvergiert.
Geschichte
Die Fourier-Reihe ist nach Voruntersuchungen von Leonhard Euler , Jean le Rond d'Alembert und Daniel Bernoulli zu Ehren von Jean-Baptiste Joseph Fourier (1768–1830) benannt, der wichtige Beiträge zum Studium trigonometrischer Reihen geleistet hat . Fourier führte die Reihe ein, um die Wärmegleichung in einer Metallplatte zu lösen, veröffentlichte seine ersten Ergebnisse 1807 in seinem Mémoire sur la propagation de la chaleur dans les corps solides ( Abhandlung über die Ausbreitung von Wärme in festen Körpern ) und veröffentlichte seine Théorie analytique de la chaleur ( Analytische Theorie der Wärme ) im Jahr 1822. Das Mémoire führte die Fourier-Analyse ein, insbesondere Fourier-Reihen. Durch Fouriers Forschung wurde die Tatsache festgestellt, dass eine beliebige (zunächst stetige und später verallgemeinert zu jeder stückweise glatten) Funktion durch eine trigonometrische Reihe dargestellt werden kann. Die erste Ankündigung dieser großen Entdeckung wurde 1807 von Fourier vor der französischen Akademie gemacht . Frühe Ideen, eine periodische Funktion in die Summe einfacher oszillierender Funktionen zu zerlegen, gehen auf das 3. Jahrhundert v. Chr. zurück, als alte Astronomen ein empirisches Modell der Planetenbewegungen vorschlugen, das auf Deferenten und Epizykeln basierte .
Die Wärmegleichung ist eine partielle Differentialgleichung . Vor Fouriers Arbeit war im allgemeinen Fall keine Lösung der Wärmegleichung bekannt, obwohl bestimmte Lösungen bekannt waren, wenn sich die Wärmequelle auf einfache Weise verhielt, insbesondere wenn die Wärmequelle eine Sinus- oder Cosinuswelle war . Diese einfachen Lösungen werden heute manchmal als Eigenlösungen bezeichnet . Fouriers Idee war es, eine komplizierte Wärmequelle als Überlagerung (oder Linearkombination ) einfacher Sinus- und Kosinuswellen zu modellieren und die Lösung als Überlagerung der entsprechenden Eigenlösungen zu schreiben . Diese Überlagerung oder Linearkombination wird als Fourier-Reihe bezeichnet.
Aus heutiger Sicht sind Fouriers Ergebnisse aufgrund des Fehlens eines genauen Begriffs von Funktion und Integral im frühen 19. Jahrhundert etwas informell. Später drückten Peter Gustav Lejeune Dirichlet und Bernhard Riemann Fouriers Ergebnisse mit größerer Präzision und Formalität aus.
Obwohl die ursprüngliche Motivation darin bestand, die Wärmegleichung zu lösen, wurde später klar, dass dieselben Techniken auf eine Vielzahl mathematischer und physikalischer Probleme angewendet werden können, insbesondere auf solche mit linearen Differentialgleichungen mit konstanten Koeffizienten, für die die Eigenlösungen Sinuskurven sind . Die Fourier-Reihe hat viele solcher Anwendungen in der Elektrotechnik , Schwingungsanalyse , Akustik , Optik , Signalverarbeitung , Bildverarbeitung , Quantenmechanik , Ökonometrie , Schalentheorie usw.
Anfänge
Josef Fourier schrieb:
Beide Seiten mit multiplizieren und dann von bis integrieren ergibt:
— Joseph Fourier, Mémoire sur la propagation de la chaleur dans les corps solides . (1807)
Daraus ergibt sich sofort jeder Koeffizient a k der trigonometrischen Reihe für φ( y ) für jede Funktion, die eine solche Entwicklung hat. Es funktioniert, denn wenn φ eine solche Erweiterung hat, dann (unter geeigneten Konvergenzannahmen) das Integral
In diesen wenigen Zeilen, die dem modernen Formalismus der Fourier-Reihen nahe kommen , hat Fourier sowohl die Mathematik als auch die Physik revolutioniert. Obwohl ähnliche trigonometrische Reihen zuvor von Euler , d'Alembert , Daniel Bernoulli und Gauss verwendet wurden , glaubte Fourier, dass solche trigonometrischen Reihen jede beliebige Funktion darstellen könnten. Inwiefern das tatsächlich zutrifft, ist eine etwas subtile Frage, und die jahrelangen Versuche, diese Idee zu klären, haben zu wichtigen Entdeckungen in den Theorien der Konvergenz , der Funktionsräume und der harmonischen Analyse geführt .
Als Fourier 1811 einen späteren Wettbewerbsaufsatz einreichte, kam das Komitee (dem unter anderem Lagrange , Laplace , Malus und Legendre angehörten) zu dem Schluss: ... die Art und Weise, wie der Autor zu diesen Gleichungen gelangt, ist nicht frei von Schwierigkeiten und ... seine Analyse, sie zu integrieren, lässt in puncto Allgemeingültigkeit und sogar Strenge noch zu wünschen übrig .
Fouriers Motivation
Die Fourier-Reihenentwicklung der Sägezahnfunktion (oben) sieht komplizierter aus als die einfache Formel , daher ist nicht sofort ersichtlich, warum man die Fourier-Reihe benötigen würde. Obwohl es viele Anwendungen gibt, lag Fouriers Motivation darin, die
Wärmegleichung zu lösen . Stellen Sie sich zum Beispiel eine Metallplatte in Form eines Quadrats vor, dessen Seiten Meter messen, mit den Koordinaten . Wenn es keine Wärmequelle innerhalb der Platte gibt und wenn drei der vier Seiten auf 0 Grad Celsius gehalten werden, während die vierte Seite, gegeben durch , auf dem Temperaturgradienten Grad Celsius gehalten wird, für in , dann kann man zeigen, dass die Die stationäre Wärmeverteilung (oder die Wärmeverteilung nach Ablauf einer langen Zeitspanne) ist gegeben durchDabei ist sinh die hyperbolische Sinusfunktion . Diese Lösung der Wärmegleichung wird erhalten, indem jeder Term von Gleichung 6 mit multipliziert wird . Während unsere Beispielfunktion eine unnötig komplizierte Fourier-Reihe zu haben scheint, ist die Wärmeverteilung nicht trivial. Die Funktion kann nicht als
geschlossener Ausdruck geschrieben werden . Diese Methode zur Lösung des Wärmeproblems wurde durch Fouriers Arbeit ermöglicht.Komplexe Fourier-Reihenanimation
Ein Beispiel für die Fähigkeit der komplexen Fourier-Reihe, jede zweidimensionale geschlossene Figur nachzuzeichnen, ist in der nebenstehenden Animation der komplexen Fourier-Reihe gezeigt, die den Buchstaben „e“ (für Exponential) nachzeichnet. Beachten Sie, dass die Animation die Variable „t“ verwendet, um den Buchstaben „e“ in der komplexen Ebene zu parametrisieren, was der Verwendung des Parameters „x“ im Unterabschnitt dieses Artikels zu komplexwertigen Funktionen entspricht.
In der hinteren Ebene der Animation werden die rotierenden Vektoren in einer Reihenfolge aggregiert, die zwischen einem Vektor, der sich in positiver Richtung (gegen den Uhrzeigersinn) dreht, und einem Vektor, der sich mit derselben Frequenz, aber in negativer Richtung (im Uhrzeigersinn) dreht, abwechselt, was zu einer einzigen Verfolgung führt Arm mit vielen Zickzacks. Diese Perspektive zeigt, wie die Addition jedes Paares rotierender Vektoren (einer rotiert in positiver Richtung und einer rotiert in negativer Richtung) die vorherige Spur (dargestellt als hellgraue gepunktete Linie) näher an die Form des Buchstabens „e“ bringt. .
In der vorderen Ebene der Animation werden die rotierenden Vektoren in zwei Sätze aggregiert, den Satz aller positiven rotierenden Vektoren und den Satz aller negativen rotierenden Vektoren (die nicht rotierende Komponente wird gleichmäßig zwischen den beiden aufgeteilt), was zu zwei Verfolgungen führt Arme drehen sich in entgegengesetzte Richtungen. Der kleine Kreis der Animation bezeichnet den Mittelpunkt zwischen den beiden Armen und auch den Mittelpunkt zwischen dem Ursprung und dem aktuellen Verfolgungspunkt, der mit „+“ gekennzeichnet ist. Diese Perspektive zeigt, wie die komplexe Fourier-Reihe eine Erweiterung (das Hinzufügen eines Arms) der komplexen geometrischen Reihe ist, die nur einen Arm hat. Es zeigt auch, wie die beiden Arme miteinander koordinieren. Wenn sich beispielsweise der Verfolgungspunkt in die positive Richtung dreht, bleibt der Arm der negativen Richtung geparkt. Wenn sich der Verfolgungspunkt in der negativen Richtung dreht, bleibt der Arm für die positive Richtung in ähnlicher Weise geparkt.
Zwischen den hinteren und vorderen Ebenen der Animation befinden sich rotierende Trapeze, deren Flächen die Werte der komplexen Fourier-Reihenterme darstellen. Diese Perspektive zeigt die Amplitude, Frequenz und Phase der einzelnen Terme der komplexen Fourier-Reihe in Bezug auf die Reihensumme, die räumlich zum Buchstaben 'e' in der hinteren und vorderen Ebene konvergiert. Der linke und der rechte Kanal der Audiospur entsprechen jeweils den reellen und imaginären Komponenten des aktuellen Verfolgungspunkts „+“, jedoch in der Frequenz um den Faktor 3536 erhöht, sodass die Grundfrequenz der Animation (n=1) ein 220-Hz-Ton (A220 ).
Andere Anwendungen
Eine weitere Anwendung ist die Lösung des Basel-Problems mit Hilfe des Satzes von Parseval . Das Beispiel verallgemeinert und man kann ζ (2 n ) für jede positive ganze Zahl n berechnen .
Tabelle gängiger Fourier-Reihen
Einige gebräuchliche Paare periodischer Funktionen und ihre Fourier-Reihenkoeffizienten sind in der folgenden Tabelle aufgeführt.
- bezeichnet eine periodische Funktion mit period .
- bezeichnen die Fourier-Reihen-Koeffizienten (Sinus-Cosinus-Form) der periodischen Funktion .
| Zeitbereich |
Parzelle | Frequenzbereich (Sinus-Cosinus-Form) |
Bemerkungen | Referenz |
|---|---|---|---|---|
| Vollweggleichgerichteter Sinus | ||||
| Halbwellengleichgerichteter Sinus | ||||
Tabelle der Grundeigenschaften
Diese Tabelle zeigt einige mathematische Operationen im Zeitbereich und den entsprechenden Effekt in den Koeffizienten der Fourier-Reihe. Notation:
- Komplexe Konjugation wird durch ein Sternchen gekennzeichnet.
- bezeichnen -periodische Funktionen
| Eigentum | Zeitbereich | Frequenzbereich (exponentielle Form) | Bemerkungen | Referenz |
|---|---|---|---|---|
| Linearität | ||||
| Zeitumkehr / Frequenzumkehr | ||||
| Zeitkonjugation | ||||
| Zeitumkehr & Konjugation | ||||
| Realteil in der Zeit | ||||
| Imaginärer Teil der Zeit | ||||
| Realteil der Frequenz | ||||
| Imaginärer Teil der Frequenz | ||||
| Zeitverschiebung / Frequenzmodulation | ||||
| Frequenzverschiebung / Zeitmodulation |
Symmetrieeigenschaften
Wenn die Real- und Imaginärteile einer komplexen Funktion in ihre geraden und ungeraden Teile zerlegt werden , gibt es vier Komponenten, die unten durch die Indizes RE, RO, IE und IO gekennzeichnet sind. Und es gibt eine Eins-zu-Eins-Abbildung zwischen den vier Komponenten einer komplexen Zeitfunktion und den vier Komponenten ihrer komplexen Frequenztransformation:
Daraus ergeben sich verschiedene Zusammenhänge, zum Beispiel:
- Die Transformation einer reellwertigen Funktion ( s RE + s RO ) ist die gerade symmetrische Funktion S RE + i S IO . Umgekehrt impliziert eine geradsymmetrische Transformation einen reellwertigen Zeitbereich.
- Die Transformation einer imaginärwertigen Funktion ( i s IE + i s IO ) ist die ungerade symmetrische Funktion S RO + i S IE , und das Gegenteil ist wahr.
- Die Transformation einer geradsymmetrischen Funktion ( s RE + i s IO ) ist die reellwertige Funktion S RE + S RO , und das Gegenteil ist wahr.
- Die Transformation einer ungeradzahligen symmetrischen Funktion ( s RO + i s IE ) ist die imaginärwertige Funktion i S IE + i S IO , und das Gegenteil ist wahr.
Andere Eigenschaften
Riemann-Lebesgue-Lemma
If ist
integrierbar , , und Dieses Ergebnis ist als Riemann-Lebesgue-Lemma bekannt .Satz von Parseval
Wenn gehört zu (periodisch über ein Intervall der Länge ) dann
:Wenn zu (periodisch über ein Intervall der Länge ) gehört und von endlicher Länge ist , dann gilt :
denn dann
und für dann
Satz von Plancherel
Wenn Koeffizienten sind und dann gibt es eine eindeutige Funktion, so dass für jeden .
Faltungssätze
Gegeben -periodische Funktionen und mit Fourier-Reihenkoeffizienten und
- Das punktweise Produkt : ist auch -periodisch, und seine Fourier-Reihenkoeffizienten sind durch die diskrete Faltung der und -Sequenzen gegeben :
- Die periodische Faltung : ist auch -periodisch, mit Fourier-Reihenkoeffizienten :
- Eine doppelt unendliche Folge in ist die Folge von Fourier-Koeffizienten einer Funktion in genau dann, wenn sie eine Faltung zweier Folgen in ist . Sehen
Abgeleitetes Eigentum
Wir sagen, das gehört dazu , wenn eine 2 π -periodische Funktion ist, nach der Zeiten differenzierbar sind und deren Ableitung stetig ist.
- Wenn , dann können die Fourier - Koeffizienten der Ableitung durch die Fourier - Koeffizienten der Funktion über die Formel ausgedrückt werden .
- Wenn , dann . Da wir für ein festes haben , folgt insbesondere, dass gegen Null tendiert, was bedeutet, dass die Fourier-Koeffizienten schneller gegen Null konvergieren als die k- te Potenz von n für jedes .
Kompakte Gruppen
Eine der interessanten Eigenschaften der Fourier-Transformation, die wir erwähnt haben, ist, dass sie Faltungen zu punktweisen Produkten überträgt. Wenn dies die Eigenschaft ist, die wir bewahren wollen, kann man Fourier-Reihen über jede kompakte Gruppe erzeugen . Typische Beispiele umfassen jene klassischen Gruppen , die kompakt sind. Dies verallgemeinert die Fourier-Transformation auf alle Räume der Form L 2 ( G ), wobei G eine kompakte Gruppe ist, derart, dass die Fourier-Transformation Faltungen zu punktweisen Produkten trägt. Die Fourier-Reihe existiert und konvergiert auf ähnliche Weise wie im [− π , π ] -Fall.
Eine alternative Erweiterung kompakter Gruppen ist das Peter-Weyl-Theorem , das Ergebnisse über Darstellungen kompakter Gruppen analog zu denen über endliche Gruppen beweist.

Riemannsche Mannigfaltigkeiten
Wenn die Domäne keine Gruppe ist, dann gibt es keine intrinsisch definierte Faltung. Wenn jedoch eine kompakte Riemannsche Mannigfaltigkeit ist , hat sie einen Laplace-Beltrami-Operator . Der Laplace-Beltrami-Operator ist der Differentialoperator, der dem Laplace-Operator für die Riemannsche Mannigfaltigkeit entspricht . Dann kann man analog Wärmegleichungen auf betrachten . Da Fourier zu seiner Basis kam, indem er versuchte, die Wärmegleichung zu lösen, besteht die natürliche Verallgemeinerung darin, die Eigenlösungen des Laplace-Beltrami-Operators als Grundlage zu verwenden. Dies verallgemeinert Fourier-Reihen auf Räume des Typs , wobei eine Riemannsche Mannigfaltigkeit ist. Die Fourier-Reihe konvergiert auf ähnliche Weise wie der Fall. Als typisches Beispiel ist die Kugel mit der üblichen Metrik zu nehmen, in diesem Fall besteht die Fourier-Basis aus sphärischen Harmonischen .
Lokal kompakte abelsche Gruppen
Die oben diskutierte Verallgemeinerung auf kompakte Gruppen lässt sich nicht auf nichtkompakte, nichtabelsche Gruppen verallgemeinern . Es gibt jedoch eine einfache Verallgemeinerung auf Locally Compact Abelian (LCA)-Gruppen.
Dies verallgemeinert die Fourier-Transformation zu oder , wobei eine LCA-Gruppe ist. Wenn kompakt ist, erhält man auch eine Fourier-Reihe, die ähnlich wie der Fall konvergiert, aber wenn nicht kompakt ist, erhält man stattdessen ein Fourier-Integral . Diese Verallgemeinerung ergibt die übliche Fourier-Transformation , wenn die zugrunde liegende lokal kompakte abelsche Gruppe ist .
Erweiterungen
Fourierreihe auf einem Quadrat
Wir können die Fourier-Reihe auch für Funktionen von zwei Variablen und im Quadrat definieren :
Abgesehen davon, dass sie zum Lösen partieller Differentialgleichungen wie der Wärmegleichung nützlich ist, ist eine bemerkenswerte Anwendung der Fourier-Reihe auf dem Quadrat die Bildkomprimierung . Insbesondere verwendet der JPEG- Bildkomprimierungsstandard die zweidimensionale diskrete Kosinustransformation , eine diskrete Form der Fourier-Kosinustransformation , die nur den Kosinus als Basisfunktion verwendet.
Bei zweidimensionalen Arrays mit versetztem Erscheinungsbild verschwindet die Hälfte der Koeffizienten der Fourier-Reihe aufgrund zusätzlicher Symmetrie.
Fourier-Reihe der Bravais-Gitter-Periodik-Funktion
Ein dreidimensionales Bravais-Gitter ist definiert als der Satz von Vektoren der Form:
Damit können wir eine neue Funktion definieren,
Diese neue Funktion , ist jetzt eine Funktion von drei Variablen, von denen jede die Periodizität , , bzw. hat :
Dies ermöglicht es uns, einen Satz von Fourier-Koeffizienten aufzubauen, die jeweils durch drei unabhängige ganze Zahlen indiziert sind . Im Folgenden verwenden wir die Funktionsnotation, um diese Koeffizienten zu bezeichnen, wo wir zuvor Indizes verwendet haben. Wenn wir eine Reihe für auf das Intervall für schreiben , können wir Folgendes definieren:
Und dann können wir schreiben:
Weitere Definition:
Wir können noch einmal schreiben als:
Schließlich wenden wir dasselbe für die dritte Koordinate an und definieren:
Wir schreiben als:
Neuordnung:
Nun kann jeder reziproke Gittervektor geschrieben werden (was aber nicht bedeutet, dass dies die einzige Schreibweise ist) als , wobei ganze Zahlen sind und reziproke Gittervektoren zu erfüllen sind ( for , und for ). Dann ist für jeden beliebigen reziproken Gittervektor und beliebigen Positionsvektor im ursprünglichen Bravais-Gitterraum ihr Skalarprodukt:
Es ist also klar, dass in unserer Erweiterung von tatsächlich die Summe über reziproken Gittervektoren liegt:
Wo
Vorausgesetzt
(Es kann aus Gründen der Rechenvereinfachung von Vorteil sein, in einem solchen rechtwinkligen Koordinatensystem zu arbeiten, bei dem es zufälligerweise parallel zur
x- Achse ist, in der xy -Ebene liegt und Komponenten aller drei Achsen hat) . Der Nenner ist genau das Volumen der primitiven Einheitszelle, die von den drei primitiven Vektoren , und eingeschlossen wird . Vor allem das wissen wir jetztWir können jetzt als Integral mit dem traditionellen Koordinatensystem über das Volumen der primitiven Zelle schreiben, anstatt mit den Variablen , und :
Interpretation des Hilbertraums
In der Sprache der Hilbert-Räume ist die Menge der Funktionen eine
orthonormale Basis für den Raum der quadratintegrierbaren Funktionen auf . Dieser Raum ist eigentlich ein Hilbert-Raum mit einem inneren Produkt, das für zwei beliebige Elemente gegeben ist und durch:- wo ist das komplexe Konjugat von
Das grundlegende Ergebnis der Fourier-Reihe für Hilbert-Räume kann geschrieben werden als

Dies entspricht genau der oben angegebenen komplexen Exponentialformulierung. Auch die Version mit Sinus und Cosinus ist mit der Hilbertrauminterpretation begründet. Tatsächlich bilden die Sinus- und Cosinus-Werte eine orthogonale Menge :
Fourier-Theorem, das die Konvergenz von Fourier-Reihen beweist
Diese Theoreme und informelle Variationen davon, die die Konvergenzbedingungen nicht spezifizieren, werden manchmal allgemein als Fourier-Theorem oder Fourier-Theorem bezeichnet .
Die frühere Gl.7
Eigenschaft der kleinsten Quadrate
Der Satz von Parseval impliziert, dass:
Theorem — Das trigonometrische Polynom ist das eindeutig beste trigonometrische Polynom vom Grad, das approximiert , in dem Sinne, dass wir für jedes trigonometrische Polynom vom Grad haben:
Konvergenzsätze
Wegen der Eigenschaft der kleinsten Quadrate und wegen der Vollständigkeit der Fourier-Basis erhalten wir ein elementares Konvergenzergebnis.
Satz — Wenn zu (einem Intervall der Länge ) gehört, dann konvergiert zu in , das heißt, konvergiert gegen 0 als .
Wir haben bereits erwähnt, dass wenn stetig differenzierbar ist, then der Fourier-Koeffizient der Ableitung ist . Daraus folgt im Wesentlichen aus der
Cauchy-Schwarz-Ungleichung , dass absolut summierbar ist. Die Summe dieser Reihe ist eine stetige Funktion, gleich , da die Fourier-Reihe im Mittel gegen konvergiert :Satz — Wenn , dann konvergiert gegen gleichmäßig (und damit auch punktweise .)
Dieses Ergebnis lässt sich leicht beweisen, wenn weiter angenommen wird , da in diesem Fall als gegen Null tendiert . Allgemeiner gesagt ist die Fourier-Reihe absolut summierbar, konvergiert also gleichmäßig gegen , vorausgesetzt, dass eine
Hölder-Bedingung der Ordnung erfüllt ist . Im absolut summierbaren Fall gilt die Ungleichung:beweist gleichmäßige Konvergenz.
Es sind viele andere Ergebnisse zur Konvergenz von Fourier-Reihen bekannt, die von dem mäßig einfachen Ergebnis, dass die Reihe konvergiert, wenn sie differenzierbar ist , bis zu
Lennart Carlesons viel anspruchsvollerem Ergebnis, dass die Fourier-Reihe einer Funktion tatsächlich fast überall konvergiert, reichen .Abweichungen
Da Fourier-Reihen so gute Konvergenzeigenschaften haben, sind viele oft von einigen der negativen Ergebnisse überrascht. Beispielsweise muss die Fourier-Reihe einer kontinuierlichen T -periodischen Funktion nicht punktweise konvergieren. Das einheitliche Beschränktheitsprinzip liefert einen einfachen nicht-konstruktiven Beweis dieser Tatsache.
1922 veröffentlichte Andrey Kolmogorov einen Artikel mit dem Titel Une série de Fourier-Lebesgue divergente presque partout, in dem er ein Beispiel einer Lebesgue-integrierbaren Funktion gab, deren Fourier-Reihe fast überall divergiert. Später konstruierte er ein Beispiel einer integrierbaren Funktion, deren Fourier-Reihe überall divergiert ( Katznelson 1976 ).
Siehe auch
- ATS-Theorem
- Dirichlet-Kern
- Diskrete Fourier-Transformation
- Schnelle Fourier-Transformation
- Satz von Fejér
- Fourier-Analyse
- Fourier-Sinus- und Cosinus-Reihen
- Fourier-Transformation
- Gibbs-Phänomen
- Halbbereichs-Fourier-Reihe
- Laurent-Reihe – die Substitution q = e ix verwandelt eine Fourier-Reihe in eine Laurent-Reihe oder umgekehrt. Dies wird in der q -Reihenerweiterung der j -Invariante verwendet .
- Spektralanalyse der kleinsten Quadrate
- Mehrdimensionale Transformation
- Spektraltheorie
- Sturm-Liouville-Theorie
- Restsatzintegrale von f ( z ), Singularitäten, Pole
Anmerkungen
Verweise
Weiterlesen
- William E. Boyce; Richard C. DiPrima (2005). Elementare Differentialgleichungen und Grenzwertprobleme (8. Aufl.). New Jersey: John Wiley & Sons, Inc. ISBN 0-471-43338-1.
- Joseph Fourier, übersetzt von Alexander Freeman (2003). Die analytische Theorie der Wärme . Dover-Veröffentlichungen. ISBN 0-486-49531-0.2003 ungekürzte Neuveröffentlichung der englischen Übersetzung von Alexander Freeman von 1878 von Fouriers Werk Théorie Analytique de la Chaleur , das ursprünglich 1822 veröffentlicht wurde.
- Enrique A. González-Velasco (1992). "Verbindungen in der mathematischen Analyse: Der Fall der Fourier-Reihe". American Mathematical Monthly . 99 (5): 427–441. doi : 10.2307/2325087 . JSTOR2325087 . _
- Fetter, Alexander L.; Walecka, John Dirk (2003). Theoretische Mechanik von Teilchen und Kontinua . Kurier. ISBN 978-0-486-43261-8.
- Felix Klein , Entwicklung der Mathematik im 19. Jahrhundert . Mathsci Press Brookline, Mass, 1979. Übersetzt von M. Ackermann aus Vorlesungen über die Entwicklung der Mathematik im 19. Jahrhundert , Springer, Berlin, 1928.
- Walter Rudin (1976). Prinzipien der mathematischen Analyse (3. Aufl.). New York: McGraw-Hill, Inc. ISBN 0-07-054235-X.
- A. Zygmund (2002). Trigonometrische Reihe (dritte Aufl.). Cambridge: Cambridge University Press. ISBN 0-521-89053-5.Die Erstausgabe erschien 1935.
Externe Links
- "Fourier-Reihe" , Encyclopedia of Mathematics , EMS Press , 2001 [1994]
- Hobson, Ernst (1911). . Encyclopædia Britannica . Vol. 10 (11. Aufl.). S. 753–758.
- Weisstein, Eric W. „Fourier-Reihe“ . MathWorld .
- Joseph Fourier - Eine Seite über Fouriers Leben, die für den historischen Abschnitt dieses Artikels auf der Wayback Machine verwendet wurde (archiviert am 5. Dezember 2001)
Dieser Artikel enthält Material aus Beispielen der Fourier-Serie auf PlanetMath , die unter der Creative Commons Attribution/Share-Alike License lizenziert ist .

























![(-\pi ,\pi ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fbb1843079a9df3d3bbcce3249bb2599790de9c)



![{\displaystyle {\begin{aligned}A_{n}&={\frac {1}{\pi }}\int _{-\pi }^{\pi }s(x)\cos(nx)\, dx=0,\quad n\geq 0.\\[4pt]B_{n}&={\frac {1}{\pi }}\int _{-\pi }^{\pi }s(x) \sin(nx)\,dx\\[4pt]&=-{\frac {2}{\pi n}}\cos(n\pi )+{\frac {2}{\pi ^{2}n ^{2}}}\sin(n\pi )\\[4pt]&={\frac {2\,(-1)^{n+1}}{\pi n}},\quad n\geq 1.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/60820ad01df637675beb2c56a9db388cd0539490)

![{\displaystyle {\begin{aligned}s(x)&=A_{0}+\sum _{n=1}^{\infty }A_{n}\cos \left(nx\right)+B_{n }\sin \left(nx\right)\\[4pt]&={\frac {2}{\pi }}\sum _{n=1}^{\infty }{\frac {(-1)^ {n+1}}{n}}\sin(nx),\quad \mathrm {for} \quad x-\pi \notin 2\pi \mathbb {Z} .\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5cb0668def0fb376e8a1d8541263b10508260a77)
















![{\displaystyle [x_{0},x_{0}+P],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/74358f52e616039efc9b1fcc9568f99f6ae93463)
![{\displaystyle \mathrm {X} _{f}(\tau )={\tfrac {2}{P}}\int _{P}s(x)\cdot \cos \left(2\pi f(x -\tau )\right)\,dx;\quad \tau \in \left[0,{\tfrac {2\pi }{f}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2868da53c5e3ed8528137f2aaf139400251e74e)













![{\displaystyle {\begin{aligned}\mathrm {X} _{n}(\varphi )&={\tfrac {2}{P}}\int _{P}s(x)\cdot \cos \left (2\pi {\tfrac {n}{P}}x-\varphi \right)\,dx;\quad \varphi \in [0,2\pi ]\\&=\cos(\varphi )\cdot \underbrace {{\tfrac {2}{P}}\int _{P}s(x)\cdot \cos \left(2\pi {\tfrac {n}{P}}x\right)\,dx } _{A_{n}}+\sin(\varphi )\cdot \underbrace {{\tfrac {2}{P}}\int _{P}s(x)\cdot \sin \left(2\pi {\tfrac {n}{P}}x\right)\,dx}_{B_{n}}\\&=\cos(\varphi)\cdot A_{n}+\sin(\varphi)\cdot B_{n}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b72e0b83fd20619ddc5f938cf5280cfd3443820)








![{\displaystyle [x_{0},x_{0}+P]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ef79a1b836ec65eacb0d2c73464996d2b7830ba)






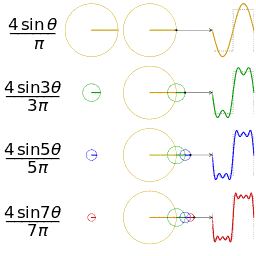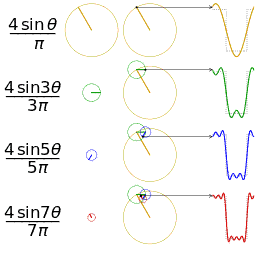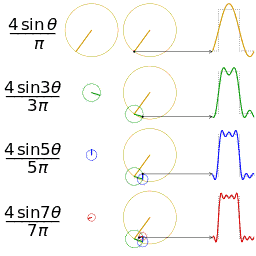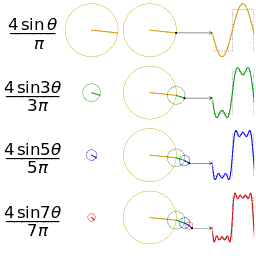


![{\displaystyle {\hat {s}}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4759449679108f08a78be5a080c3db89dc27ffea)
![{\displaystyle S[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b4222b53917b43f530116997b71049100c95586)
![{\displaystyle {\begin{aligned}s(x)&=\sum _{n=-\infty }^{\infty }{\hat {s}}(n)\cdot e^{2\pi inx/ P}&&{\text{übliche mathematische Notation}}\\&=\sum _{n=-\infty }^{\infty }S[n]\cdot e^{i\,2\pi nx/P} &&{\text{allgemeine technische Schreibweise}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e8427f6c9d293e4fd06f52432445973be52c41e)
![{\displaystyle S(f)\ \triangleq \ \sum _{n=-\infty }^{\infty }S[n]\cdot \delta \left(f-{\frac {n}{P}}\ Rechts),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6a4127cd2d8d239076aad35e6b82248554b6036)


![{\displaystyle {\begin{aligned}{\mathcal {F}}^{-1}\{S(f)\}&=\int _{-\infty }^{\infty }\left(\sum _ {n=-\infty }^{\infty }S[n]\cdot \delta \left(f-{\frac {n}{P}}\right)\right)e^{i2\pi fx}\ ,df,\\[6pt]&=\sum _{n=-\infty }^{\infty }S[n]\cdot \int _{-\infty }^{\infty }\delta \left(f -{\frac {n}{P}}\right)e^{i2\pi fx}\,df,\\[6pt]&=\sum _{n=-\infty }^{\infty }S[ n]\cdot e^{i\,2\pi nx/P}\ \ \triangleq \ s_{\infty }(x).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/446316db0d563e8ceac0da5d5d078b67f0c0f4e5)










![{\displaystyle (x,y)\in [0,\pi ]\times [0,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c18734f151b17b5d3e325f79c7000826ab832610)



















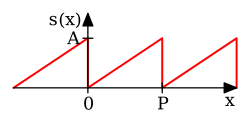








![{\displaystyle x\in [0,P].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06b058e43f16179590921d9669ac45cec21a975e)
![{\displaystyle S[n],R[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/320b593144d771f4aac1aae12d9513debbd3b20f)


![{\displaystyle a\cdot S[n]+b\cdot R[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/23622be4a50d54928d05c273e803240a2cb1e413)


![{\displaystyle S[-n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab628b28c49c04cab81d0bd30d19ee0797b0587c)

![{\displaystyle S^{*}[-n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a3f6ea8a947b86f8a31046070359f6b8111a0bae)

![{\displaystyle S^{*}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3776c67c40997d8044720ef84de7575679cf9638)

![{\displaystyle {\frac {1}{2}}(S[n]+S^{*}[-n])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2eb44dffaae6c85870914249c054e33236b02cc8)

![{\displaystyle {\frac {1}{2i}}(S[n]-S^{*}[-n])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc039a9c12ae20a4b47337ae55bf8a7bc26d2e11)

![{\displaystyle \operatorname {Re} {(S[n])}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/140ebff319eb8eb7965d0ca86dcaadb21685177a)

![{\displaystyle \operatorname {Im} {(S[n])}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c726948120015ce0d482f5f7f4af81713342b5c)

![{\displaystyle S[n]\cdot e^{-i{\frac {2\pi x_{0}}{P}}n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2fb7150e991a2642dc0c62cdee40602d99227420)


![{\displaystyle S[n-n_{0}]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07385c0e5fd45d4e07a279a91668cf8894963e0c)



![{\textstyle \lim _{|n|\to \infty }S[n]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fc04d857f6462ae29422edcada981c8a798d4b5)



![{\textstyle {\frac {1}{P}}\int _{P}|s(x)|^{2}\,dx=\sum _{n=-\infty }^{\infty }{\ Bigl |}S[n]{\Bigr |}^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/263e69a5a58598591a5c06ca7e17ef8cfe92bdad)


![{\displaystyle S[n]\in \mathbb {C} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/f5ef3e51d1a6c9fe833f0a436ad2906cfaa4d5a3)
![{\displaystyle {\frac {1}{P}}\int _{P}|s(x)|^{4}\,dx=\sum _{k=0}^{M-1}S[k ]\sum _{l=0}^{M-1}S^{*}[l]{\Bigg [}{\underset {k\geq l}{\sum _{m=kl}^{M- 1}}}S^{*}[m]S[m-(kl)]+{\underset {k<l}{\sum _{m=lk}^{M-1}}}S^{* }[m-(lk)]S[m]{\Bigg ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/39c359b6c8df5068b8df3c592e303ee7be010e33)
![{\displaystyle S[n]\in \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b094e88b3fbb3d7754e0a9ea0138c296f4b0d137)
![{\displaystyle {\frac {1}{P}}\int _{P}|s(x)|^{4}\,dx=\sum _{k=0}^{M-1}S[k ]\sum _{l=0}^{M-1}S[l]\sum _{m=|kl|}^{M-1}S[m]S[m-|kl|]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9aa31cd2ec580a3b95affae1462abed113a86f12)



![{\displaystyle S[n]=c_{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4375307afdf29e78a31ef64b699dcb3e2fde140)


![{\displaystyle R[n],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/80d8bbe147f3eb3fb318d09437a3540e054b0289)



![{\displaystyle H[n]=\{S*R\}[n].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b5d3978629d1c2cd954f884509a1bb360f01cac5)

![{\displaystyle H[n]=P\cdot S[n]\cdot R[n].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1804f502413d4e3e5f28f8715c52e2a3d7e7e9a6)


![{\displaystyle L^{1}([0,2\pi])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd16426bda528c05e32e97bfba7f51b598c081b8)





![{\displaystyle {\widehat {s'}}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a50845d25c79fe9547d0194fce67a390efc1a4ed)

![{\displaystyle {\widehat {s}}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/efb5adbeb52d198894dc8f70ec8c434f0e193e6b)
![{\displaystyle {\widehat {s'}}[n]=in{\widehat {s}}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d281471757291b705a757faa55af0f1cebf8a0b6)

![{\displaystyle {\widehat {s^{(k)}}}[n]=(in)^{k}{\widehat {s}}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b0120eafbcb1c02b4c2f81f5589fdc328c28bd20)

![{\displaystyle {\widehat {s^{(k)}}}[n]\bis 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ddeff4d322091a8ec85a30a10d584d426d703b1)

![{\displaystyle |n|^{k}{\widehat {s}}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/541244c281f9472e99fca9b32f2cd7676434d09c)


![[-\pi ,\pi ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb064fd6c55820cfa660eabeeda0f6e3c4935ae6)




![{\displaystyle [-\pi ,\pi ]\times [-\pi ,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df436805f50de7386abdb2a9d058672ec1b4cebb)
![{\displaystyle {\begin{aligned}f(x,y)&=\sum _{j,k\in \mathbb {Z} }c_{j,k}e^{ijx}e^{iky},\ \[5pt]c_{j,k}&={\frac {1}{4\pi ^{2}}}\int _{-\pi }^{\pi }\int _{-\pi }^ {\pi }f(x,y)e^{-ijx}e^{-iky}\,dx\,dy.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aec3723d7051701ab4530dce39f1480cef835981)



















![{\displaystyle \left[0,a_{1}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/187cf2c27876a96c668f73266f673002808773ac)



![{\displaystyle {\begin{aligned}h^{\mathrm {two} }(m_{1},m_{2},x_{3})&\triangleq {\frac {1}{a_{2}}} \int _{0}^{a_{2}}h^{\mathrm{eins} }(m_{1},x_{2},x_{3})\cdot e^{-i2\pi {\frac {m_{2}}{a_{2}}}x_{2}}\,dx_{2}\\[12pt]&={\frac {1}{a_{2}}}\int _{0} ^{a_{2}}dx_{2}{\frac {1}{a_{1}}}\int _{0}^{a_{1}}dx_{1}g(x_{1},x_{ 2},x_{3})\cdot e^{-i2\pi \left({\frac {m_{1}}{a_{1}}}x_{1}+{\frac {m_{2}} {a_{2}}}x_{2}\right)}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/342f2441863562e2188c632ea98d105ddb4ce5f1)

![{\displaystyle {\begin{aligned}h^{\mathrm {drei} }(m_{1},m_{2},m_{3})&\triangleq {\frac {1}{a_{3}}} \int _{0}^{a_{3}}h^{\mathrm{zwei} }(m_{1},m_{2},x_{3})\cdot e^{-i2\pi {\frac {m_{3}}{a_{3}}}x_{3}}\,dx_{3}\\[12pt]&={\frac {1}{a_{3}}}\int _{0} ^{a_{3}}dx_{3}{\frac {1}{a_{2}}}\int _{0}^{a_{2}}dx_{2}{\frac {1}{a_{ 1}}}\int _{0}^{a_{1}}dx_{1}g(x_{1},x_{2},x_{3})\cdot e^{-i2\pi \left( {\frac {m_{1}}{a_{1}}}x_{1}+{\frac {m_{2}}{a_{2}}}x_{2}+{\frac {m_{3} }{a_{3}}}x_{3}\right)}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a8c3fac5e04d1272c87fd58d3217a691214d09b)



















![{\displaystyle {\begin{vmatrix}{\dfrac {\partial x_{1}}{\partial x}}&{\dfrac {\partial x_{1}}{\partial y}}&{\dfrac {\ partiell x_{1}}{\partial z}}\\[12pt]{\dfrac {\partial x_{2}}{\partial x}}&{\dfrac {\partial x_{2}}{\partial y }}&{\dfrac {\partial x_{2}}{\partial z}}\\[12pt]{\dfrac {\partial x_{3}}{\partial x}}&{\dfrac {\partial x_ {3}}{\partial y}}&{\dfrac {\partial x_{3}}{\partial z}}\end{vmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e5df9134486606d6a55c8ec4a96ee3ca353e924)












![{\displaystyle L^{2}([-\pi ,\pi ])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f84fea7a212acaf14649b6cdcca282b0646a8b0)












![{\displaystyle s_{_{N}}(x)=\sum _{n=-N}^{N}S[n]\ e^{i{\tfrac {2\pi }{P}}nx} ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b030eaf773387de3787b4a003ef7599624be959)
![{\displaystyle p_{_{N}}(x)=\sum _{n=-N}^{N}p[n]\ e^{i{\tfrac {2\pi }{P}}nx} .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a29c02020f3c186b790b680deabe8e985ebcd700)







![{\displaystyle (i\cdot n)S[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a89ae55b94c8d25d1f3927c5ba4eb65ac7c4762)

![{\displaystyle n^{2}S[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/340e0b24995005f3669a865a57edb4035b77ca2d)


![{\displaystyle \sup _{x}|s(x)-s_{_{N}}(x)|\leq \sum _{|n|>N}|S[n]|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8225d322a5b676b2b1709c2a636dcd092ff11ec)
