Histogramm - Histogram

Histogramm
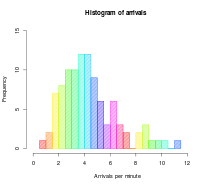Eines der sieben grundlegenden Qualitätswerkzeuge
Zuerst beschrieben von	Karl Pearson
Zweck	Grobbewertung der Wahrscheinlichkeitsverteilung einer gegebenen Variablen durch Darstellung der Häufigkeiten von Beobachtungen in bestimmten Wertebereichen.

Ein Histogramm ist eine ungefähre Darstellung der Verteilung numerischer Daten. Es wurde zuerst von Karl Pearson eingeführt . Um ein Histogramm zu konstruieren, besteht der erste Schritt darin, den Wertebereich zu " bin " (oder " bucket "), dh den gesamten Wertebereich in eine Reihe von Intervallen zu unterteilen, und dann zu zählen, wie viele Werte in jedes Intervall fallen. Die Bins werden normalerweise als aufeinanderfolgende, sich nicht überschneidende Intervalle einer Variablen angegeben. Die Bins (Intervalle) müssen benachbart sein und sind oft (aber nicht erforderlich) gleich groß.

Wenn die Bins gleich groß sind, wird über dem Bin ein Rechteck errichtet, dessen Höhe proportional zur Häufigkeit – der Anzahl der Fälle in jedem Bin – ist. Ein Histogramm kann auch normalisiert werden , um "relative" Häufigkeiten anzuzeigen. Es zeigt dann den Anteil der Fälle, die in jede von mehreren Kategorien fallen , wobei die Summe der Höhen gleich 1 ist.

Fächer müssen jedoch nicht die gleiche Breite aufweisen; in diesem Fall ist die Fläche des aufgerichteten Rechtecks proportional zur Häufigkeit der Fälle in dem Behälter. Die vertikale Achse ist dann nicht die Häufigkeit, sondern die Häufigkeitsdichte – die Anzahl der Fälle pro Einheit der Variablen auf der horizontalen Achse. Beispiele für variable Fachbreiten werden unten in den Daten des Volkszählungsbüros angezeigt.

Da die benachbarten Bins keine Lücken hinterlassen, berühren sich die Rechtecke eines Histogramms, um anzuzeigen, dass die ursprüngliche Variable kontinuierlich ist.

Histogramme geben einen groben Eindruck von der Dichte der zugrunde liegenden Verteilung der Daten und häufig zur Dichteschätzung : Schätzen der Wahrscheinlichkeitsdichtefunktion der zugrunde liegenden Variablen. Die Gesamtfläche eines Histogramms, das für die Wahrscheinlichkeitsdichte verwendet wird, wird immer auf 1 normiert. Wenn die Länge der Intervalle auf der x- Achse alle 1 beträgt, ist ein Histogramm identisch mit einem relativen Häufigkeitsdiagramm .

Ein Histogramm kann man sich als vereinfachte Kerneldichteschätzung vorstellen , die einen Kernel verwendet , um Frequenzen über die Bins zu glätten. Dies ergibt eine glattere Wahrscheinlichkeitsdichtefunktion, die im Allgemeinen die Verteilung der zugrunde liegenden Variablen genauer widerspiegelt. Die Dichteschätzung könnte als Alternative zum Histogramm geplottet werden und wird normalerweise als Kurve und nicht als Satz von Kästchen gezeichnet. Dennoch werden Histogramme in Anwendungen bevorzugt, wenn ihre statistischen Eigenschaften modelliert werden müssen. Die korrelierte Variation einer Kerneldichteschätzung ist mathematisch sehr schwer zu beschreiben, während sie für ein Histogramm einfach ist, bei dem jeder Bin unabhängig variiert.

Eine Alternative zur Schätzung der Kerneldichte ist das durchschnittlich verschobene Histogramm, das schnell zu berechnen ist und eine glatte Kurvenschätzung der Dichte ohne Verwendung von Kernen liefert.

Das Histogramm ist eines der sieben grundlegenden Werkzeuge der Qualitätskontrolle .

Histogramme werden manchmal mit Balkendiagrammen verwechselt. Ein Histogramm wird für kontinuierliche Daten verwendet , wobei die Klassen Datenbereiche darstellen, während ein Balkendiagramm ein Diagramm kategorialer Variablen ist . Einige Autoren empfehlen, dass Balkendiagramme Lücken zwischen den Rechtecken aufweisen, um die Unterscheidung zu verdeutlichen.

Beispiele

Dies sind die Daten für das Histogramm rechts mit 500 Elementen:

Die zur Beschreibung der Muster in einem Histogramm verwendeten Wörter sind: "symmetrisch", "linksschief" oder "rechts", "unimodal", "bimodal" oder "multimodal".

• 

  Symmetrisch, unimodal

• 

  Rechts verdreht

• 

  Links verdreht

• 

  Bimodal

• 

  Multimodal

• 

  Symmetrisch

Es ist eine gute Idee, die Daten mit mehreren verschiedenen Bin-Breiten darzustellen, um mehr darüber zu erfahren. Hier ist ein Beispiel für Trinkgelder, die in einem Restaurant gegeben werden.

• 

  Tipps mit einer Bin-Breite von 1 $, nach rechts geneigt, unimodal

• 

  Tipps mit einer Bin-Breite von 10c, immer noch rechtsschief, multimodal mit Modi bei $- und 50c-Beträgen, weist auf Rundungen hin, auch einige Ausreißer

Das US Census Bureau stellte fest, dass 124 Millionen Menschen außer Haus arbeiten. Die folgende Tabelle zeigt anhand ihrer Angaben zur Fahrtzeit zur Arbeit, dass die absolute Zahl der Personen, die mit Fahrtzeiten „mindestens 30, aber weniger als 35 Minuten“ geantwortet haben, höher ist als die Zahlen für die Kategorien darüber und darunter. Dies ist wahrscheinlich darauf zurückzuführen, dass Personen ihre angegebene Reisezeit runden. Das Problem der Angabe von Werten als etwas willkürlich gerundete Zahlen ist ein häufiges Phänomen beim Sammeln von Daten von Personen.

Histogramm der Reisezeit (zur Arbeit), US-Volkszählung 2000. Die Fläche unter der Kurve entspricht der Gesamtzahl der Fälle. Dieses Diagramm verwendet Q/Breite aus der Tabelle.

Daten nach absoluten Zahlen

Intervall	Breite	Menge	Menge/Breite
0	5	4180	836
5	5	13687	2737
10	5	18618	3723
fünfzehn	5	19634	3926
20	5	17981	3596
25	5	7190	1438
30	5	16369	3273
35	5	3212	642
40	5	4122	824
45	fünfzehn	9200	613
60	30	6461	215
90	60	3435	57

Dieses Histogramm zeigt die Anzahl der Fälle pro Einheitsintervall als Höhe jedes Blocks, sodass die Fläche jedes Blocks gleich der Anzahl der Personen in der Umfrage ist, die in seine Kategorie fallen. Die Fläche unter der Kurve repräsentiert die Gesamtzahl der Fälle (124 Millionen). Diese Art von Histogramm zeigt absolute Zahlen mit Q in Tausend.

Histogramm der Reisezeit (zur Arbeit), US-Volkszählung 2000. Fläche unter der Kurve gleich 1. Dieses Diagramm verwendet Q/Gesamt/Breite aus der Tabelle.

Daten nach Anteilen

Intervall	Breite	Menge (Q)	Q/Gesamt/Breite
0	5	4180	0,0067
5	5	13687	0,0221
10	5	18618	0,0300
fünfzehn	5	19634	0,0316
20	5	17981	0,0290
25	5	7190	0,0116
30	5	16369	0,0264
35	5	3212	0,0052
40	5	4122	0,0066
45	fünfzehn	9200	0,0049
60	30	6461	0,0017
90	60	3435	0,0005

Dieses Histogramm unterscheidet sich vom ersten nur in der vertikalen Skala. Die Fläche jedes Blocks ist der Bruchteil der Gesamtheit, die jede Kategorie darstellt, und die Gesamtfläche aller Balken ist gleich 1 (der Bruch bedeutet "alle"). Die angezeigte Kurve ist eine einfache Dichteschätzung . Diese Version zeigt Proportionen und wird auch als Flächenhistogramm bezeichnet.

Mit anderen Worten stellt ein Histogramm eine Häufigkeitsverteilung durch Rechtecke dar, deren Breiten Klassenintervalle darstellen und deren Flächen proportional zu den entsprechenden Häufigkeiten sind: deren Höhe ist jeweils die durchschnittliche Häufigkeitsdichte für das Intervall. Die Intervalle werden zusammengefügt, um zu zeigen, dass die durch das Histogramm dargestellten Daten zwar ausschließlich, aber auch zusammenhängend sind. (Zum Beispiel ist es in einem Histogramm möglich, zwei Verbindungsintervalle von 10,5–20,5 und 20,5–33,5 zu haben, aber nicht zwei Verbindungsintervalle von 10,5–20,5 und 22,5–32,5. Leere Intervalle werden als leer dargestellt und nicht übersprungen.)

Mathematische Definitionen

Ein gewöhnliches und ein kumulatives Histogramm derselben Daten. Die gezeigten Daten sind eine Zufallsstichprobe von 10.000 Punkten aus einer Normalverteilung mit einem Mittelwert von 0 und einer Standardabweichung von 1.

Die zur Konstruktion eines Histogramms verwendeten Daten werden über eine Funktion m _{i erzeugt} , die die Anzahl der Beobachtungen zählt, die in jede der disjunkten Kategorien (bekannt als Bins ) fallen. Wenn wir n die Gesamtzahl der Beobachtungen und k die Gesamtzahl der Bins seien, erfüllen die Histogrammdaten m _i die folgenden Bedingungen:

${\displaystyle n=\sum_{i=1}^{k}{m_{i}}.}$

Kumulatives Histogramm

Ein kumulatives Histogramm ist ein Mapping, das die kumulative Anzahl von Beobachtungen in allen Bins bis zum angegebenen Bin zählt. Das heißt, das kumulative Histogramm M _i eines Histogramms m _j ist definiert als:

${\displaystyle M_{i}=\sum_{j=1}^{i}{m_{j}}.}$

Anzahl der Behälter und Breite

Es gibt keine "beste" Anzahl von Bins, und unterschiedliche Bin-Größen können unterschiedliche Merkmale der Daten offenbaren. Datengruppierung ist so alt wie mindestens Graunt ‚Werk im 17. Jahrhundert, aber keine systematischen Richtlinien wurden bis gegeben Sturges ‘ Arbeit im Jahr 1926.

Die Verwendung breiterer Bins, bei denen die Dichte der zugrunde liegenden Datenpunkte gering ist, reduziert das Rauschen aufgrund der Stichprobenzufälligkeit; Die Verwendung schmalerer Bins bei hoher Dichte (so dass das Signal das Rauschen übertönt) verleiht der Dichteschätzung eine höhere Präzision. Somit kann das Variieren der Bin-Breite innerhalb eines Histogramms von Vorteil sein. Nichtsdestotrotz werden Behälter gleicher Breite weit verbreitet verwendet.

Einige Theoretiker haben versucht, eine optimale Anzahl von Bins zu bestimmen, aber diese Verfahren machen im Allgemeinen starke Annahmen über die Form der Verteilung. Abhängig von der tatsächlichen Datenverteilung und den Zielen der Analyse können unterschiedliche Bin-Breiten geeignet sein, sodass normalerweise Experimente erforderlich sind, um eine geeignete Breite zu bestimmen. Es gibt jedoch verschiedene nützliche Richtlinien und Faustregeln.

Die Anzahl der Bins k kann direkt zugewiesen oder aus einer vorgeschlagenen Bin-Breite h berechnet werden  als:

${\displaystyle k=\left\lceil {\frac {\max x-\min x}{h}}\right\rceil .}$

Die Klammern zeigen die Deckenfunktion an .

Quadratwurzel-Wahl

${\displaystyle k=\lceil {\sqrt {n}}\rceil\,}$

die die Quadratwurzel der Anzahl der Datenpunkte in der Stichprobe nimmt (von Excel-Histogrammen und vielen anderen verwendet) und auf die nächste ganze Zahl rundet .

Sturges' Formel

Die Sturges-Formel ist aus einer Binomialverteilung abgeleitet und nimmt implizit eine annähernd normale Verteilung an.

${\displaystyle k=\lceil\log_{2}n\rceil +1,\,}$

Die Formel von Sturges basiert implizit auf dem Bereich der Daten und kann schlecht funktionieren, wenn n  < 30 , da die Anzahl der Klassen klein ist – weniger als sieben – und es unwahrscheinlich ist, dass Trends in den Daten gut dargestellt werden. Auf der anderen Seite kann die Formel von Sturges die Bin-Breite für sehr große Datensätze überschätzen, was zu übermäßig geglätteten Histogrammen führt. Es kann auch eine schlechte Leistung erbringen, wenn die Daten nicht normalverteilt sind.

Im Vergleich mit der Scott-Regel und der Terrell-Scott-Regel, zwei anderen weithin akzeptierten Formeln für Histogramm-Bins, ist die Ausgabe der Sturges-Formel am nächsten, wenn n 100 ist .

Reisregel

${\displaystyle k=\lceil 2{\sqrt[{3}]{n}}\rceil,}$

Die Reisregel wird als einfache Alternative zur Sturges-Regel vorgestellt.

Doanes Formel

Die Formel von Doane ist eine Modifikation der Formel von Sturges, die versucht, ihre Leistung mit nicht normalen Daten zu verbessern.

${\displaystyle k=1+\log_{2}(n)+\log_{2}\left(1+{\frac {|g_{1}|}{\sigma_{g_{1}}} }\rechts)}$

wo ist die geschätzte 3.-Moment- Schiefe der Verteilung und ${\displaystyle g_{1}}$

${\displaystyle \sigma_{g_{1}}={\sqrt {\frac {6(n-2)}{(n+1)(n+3)}}}}$

Scotts normale Referenzregel

Die Behälterbreite ist gegeben durch ${\displaystyle h}$

${\displaystyle h={\frac {3.49{\hat {\sigma}}}{\sqrt[{3}]{n}}},}$

wo ist die Standardabweichung der Stichprobe . Die Normalreferenzregel von Scott ist optimal für zufällige Stichproben normalverteilter Daten, da sie den integrierten mittleren quadratischen Fehler der Dichteschätzung minimiert. ${\displaystyle {\hat {\sigma}}}$

Freedman-Diaconis' Wahl

Die Freedman-Diaconis-Regel gibt die Bin-Breite als: ${\displaystyle h}$

${\displaystyle h=2{\frac {\operatorname {IQR} (x)}{\sqrt[{3}]{n}}},}$

die auf dem Interquartilsabstand basiert , der mit IQR bezeichnet wird. Es ersetzt 3,5σ der Scott-Regel durch 2 IQR, das weniger empfindlich ist als die Standardabweichung gegenüber Ausreißern in den Daten.

Minimierung des geschätzten quadratischen Fehlers der Kreuzvalidierung

Dieser Ansatz zur Minimierung des integrierten mittleren quadratischen Fehlers aus der Scott-Regel kann über Normalverteilungen hinaus verallgemeinert werden, indem man eine Kreuzvalidierung auslässt:

${\displaystyle {\underset {h}{\operatorname {arg\,min} }}{\hat {J}}(h)={\underset {h}{\operatorname {arg\,min} }}\left ({\frac {2}{(n-1)h}}-{\frac {n+1}{n^{2}(n-1)h}}\sum _{k}N_{k}^ {2}\rechts)}$

Hier ist die Anzahl von Datenpunkten im k- ten Bin, und die Wahl des Wertes von h , der J minimiert , minimiert den integrierten mittleren quadratischen Fehler. ${\displaystyle N_{k}}$

Shimazaki und Shinomotos Wahl

Die Wahl basiert auf der Minimierung einer geschätzten L ² -Risikofunktion

${\displaystyle {\underset {h}{\operatorname {arg\,min}}}{\frac {2{\bar {m}}-v}{h^{2}}}}$

wobei und die mittlere und verzerrte Varianz eines Histogramms mit bin-width sind , und . ${\displaystyle \textstyle {\bar {m}}}$${\displaystyle \textstyle v}$${\displaystyle \textstyle h}$${\displaystyle \textstyle {\bar{m}}={\frac {1}{k}}\sum _{i=1}^{k}m_{i}}$${\displaystyle \textstyle v={\frac {1}{k}}\sum _{i=1}^{k}(m_{i}-{\bar {m}})^{2}}$

Variable Behälterbreiten

Anstatt gleich beabstandete Behälter zu wählen, ist es für einige Anwendungen vorzuziehen, die Behälterbreite zu variieren. Dies vermeidet Behälter mit niedrigen Zählungen. Ein häufiger Fall besteht darin, gleichwahrscheinliche Behälter zu wählen , bei denen erwartet wird, dass die Anzahl der Abtastwerte in jedem Behälter ungefähr gleich ist. Die Bins können gemäß einer bekannten Verteilung ausgewählt werden oder können basierend auf den Daten ausgewählt werden, so dass jede Bin Samples hat. Beim Plotten des Histogramms wird die Häufigkeitsdichte für die abhängige Achse verwendet. Während alle Bins ungefähr die gleiche Fläche haben, nähern sich die Höhen des Histogramms der Dichteverteilung an. ${\displaystyle \approx n/k}$

Für gleichwahrscheinliche Behälter wird folgende Regel für die Anzahl der Behälter vorgeschlagen:

${\displaystyle k=2n^{2/5}}$

Diese Auswahl von Bins wird durch die Maximierung der Leistung eines Pearson-Chi-Quadrat-Tests motiviert, der prüft, ob die Bins die gleiche Anzahl von Abtastwerten enthalten. Genauer gesagt wird empfohlen , für ein gegebenes Konfidenzintervall zwischen dem 1/2- und dem 1-fachen der folgenden Gleichung zu wählen: ${\displaystyle\alpha}$

${\displaystyle k=4\left({\frac {2n^{2}}{\Phi^{-1}(\alpha)}}\right)^{\frac {1}{5}}}$

Wo ist die Probitfunktion . Folgt man dieser Regel für würde zwischen und geben ; der Koeffizient 2 wird als leicht zu merkender Wert aus diesem breiten Optimum gewählt. ${\displaystyle \Phi^{-1}}$${\displaystyle \alpha =0.05}$${\displaystyle 1.88n^{2/5}}$${\displaystyle 3.77n^{2/5}}$

Anmerkung

Ein guter Grund, warum die Anzahl der Bins proportional sein sollte, ist folgender: Angenommen, die Daten werden als unabhängige Realisierungen einer beschränkten Wahrscheinlichkeitsverteilung mit glatter Dichte erhalten. Dann bleibt das Histogramm ebenso "robust" wie es ins Unendliche tendiert. Wenn die "Breite" der Verteilung ist (z. B. die Standardabweichung oder der Interquartilbereich), dann ist die Anzahl der Einheiten in einem Bin (die Häufigkeit) von Ordnung und der relative Standardfehler ist von Ordnung . Im Vergleich zum nächsten Bin ist die relative Änderung der Frequenz von Ordnung, vorausgesetzt, die Ableitung der Dichte ist nicht Null. Diese beiden sind von der gleichen Ordnung, wenn es von Ordnung ist , also ist das von der Ordnung . Diese einfache Kubikwurzelwahl kann auch auf Behälter mit nicht konstanter Breite angewendet werden. ${\displaystyle {\sqrt[{3}]{n}}}$${\displaystyle n}$${\displaystyle n}$${\displaystyle s}$${\displaystyle nh/s}$${\displaystyle {\sqrt {s/(nh)}}}$${\displaystyle h/s}$${\displaystyle h}$${\displaystyle s/{\sqrt[{3}]{n}}}$${\displaystyle k}$${\displaystyle {\sqrt[{3}]{n}}}$

Histogramm und Dichtefunktion für eine Gumbel-Verteilung

Anwendungen

• In der Hydrologie werden das Histogramm und die geschätzte Dichtefunktion von Niederschlags- und Flussabflussdaten, die mit einer Wahrscheinlichkeitsverteilung analysiert werden, verwendet, um Einblick in ihr Verhalten und ihre Auftretenshäufigkeit zu gewinnen. Ein Beispiel ist in der blauen Abbildung dargestellt.
• In vielen digitalen Bildbearbeitungsprogrammen gibt es ein Histogramm-Tool, das Ihnen die Verteilung des Kontrasts / der Helligkeit der Pixel anzeigt .
  

  Histogramm des Kontrasts

Siehe auch

• Datenbinning
• Dichteschätzung
  • Kerneldichteschätzung , eine glattere, aber komplexere Methode zur Dichteschätzung
• Entropieschätzung
• Freedman-Diaconis-Regel
• Bildhistogramm
• Pareto-Diagramm
• Sieben grundlegende Qualitätswerkzeuge
• V-optimale Histogramme

Verweise

Weiterlesen

• Lancaster, HO Eine Einführung in die medizinische Statistik. John Wiley und Söhne. 1974. ISBN  0-471-51250-8

Externe Links

• Exploring Histograms , ein Essay von Aran Lunzer und Amelia McNamara
• Arbeitsweg und Arbeitsort (Standort des im Beispiel zitierten Volkszählungsdokuments)
• Glattes Histogramm für Signale und Bilder von wenigen Samples
• Histogramme: Konstruktion, Analyse und Verständnis mit externen Links und einer Anwendung auf die Teilchenphysik.
• Eine Methode zur Auswahl der Behältergröße eines Histogramms
• Histogramme: Theorie und Praxis , einige großartige Illustrationen einiger der oben abgeleiteten Konzepte der Bin-Breite.
• Histogramme richtig
• Interaktiver Histogrammgenerator
• Matlab-Funktion zum Zeichnen schöner Histogramme
• Dynamisches Histogramm in MS Excel
• Histogramm Konstruktion und Manipulation mit Hilfe von Java - Applets und Diagrammen auf SOCR
• Toolbox zum Erstellen der besten Histogramme