Katapayadi-System - Katapayadi system

Dieser Artikel enthält indischen Text . Ohne geeignete Rendering-Unterstützung werden möglicherweise Fragezeichen oder Kästchen , falsch platzierte Vokale oder fehlende Konjunkte anstelle von indischem Text angezeigt.

ka · ta · pa · yā · di ( Devanagari : कटपयादि) System (auch bekannt als Paralppēru , Malayalam: പരല്പ്പേര് ) der numerischen Notation ist ein altes indisches alphasyllabic Zahlensystem zu zeigen Buchstaben auf Zahlen füreinfache Erinnerung an Zahlen als Worte oder Verse . Durch das Zuweisen von mehr als einem Buchstaben zu einer Zahl und das Annullieren bestimmter anderer Buchstaben als wertlos, bietet dieses System die Flexibilität, aus Zahlen, die sich leicht merken können, bedeutungsvolle Wörter zu bilden.

Geschichte

Der älteste verfügbare Beweis für die Verwendung des Kaṭapayādi-Systems (Sanskrit: कटपयादि) stammt aus Grahacāraṇibandhana von Haridatta im Jahr 683 n . Chr . . Es wurde in Laghu bhāskarīya vivaraṇa verwendet, das 869 n . Chr . von Śaṅkara.nārāyaṇa geschrieben wurde .

Einige argumentieren, dass das System von Vararuci stammt . In einigen astronomischen Texten, die in Kerala populär waren, wurden Planetenpositionen im Kaṭapayādi-System kodiert. Als erstes solches Werk gilt das Chandra-vakyani von Vararuci , das traditionell dem vierten Jahrhundert n . Chr . zugeordnet wird . Daher ist irgendwann im frühen ersten Jahrtausend eine vernünftige Schätzung für den Ursprung des Kaṭapayādi- Systems.

Es ist bekannt, dass Aryabhata in seiner Abhandlung Ārya·bhaṭīya ein ähnliches, komplexeres System verwendet hat, um astronomische Zahlen darzustellen . Es gibt keine definitiven Beweise dafür, ob das Ka-ṭa-pa-yā-di- System aus der Āryabhaṭa -Zählung stammt .

Geografische Verbreitung der Nutzung

Fast alle Beweise für die Verwendung des Ka-ṭa-pa-yā-di- Systems stammen aus Südindien , insbesondere aus Kerala . Über seine Verwendung in Nordindien ist nicht viel bekannt. Auf einem in Nordindien entdeckten Sanskrit- Astrolab sind jedoch die Höhengrade im Kaṭapayādi- System markiert . Es wird in der Sarasvati Bhavan Bibliothek der Sampurnanand Sanskrit Universität in Varanasi aufbewahrt .

Das Ka-ṭa-pa-yā-di- System ist nicht auf Indien beschränkt. In Burma wurden einige Pali- Chronogramme entdeckt, die auf dem Ka-ṭa-pa-yā-di- System basieren .

Regeln und Praktiken

Der folgende Vers aus Śaṅkaravarmans Sadratnamāla erklärt den Mechanismus des Systems.

नञावचश्च शून्यानि संख्या: कटपयादय:।
मिश्रे तूपान्त्यहल् संख्या न च चिन्त्यो हलस्वर:॥

Transiliteration:

nanyāvacaśca śūnyāni saṃkhyāḥ kaṭapayādayaḥ
miśre tūpāntyahal saṃkhyā na ca cintyo halasvaraḥ

Übersetzung: na (न), nya (ञ) und a (अ)-s, dh Vokale repräsentieren Null . Die neun ganzen Zahlen werden durch Konsonantengruppen dargestellt , die mit ka , ṭa , pa , ya beginnen . Bei einem konjunktiven Konsonanten zählt nur der letzte der Konsonanten. Ein Konsonant ohne Vokal ist zu ignorieren.

Erläuterung: Die Zuordnung der Buchstaben zu den Ziffern erfolgt nach folgender Anordnung (in Devanagari, Kannada, Telugu & Malayalam)

1	2	3	4	5	6	7	8	9	0
ka क ಕ క ക	kha ख ಖ ఖ ഖ	ga ग ಗ గ ഗ	gha घ ಘ ఘ ഘ	nga ङ ಙ జ్ఞ ങ	ca च ಚ చ ച	cha छ ಛ ఛ ഛ	ja ज ಜ జ ജ	jha झ ಝ ఝ ഝ	nya ञ ಞ ఞ ഞ
ṭa ट ಟ ట ട	ṭha ठ ಠ ఠ ഠ	ḍa ड ಡ డ ഡ	ḍha ढ ಢ ఢ ഢ	ṇa ण ಣ ణ ണ	ta त ತ త ത	tha थ ಥ థ ഥ	da द ದ ద ദ	dha ध ಧ ధ ധ	na न ನ న ന
pa प ಪ ప പ	pha फ ಫ ఫ ഫ	ba ब బ ബ	bha भ ಭ భ ഭ	ma म ಮ మ മ	–	–	–	–	–
ya य ಯ య യ	ra र ರ ర ര	la ल ల ల ല	va व ವ వ വ	śha श ಶ శ ശ	sha ष ಷ ష ഷ	sa स ಸ స സ	ha ह ಹ హ ഹ	–	–

• Konsonanten haben Ziffern, die gemäß der obigen Tabelle zugewiesen werden. Zum Beispiel ist ba (ब) immer 3, während 5 entweder durch nga (ङ) oder ṇa (ण) oder ma (म) oder śha (श) dargestellt werden kann.
• Alle eigenständigen Vokale wie a (अ) und ṛ (ऋ) werden Null zugewiesen.
• Im Falle einer Konjunktion sind Konsonanten, die an einen Nichtvokal angehängt sind, wertlos. Zum Beispiel wird kya (क्या) gebildet durch k (क्) + ya (य) + a (अ). Der einzige Konsonant, der mit einem Vokal steht, ist ya (य). Die entsprechende Zahl für kya (क्या) ist also 1.
• Es gibt keine Möglichkeit, das Dezimaltrennzeichen im System darzustellen.
• Die Inder verwendeten das hindu-arabische Zahlensystem zur Nummerierung, das traditionell in aufsteigenden Stellenwerten von links nach rechts geschrieben wurde. Dies entspricht der Regel "अङ्कानां वामतो गतिः", was bedeutet, dass die Zahlen von rechts nach links gehen.

Variationen

• Der Konsonant ( Malayālam : ള, Devanāgarī : ळ, Kannada : ಳ) wird in Werken verwendet, die das Kaṭapayādi-System verwenden, wie die Sinustabelle von Mādhava .
• Praktiker des Spätmittelalters bilden die eigenständigen Vokale nicht auf Null ab. Aber manchmal wird es als wertlos angesehen.

Verwendungszweck

Mathematik und Astronomie

• Mādhava der Sinus - Tabelle aufgebaut durch 14. Jahrhundert Kerala Mathematiker - Astronom mādhava von Sangama · Grama beschäftigt das Kaṭapayādi System die trigonometrischen Sinus- von Winkeln zu gewinnen.
• Karaṇa·paddhati , geschrieben im 15. Jahrhundert, hat den folgenden śloka für den Wert von pi (π)

അനൂനനൂന്നാനനനുന്നനിത്യൈ-

സ്സമാഹതാശ്ചക്രകലാവിഭക്താഃ

ചണ്ഡാംശുചന്ദ്രാധമകുംഭിപാലൈർ-

വ്യാസസ്തദർദ്ധം ത്രിഭമൗർവിക സ്യാത്‌

Transliteration

anūnanūnnānananunnanityai

ssmāhatāścakra kalāvibhaktoḥ

caṇḍāṃśucandrādhamakuṃbhipālair

vyāsastadarddhaṃ tribhamaurvika syāt

Es gibt den Umfang eines Kreises mit Durchmesser anūnanūnnānananunnanityai (10.000.000.000) als caṇḍāṃśucandrādhamakuṃbhipālair (31415926536) an.

• aṅkara·varmans Sad·ratna·mālā verwendet das Kaṭapayādi-System. Der erste Vers von Kapitel 4 des Sad·ratna·mālā endet mit der Zeile:

(स्याद्) भद्राम्बुधिसिद्धजन्मगणितश्रद्धा स्म यद् भूपगी:

Transliteration

(syād) bhadrāmbudhisiddhajanmagaṇitaśraddhā sma yad bhūpagīḥ

Die Aufteilung der Konsonanten in die entsprechende Phrase ergibt,

भ bha	d	rā	m	bu	d	धि dhi	सि si	d	ध dha	ज ja	न् nein	ma	ga	णि ṇi	त ta	श् ś	ra	d	धा dhā	so	ma	ja	d	भू bhū	pa	गी gī
4	–	2	–	3	–	9	7	–	9	8	–	5	3	5	6	–	2	–	9	–	5	1	–	4	1	3

Wenn wir die Ziffern auf die heutige Verwendung in absteigender Reihenfolge der Dezimalstellen umkehren , erhalten wir 314159265358979324, was dem Wert von pi (π) auf 17 Dezimalstellen entspricht, außer dass die letzte Ziffer auf 4 gerundet werden könnte.

• Dieser Vers verschlüsselt den Wert von pi (π) bis zu 31 Dezimalstellen.

 गोपीभाग्यमधुव्रात-शृङ्गिशोदधिसन्धिग॥
 खलजीवितखाताव गलहालारसंधर॥

 ಗೋಪೀಭಾಗ್ಯಮಧುವ್ರಾತ-ಶೃಂಗಿಶೋದಧಿಸಂಧಿಗ ||
 ಖಲಜೀವಿತಖಾತಾವ ಗಲಹಾಲಾರಸಂಧರ ||

Dieser Vers ergibt direkt das dezimale Äquivalent von pi geteilt durch 10: pi/10 = 0,31415926535897932384626433832792

 గోపీభాగ్యమధువ్రాత-శృంగిశోదధిసంధిగ |
 ఖలజీవితఖాతావ గలహాలారసంధర ||

Traditionell wird die Reihenfolge der Ziffern im Katapayadi-System umgekehrt, um die Zahl zu bilden. Diese Regel wird in dieser Sloka verletzt.

Karnatische Musik

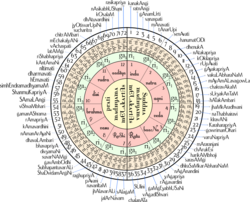
• Die melakarta ragas der karnatischen Musik werden so benannt, dass die ersten beiden Silben des Namens ihre Nummer ergeben. Dieses System wird manchmal Ka-ta-pa-ya-di sankhya genannt . Die Swaras 'Sa' und 'Pa' sind festgelegt, und hier ist, wie man die anderen Swaras von der Melakarta-Nummer erhält.

1. Melakartas 1 bis 36 haben Ma1 und die von 37 bis 72 haben Ma2.
2. Die anderen Noten werden durch Notieren des (ganzzahligen) Quotienten und des Restes abgeleitet, wenn einer kleiner als die Melakarta-Zahl durch 6 geteilt wird. Wenn die Melakarta-Zahl größer als 36 ist, subtrahiere 36 von der Melakarta-Zahl, bevor du diesen Schritt ausführst.
3. 'Ri'- und 'Ga'-Positionen: Der Raga hat:
   • Ri1 und Ga1 wenn der Quotient 0 . ist
   • Ri1 und Ga2, wenn der Quotient 1 . ist
   • Ri1 und Ga3, wenn der Quotient 2 . ist
   • Ri2 und Ga2, wenn der Quotient 3 . ist
   • Ri2 und Ga3, wenn der Quotient 4 . ist
   • Ri3 und Ga3, wenn der Quotient 5 . ist
4. 'Da'- und 'Ni'-Positionen: Der Raga hat:
   • Da1 und Ni1 wenn Rest 0 . ist
   • Da1 und Ni2, wenn Rest 1 . ist
   • Da1 und Ni3, wenn Rest 2 . ist
   • Da2 und Ni2, wenn Rest 3 . ist
   • Da2 und Ni3, wenn der Rest 4 . beträgt
   • Da3 und Ni3, wenn der Rest 5 . beträgt

• Siehe Swaras in Carnatic Music für Details zur obigen Notation.

Raga Dheerasankarabharanam

Das Katapayadi-Schema verbindet dha 9 und ra 2, daher ist die Melakarta-Zahl des Raga 29 (92 umgekehrt). Jetzt 29 36, daher hat Dheerasankarabharanam Ma1. Teilen Sie 28 (1 weniger als 29) durch 6, der Quotient ist 4 und der Rest 4. Daher hat dieser Raga Ri2, Ga3 (Quotient ist 4) und Da2, Ni3 (der Rest ist 4). Daher ist die Skala dieses Raga Sa Ri2 Ga3 Ma1 Pa Da2 Ni3 SA . ${\displaystyle \leftrightarrow}$${\displaystyle \leftrightarrow}$${\displaystyle \leq}$

Raga MechaKalyani

Aus dem Kodierungsschema Ma 5, Cha 6. Daher ist die Melakarta-Zahl des Raga 65 (56 umgekehrt). 65 ist größer als 36. MechaKalyani hat also Ma2. Da die Zahl des Raga größer als 36 ist, ziehen Sie 36 davon ab. 65–36=29. 28 (1 kleiner als 29) geteilt durch 6: Quotient=4, Rest=4. Ri2Ga3 tritt auf. Da2 Ni3 tritt auf. MechaKalyani hat also die Noten Sa Ri2 Ga3 Ma2 Pa Da2 Ni3 SA . ${\displaystyle \leftrightarrow}$${\displaystyle \leftrightarrow}$

Ausnahme für Simhendramadhyamam

Nach der obigen Berechnung sollten wir Sa 7, Ha 8 erhalten, was die Zahl 87 anstelle von 57 für Simhendramadhyamam ergibt. Dies sollte idealerweise Sa 7, Ma 5 mit der Zahl 57 sein. Daher wird angenommen, dass der Name als Sihmendramadhyamam geschrieben werden sollte (wie im Fall von Bra hm ana in Sanskrit). ${\displaystyle \leftrightarrow}$${\displaystyle \leftrightarrow}$${\displaystyle \leftrightarrow}$${\displaystyle \leftrightarrow}$

Darstellung von Terminen

Wichtige Daten wurden gespeichert , indem sie mit dem Kaṭapayādi- System konvertiert wurden. Diese Daten werden im Allgemeinen als Anzahl der Tage seit Beginn des Kali Yuga dargestellt . Es wird manchmal Kalidina Sankhya genannt .

• Der Malayalam - Kalender bekannt als kollavarsham (Malayalam: കൊല്ലവര്ഷം) wurde in Kerala angenommen von 825 beginnend CE , einige Kalender Modernisierungen. Dieses Datum wird als āchārya vāgbhadā in Erinnerung gerufen , umgewandelt mit Kaṭapayādi in 1434160 Tage seit Beginn des Kali Yuga .
• Narayaniyam , geschrieben von Melpathur Narayana Bhattathiri , endet mit der Zeile āyurārogyasaukhyam (ആയുരാരോഗ്യസൌഖ്യം), die langes Leben, Gesundheit und Glück bedeutet.

In Malayalam	ആയുരാരോഗ്യസൌഖ്യം
In Devanagari	आयुरारोग्यसौख्यम्
In IAST	yurārogyasaukhyam
Wert gemäß Kaṭapayādi	1712210

Diese Zahl ist die Zeit, zu der die Arbeit abgeschlossen war, dargestellt als Anzahl der Tage seit Beginn des Kali Yuga gemäß dem Malayalam-Kalender .

Andere

• Manche Leute verwenden das Kaṭapayādi- System bei der Benennung von Neugeborenen.
• Der folgende Vers, der in Malayalam von Koduṅṅallur Kuññikkuṭṭan Taṃpurān unter Verwendung von Kaṭapayādi zusammengestellt wurde, ist die Anzahl der Tage in den Monaten des Gregorianischen Kalenders .

പലഹാരേ പാലു നല്ലൂ, പുലർന്നാലോ കലക്കിലാം

ഇല്ലാ പാലെന്നു ഗോപാലൻ – ആംഗ്ലമാസദിനം ക്രമാൽ

Transiliteration

palahāre pālu nallū, pularnnālo kalakkilāṃ

illā pālennu gopālan – āṃgḷamāsadinaṃ kramāl

Übersetzung: Milch ist am besten zum Frühstück, wenn es morgens ist, sollte sie gerührt werden. Aber Gopālan sagt, es gibt keine Milch – die Anzahl der Tage der englischen Monate in Ordnung.

Umwandeln Paare von Buchstaben mit Kaṭapayādi Ausbeuten - Pala (പല) 31 ist , Haré (ഹാരേ) 28, PALU പാലു = 31, nallū (നല്ലൂ) 30, pular (പുലര്) 31 ist , nnālo (ന്നാലോ) 30, Kala ( കല) 31 ist , kkilāṃ (ക്കിലാം) 31 ist, Illā (ഇല്ലാ) 30, Pale (പാലെ) 31 ist , NNU zu gehen (ന്നു ഗോ) 30, PALAN (പാലന്) ist 31.

Siehe auch

Verweise

Weiterlesen

• AA Hattangadi, Explorations in Mathematics, Universities Press (India) Pvt. Ltd., Hyderabad (2001) ISBN  81-7371-387-1 [3]