Knotentheorie - Knot theory

Beispiele für verschiedene Knoten, einschließlich des Trivialknotens (oben links) und des Kleeblattknotens (darunter)

Ein Knotendiagramm des Kleeblattknotens, des einfachsten nicht-trivialen Knotens

Auf dem mathematischen Gebiet der Topologie ist die Knotentheorie das Studium mathematischer Knoten . Inspiriert von Knoten, die im täglichen Leben vorkommen, wie denen in Schnürsenkeln und Seilen, unterscheidet sich ein mathematischer Knoten dadurch, dass die Enden so verbunden sind, dass er nicht gelöst werden kann. Der einfachste Knoten ist ein Ring (oder "Knoten") . In der Sprache der Mathematik, ist ein Knoten eine Einbettung eines Kreises in 3-dimensionalen euklidischen Raum , (in der Topologie wird ein Kreis nicht auf das klassische geometrische Konzept gebunden, sondern an alle seine homeomorphisms ). Zwei mathematische Knoten sind äquivalent, wenn einer durch eine Verformung seiner selbst in den anderen umgewandelt werden kann (bekannt als Umgebungsisotopie ); diese Transformationen entsprechen Manipulationen an einer verknoteten Schnur, die nicht das Durchschneiden oder Durchlaufen derselben beinhalten. ${\displaystyle \mathbb{R} ^{3}}$${\displaystyle \mathbb{R} ^{3}}$

Knoten können auf verschiedene Weise beschrieben werden. Bei Verwendung unterschiedlicher Beschreibungsmethoden kann es mehr als eine Beschreibung desselben Knotens geben. Eine gängige Methode zum Beschreiben eines Knotens ist beispielsweise ein planares Diagramm, das als Knotendiagramm bezeichnet wird und in dem jeder Knoten auf viele verschiedene Arten gezeichnet werden kann. Daher besteht ein grundlegendes Problem in der Knotentheorie darin, zu bestimmen, wann zwei Beschreibungen denselben Knoten darstellen.

Für dieses Problem existiert eine vollständige algorithmische Lösung, deren Komplexität unbekannt ist . In der Praxis werden Knoten oft anhand einer Knoteninvariante unterschieden , einer "Menge", die gleich ist, wenn sie aus verschiedenen Knotenbeschreibungen berechnet wird. Wichtige Invarianten umfassen Knotenpolynome , Knotengruppen und hyperbolische Invarianten.

Die ursprüngliche Motivation für die Begründer der Knotentheorie war es, eine Tabelle von Knoten und Gliedern zu erstellen , die Knoten aus mehreren miteinander verschränkten Komponenten sind. Seit den Anfängen der Knotentheorie im 19. Jahrhundert wurden mehr als sechs Milliarden Knoten und Verbindungen tabellarisch erfasst .

Um weitere Erkenntnisse zu gewinnen, haben Mathematiker das Knotenkonzept auf verschiedene Weise verallgemeinert. Knoten können in anderen dreidimensionalen Räumen betrachtet werden und andere Objekte als Kreise können verwendet werden; siehe Knoten (Mathematik) . Höherdimensionale Knoten sind n- dimensionale Kugeln im m- dimensionalen euklidischen Raum.

Geschichte

Komplizierte keltische Knüpfarbeiten im 1200 Jahre alten Book of Kells

Archäologen haben herausgefunden, dass das Binden von Knoten bis in prähistorische Zeiten zurückreicht. Neben ihrer Verwendung wie dem Aufzeichnen von Informationen und dem Verbinden von Objekten haben Knoten die Menschen wegen ihrer Ästhetik und spirituellen Symbolik interessiert. Knoten erscheinen in verschiedenen Formen chinesischer Kunstwerke aus mehreren Jahrhunderten v. Chr. (siehe Chinesische Knoten ). Der endlose Knoten taucht im tibetischen Buddhismus auf , während die Borromäischen Ringe in verschiedenen Kulturen wiederholt aufgetaucht sind und oft Stärke in Einheit darstellen. Die keltischen Mönche, die das Book of Kells erschufen, haben ganze Seiten mit komplizierten keltischen Knüpfarbeiten verschwendet .

Der erste Knotentabulator, Peter Guthrie Tait

Eine mathematische Knotentheorie wurde erstmals 1771 von Alexandre-Théophile Vandermonde entwickelt, der bei der Diskussion der Eigenschaften von Knoten in Bezug auf die Positionsgeometrie ausdrücklich auf die Bedeutung topologischer Merkmale hinwies. Die mathematische Untersuchung von Knoten begann im 19. Jahrhundert mit Carl Friedrich Gauß , der das verbindende Integral definierte ( Silver 2006 ). In den 1860er Jahren, Lord Kelvin ‚s Theorie , dass Atome waren Knoten in dem Äther zu führte Peter Guthrie Tait ‘ s Gründung der ersten Knotentabellen für die vollständige Klassifikation. Tait veröffentlichte 1885 eine Knotentabelle mit bis zu zehn Kreuzungen und die sogenannten Tait-Vermutungen . Diese Aufzeichnung motivierte die frühen Knotentheoretiker, aber die Knotentheorie wurde schließlich Teil des aufkommenden Themas der Topologie .

Diese Topologen in der frühen Hälfte des 20. Jahrhunderts – Max Dehn , JW Alexander und andere – untersuchten Knoten aus der Sicht der Knotengruppe und Invarianten aus der Homologietheorie wie das Alexander-Polynom . Dies war der Hauptansatz der Knotentheorie, bis eine Reihe von Durchbrüchen das Thema veränderten.

In den späten 1970er Jahren führte William Thurston mit dem Hyperbolisierungssatz die hyperbolische Geometrie in die Untersuchung von Knoten ein . Es wurde gezeigt, dass viele Knoten hyperbolische Knoten sind , was die Verwendung von Geometrie ermöglicht, um neue, mächtige Knoteninvarianten zu definieren . Die Entdeckung des Jones-Polynoms durch Vaughan Jones im Jahr 1984 ( Sossinsky 2002 , S. 71–89) und nachfolgende Beiträge von Edward Witten , Maxim Kontsevich und anderen zeigten tiefe Verbindungen zwischen der Knotentheorie und mathematischen Methoden in der statistischen Mechanik und im Quantenfeld Theorie . Seitdem wurde eine Vielzahl von Knoteninvarianten erfunden, die ausgeklügelte Werkzeuge wie Quantengruppen und Floer-Homologie verwenden .

In den letzten Jahrzehnten des 20. Jahrhunderts interessierten sich Wissenschaftler für die Untersuchung physikalischer Knoten , um Knotenphänomene in DNA und anderen Polymeren zu verstehen . Die Knotentheorie kann verwendet werden, um zu bestimmen, ob ein Molekül chiral ist (eine "Händigkeit" hat) oder nicht ( Simon 1986 ). Tangles , Fäden, bei denen beide Enden fixiert sind, wurden effektiv beim Studium der Wirkung von Topoisomerase auf DNA verwendet ( Flapan 2000 ). Die Knotentheorie kann beim Bau von Quantencomputern durch das Modell der topologischen Quantenberechnung ( Collins 2006 ) entscheidend sein.

Knotenäquivalenz

Auf der linken Seite der Knoten und ein dazugehöriger Knoten. Es kann schwieriger zu bestimmen sein, ob komplexe Knoten, wie der rechte, dem Unknoten entsprechen.

Ein Knoten entsteht, indem man mit einem eindimensionalen Liniensegment beginnt , es willkürlich um sich selbst wickelt und dann seine beiden freien Enden zu einer geschlossenen Schleife verschmilzt ( Adams 2004 ) ( Sossinsky 2002 ). Wir können einfach sagen, ein Knoten ist eine "einfache geschlossene Kurve" oder "(geschlossene) Jordan-Kurve" (siehe Kurve ) - das heißt: eine "fast" injektive und stetige Funktion , wobei die einzige "Nicht-Injektivität" ist . Topologen betrachten Knoten und andere Verwicklungen wie Glieder und Zöpfe als gleichwertig, wenn der Knoten reibungslos, ohne sich zu kreuzen, herumgeschoben werden kann, um mit einem anderen Knoten zusammenzufallen. ${\displaystyle K}$ ${\displaystyle K\colon [0,1]\to\mathbb{R}^{3}}$${\displaystyle K(0)=K(1)}$

Die Idee der Knotenäquivalenz besteht darin, eine genaue Definition zu geben, wann zwei Knoten als gleich betrachtet werden sollten, auch wenn sie im Raum ganz unterschiedlich positioniert sind. Eine formale mathematische Definition ist, dass zwei Knoten äquivalent sind, wenn es einen orientierungserhaltenden Homöomorphismus mit gibt . ${\displaystyle K_{1},K_{2}}$ ${\displaystyle h\colon\mathbb{R}^{3}\to\mathbb{R}^{3}}$${\displaystyle h(K_{1})=K_{2}}$

Eine andere Möglichkeit, Knotenäquivalenz zu definieren, besteht darin, dass zwei Knoten äquivalent sind, wenn es eine kontinuierliche Familie von Raumhomöomorphismen auf sich selbst gibt, so dass der letzte von ihnen den ersten Knoten auf den zweiten Knoten trägt. (Formaler gesagt: Zwei Knoten und sind äquivalent, wenn es eine stetige Abbildung gibt, so dass a) für jede die Abbildung, die zu nimmt, ein Homöomorphismus von auf sich selbst ist; b) für alle ; und c) . Eine solche Funktion wird als Umgebungsisotopie bezeichnet .) ${\displaystyle \{h_{t}:\mathbb {R} ^{3}\rightarrow \mathbb {R} ^{3}\ \mathrm {für} \ 0\leq t\leq 1\}}$${\displaystyle K_{1}}$${\displaystyle K_{2}}$${\displaystyle H:\mathbb{R}^{3}\times [0,1]\rightarrow\mathbb{R}^{3}}$${\displaystyle t\in [0,1]}$${\displaystyle x\in\mathbb{R} ^{3}}$${\displaystyle H(x,t)\in\mathbb{R}^{3}}$${\displaystyle \mathbb{R} ^{3}}$${\displaystyle H(x,0)=x}$${\displaystyle x\in\mathbb{R} ^{3}}$${\displaystyle H(K_{1},1)=K_{2}}$${\displaystyle H}$

Diese beiden Begriffe der Knotenäquivalenz stimmen genau darin überein, welche Knoten äquivalent sind: Zwei Knoten, die unter der Definition des orientierungserhaltenden Homöomorphismus äquivalent sind, sind auch unter der Definition der Umgebungsisotopie äquivalent, da jeder orientierungserhaltende Homöomorphismus für sich selbst die Endstufe von an . ist Umgebungsisotopie ausgehend von der Identität. Umgekehrt sind zwei Knoten, die unter der Definition der Umgebungsisotopie äquivalent sind, auch unter der Definition des orientierungserhaltenden Homöomorphismus äquivalent, da die (End-)Stufe der Umgebungsisotopie ein orientierungserhaltender Homöomorphismus sein muss, der einen Knoten zum anderen trägt. ${\displaystyle \mathbb{R} ^{3}}$${\displaystyle t=1}$

Das Grundproblem der Knotentheorie, das Erkennungsproblem , ist die Bestimmung der Äquivalenz zweier Knoten. Es gibt Algorithmen , um dieses Problem zu lösen, wobei der erste von Wolfgang Haken in den späten 1960er Jahren gegeben wurde ( Hass 1998 ). Nichtsdestotrotz können diese Algorithmen extrem zeitaufwändig sein, und ein Hauptproblem in der Theorie besteht darin, zu verstehen, wie schwer dieses Problem wirklich ist ( Hass 1998 ). Der Sonderfall der Anerkennung unknot , die genannt unknotting Problem , ist von besonderem Interesse ( Hoste 2005 ). Im Februar 2021 kündigte Marc Lackenby einen neuen Unnot-Erkennungsalgorithmus an, der in quasi-polynomialer Zeit läuft .

Knotendiagramme

Eine nützliche Möglichkeit, Knoten zu visualisieren und zu manipulieren, besteht darin, den Knoten auf eine Ebene zu projizieren – denken Sie daran, dass der Knoten einen Schatten an die Wand wirft. Eine kleine Änderung der Projektionsrichtung stellt sicher, dass es eins zu eins ist, außer an den Doppelpunkten, den sogenannten Kreuzungen , wo sich der "Schatten" des Knotens einmal quer kreuzt ( Rolfsen 1976 ). Um den ursprünglichen Knoten wieder herstellen zu können, muss bei jeder Kreuzung der Oberstrang vom Unterstrang unterschieden werden. Dies geschieht oft, indem eine Unterbrechung in der darunter liegenden Strähne erzeugt wird. Das resultierende Diagramm ist eine eingetauchte ebene Kurve mit den zusätzlichen Daten, welcher Strang bei jeder Kreuzung über und welcher unter ist. (Diese Diagramme werden Knotendiagramme genannt, wenn sie einen Knoten darstellen, und Verknüpfungsdiagramme, wenn sie eine Verknüpfung darstellen .) Analog können geknotete Flächen im 4-Raum mit eingetauchten Flächen im 3-Raum in Beziehung gesetzt werden.

Ein reduziertes Diagramm ist ein Knotendiagramm, in dem keine reduzierbaren Kreuzungen (auch nugatorische oder entfernbare Kreuzungen ) vorhanden sind oder in dem alle reduzierbaren Kreuzungen entfernt wurden. Eine Blütenblattprojektion ist eine Art von Projektion, bei der sich, anstatt Doppelpunkte zu bilden, alle Stränge des Knotens an einem einzigen Kreuzungspunkt treffen, der durch Schlaufen verbunden ist, die nicht verschachtelte "Blütenblätter" bilden.

Reidemeister zieht um

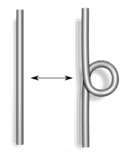
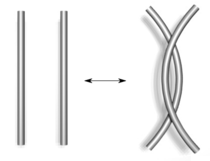
Im Jahr 1927 demonstrierten JW Alexander und Garland Baird Briggs und unabhängig voneinander Kurt Reidemeister mit dieser schematischen Form von Knoten, dass zwei Knotendiagramme, die zu demselben Knoten gehören, durch eine Folge von drei Arten von Zügen auf dem unten gezeigten Diagramm in Beziehung gesetzt werden können . Diese Operationen, die jetzt als Reidemeister-Züge bezeichnet werden , sind:

Reidemeister zieht um

Tippe I	Typ II
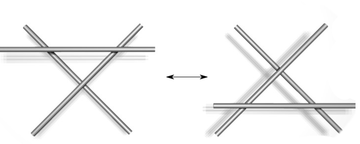
Typ III

Der Beweis, dass Diagramme äquivalenter Knoten durch Reidemeister-Bewegungen verbunden sind, beruht auf einer Analyse dessen, was unter der planaren Projektion der Bewegung passiert, die einen Knoten zum anderen führt. Die Bewegung kann so angeordnet werden, dass die Projektion fast immer ein Knotendiagramm ist, außer in endlich vielen Fällen, wenn ein "Ereignis" oder eine "Katastrophe" eintritt, beispielsweise wenn sich mehr als zwei Stränge an einem Punkt kreuzen oder mehrere Stränge an einem Punkt tangential werden. Eine genaue Betrachtung wird zeigen, dass komplizierte Ereignisse eliminiert werden können, wobei nur die einfachsten Ereignisse übrig bleiben: (1) ein "Knick", der sich bildet oder begradigt wird; (2) zwei Stränge, die an einem Punkt tangential werden und hindurchgehen; und (3) drei Stränge, die sich an einem Punkt kreuzen. Dies sind genau die Reidemeister-Bewegungen ( Sossinsky 2002 , Kap. 3) ( Lickorish 1997 , Kap. 1).

Knoteninvarianten

Eine Knoteninvariante ist eine „Menge“, die für äquivalente Knoten gleich ist ( Adams 2004 ) ( Lickorish 1997 ) ( Rolfsen 1976 ). Wenn die Invariante beispielsweise aus einem Knotendiagramm berechnet wird, sollte sie den gleichen Wert für zwei Knotendiagramme ergeben, die äquivalente Knoten darstellen. Eine Invariante kann auf zwei verschiedenen Knoten denselben Wert annehmen, kann also allein nicht in der Lage sein, alle Knoten zu unterscheiden. Eine elementare Invariante ist die Dreifärbbarkeit .

"Klassische" Knoteninvarianten umfassen die Knotengruppe , die die Fundamentalgruppe des Knotenkomplements ist , und das Alexander-Polynom , das aus der Alexander-Invariante berechnet werden kann, einem Modul, das aus der unendlichen zyklischen Abdeckung des Knotenkomplements konstruiert wurde ( Lickorish 1997 ) ( Rolfsen 1976 ). Im späten 20. Jahrhundert wurden Invarianten wie "Quanten"-Knotenpolynome, Vassiliev-Invarianten und hyperbolische Invarianten entdeckt. Diese oben genannten Invarianten sind nur die Spitze des Eisbergs der modernen Knotentheorie.

Knotenpolynome

Ein Knotenpolynom ist eine Knoteninvariante , die ein Polynom ist . Bekannte Beispiele sind die Jones- und Alexander-Polynome . Eine Variante des Alexander-Polynoms, das Alexander-Conway-Polynom , ist ein Polynom in der Variablen z mit ganzzahligen Koeffizienten ( Lickorish 1997 ).

Das Alexander-Conway-Polynom ist eigentlich in Bezug auf Verbindungen definiert , die aus einem oder mehreren miteinander verschränkten Knoten bestehen. Die oben für Knoten erklärten Konzepte, zB Diagramme und Reidemeister-Züge, gelten auch für Links.

Betrachten Sie ein orientiertes Link-Diagramm, dh eines, bei dem jede Komponente des Links eine Vorzugsrichtung hat, die durch einen Pfeil angezeigt wird. Für eine gegebene Kreuzung des Diagramms seien die orientierten Verbindungsdiagramme, die sich aus der Änderung des Diagramms ergeben, wie in der Abbildung angegeben: ${\displaystyle L_{+},L_{-},L_{0}}$

Das ursprüngliche Diagramm kann entweder oder sein , abhängig von der Konfiguration der gewählten Kreuzung. Dann wird das Alexander-Conway-Polynom, , rekursiv nach den Regeln definiert: ${\displaystyle L_{+}}$${\displaystyle L_{-}}$${\displaystyle C(z)}$

• ${\displaystyle C(O)=1}$(wo ist ein Diagramm des Unknotens )${\displaystyle O}$
• ${\displaystyle C(L_{+})=C(L_{-})+zC(L_{0}).}$

Die zweite Regel ist das, was oft als Strangrelation bezeichnet wird . Um zu überprüfen, ob diese Regeln eine Invariante einer orientierten Verknüpfung ergeben, sollte man feststellen, dass sich das Polynom unter den drei Reidemeister-Zügen nicht ändert. Viele wichtige Knotenpolynome können auf diese Weise definiert werden.

Das Folgende ist ein Beispiel für eine typische Berechnung unter Verwendung einer Strangbeziehung. Es berechnet das Alexander-Conway-Polynom des Kleeblattknotens . Die gelben Felder zeigen an, wo die Relation angewendet wird.

C ( ) =  C ( ) +  z C ( )

gibt den unknot und den Hopf-Link . Anwenden der Beziehung zum Hopf-Link, wo angegeben,

C ( ) = C ( ) + z C ( )

gibt eine verformbare Verbindung zu einer mit 0 Kreuzungen (es ist eigentlich die Trennung von zwei Komponenten) und eine Unknotung. Das Aufheben der Verknüpfung erfordert ein wenig Hinterhältigkeit:

C ( ) = C ( ) + z C ( )

was impliziert, dass C (unlink of two components) = 0 ist, da die ersten beiden Polynome vom Unknoten sind und somit gleich sind.

Wenn man all dies zusammenfasst, zeigt sich:

${\displaystyle C(\mathrm{Kleeblatt})=1+z(0+z)=1+z^{2}}$

Da das Alexander-Conway-Polynom eine Knoteninvariante ist, zeigt dies, dass das Kleeblatt nicht dem Unknoten entspricht. Das Kleeblatt ist also wirklich "geknotet".

• 

  Der linkshändige Kleeblattknoten.

• 

  Der rechtshändige Kleeblattknoten.

Tatsächlich gibt es zwei Kleeblattknoten, die als rechts- und linkshändige Kleeblätter bezeichnet werden und die Spiegelbilder voneinander sind (nehmen Sie ein Diagramm des oben angegebenen Kleeblatts und ändern Sie jede Kreuzung in die andere Richtung, um das Spiegelbild zu erhalten). Diese sind einander nicht äquivalent, dh sie sind nicht amphichiral. Dies wurde von Max Dehn vor der Erfindung der Knotenpolynome mit gruppentheoretischen Methoden gezeigt ( Dehn 1914 ). Aber das Alexander-Conway-Polynom jeder Art von Kleeblatt wird gleich sein, wie man sieht, wenn man die obige Berechnung mit dem Spiegelbild durchgeht. Das Jones- Polynom kann tatsächlich zwischen den links- und rechtshändigen Kleeblattknoten unterscheiden ( Lickorish 1997 ).

Hyperbolische Invarianten

William Thurston bewies, dass viele Knoten hyperbolische Knoten sind , was bedeutet, dass das Knotenkomplement (dh die Menge der Punkte des 3-Raums nicht auf dem Knoten) eine geometrische Struktur zulässt, insbesondere die der hyperbolischen Geometrie . Die hyperbolische Struktur hängt nur vom Knoten ab, daher ist jede aus der hyperbolischen Struktur berechnete Größe eine Knoteninvariante ( Adams 2004 ).

Die Borromäischen Ringe sind eine Verbindung mit der Eigenschaft, dass das Entfernen eines Rings die anderen auflöst.

Die Spitzenansicht von SnapPea : Die Borromäischen Ringe ergänzen sich aus der Perspektive eines Bewohners, der in der Nähe der roten Komponente lebt.

Geometrie lässt uns visualisieren, wie das Innere eines Knoten- oder Verbindungskomplements aussieht, indem wir uns Lichtstrahlen vorstellen, die entlang der Geodäten der Geometrie wandern. Ein Beispiel liefert das Bild des Komplements der Borromäischen Ringe . Der Bewohner dieser Linkergänzung betrachtet den Raum aus der Nähe der roten Komponente. Die Bälle im Bild sind Ansichten von Horoball- Nachbarschaften des Links. Durch das Verdicken des Glieds in einer üblichen Weise werden die Horoball-Nachbarschaften der Gliedkomponenten erhalten. Auch wenn die Grenze einer Nachbarschaft ein Torus ist, sieht sie von innen betrachtet wie eine Kugel aus. Jede Verbindungskomponente zeigt so unendlich viele Kugeln (einer Farbe), wie es unendlich viele Lichtstrahlen vom Beobachter zur Verbindungskomponente gibt. Das Fundamentalparallelogramm (das im Bild angezeigt wird) kachelt sowohl vertikal als auch horizontal und zeigt, wie das Kugelmuster unendlich erweitert werden kann.

Dieses Muster, das Horoball-Muster, ist selbst eine nützliche Invariante. Andere hyperbolische Invarianten umfassen die Form des Fundamentalparallelogramms, die Länge der kürzesten Geodäten und das Volumen. Moderne Knoten- und Verknüpfungstabellenarbeiten haben diese Invarianten effektiv genutzt. Schnelle Computer und clevere Methoden zum Erhalten dieser Invarianten machen die Berechnung dieser Invarianten in der Praxis zu einer einfachen Aufgabe ( Adams, Hildebrand & Weeks 1991 ).

Höhere Abmessungen

Ein Knoten in drei Dimensionen kann gelöst werden, wenn er im vierdimensionalen Raum platziert wird. Dies geschieht durch das Wechseln von Kreuzungen. Angenommen, ein Strang befindet sich von einem ausgewählten Punkt aus gesehen hinter einem anderen. Heben Sie es in die vierte Dimension, damit es kein Hindernis gibt (der vordere Strang hat dort keine Komponente); Dann schieben Sie es nach vorne und lassen Sie es zurück, jetzt vorne. Analogien für die Ebene wären das Anheben einer Schnur von der Oberfläche oder das Entfernen eines Punkts aus einem Kreis.

Tatsächlich entspricht in vier Dimensionen jede sich nicht schneidende geschlossene Schleife eines eindimensionalen Strings einem Unknoten. Zuerst "schieben" Sie die Schleife in einen dreidimensionalen Unterraum, was immer möglich ist, wenn auch technisch zu erklären.

Knüpfkugeln höherer Dimension

Da ein Knoten topologisch als 1-dimensionale Kugel betrachtet werden kann, besteht die nächste Verallgemeinerung darin, eine zweidimensionale Kugel ( ) eingebettet in einen 4-dimensionalen euklidischen Raum ( ) zu betrachten. Eine solche Einbettung ist verknotet, wenn es keinen Homöomorphismus gibt , die eingebettete 2-Kugel auf sich selbst zu der standardmäßigen "runden" Einbettung der 2-Kugel zu bringen. Hängeknoten und Spinnknoten sind zwei typische Familien solcher 2-Kugel-Knoten. ${\displaystyle \mathbb{S} ^{2}}$${\displaystyle \mathbb{R} ^{4}}$${\displaystyle \mathbb{R} ^{4}}$

Die als "allgemeine Position" bezeichnete mathematische Technik impliziert, dass für eine gegebene n- Kugel im m- dimensionalen euklidischen Raum, wenn m groß genug ist (abhängig von n ), die Kugel entknotet werden sollte. Im Allgemeinen bilden stückweise lineare n- Kugeln nur im ( n  + 2)-dimensionalen Raum Knoten ( Zeeman 1963 ), obwohl dies für glatt verknotete Kugeln nicht mehr erforderlich ist. Tatsächlich gibt es im 6k- dimensionalen Raum glatt verknotete Kugeln ; zB gibt es eine glatt verknotete 3-Kugel in ( Haefliger 1962 ) ( Levine 1965 ). Somit kann die Kodimension eines glatten Knotens beliebig groß sein, wenn die Dimension der geknoteten Kugel nicht festgelegt ist; jedoch ist jede glatte k- Kugel, die in mit eingebettet ist, ungeknotet. Der Begriff Knoten hat weitere Verallgemeinerungen in der Mathematik, siehe: Knoten (Mathematik) , Isotopenklassifikation von Einbettungen . ${\displaystyle (4k-1)}$${\displaystyle \mathbb{R} ^{6}}$${\displaystyle \mathbb{R} ^{n}}$${\displaystyle 2n-3k-3>0}$

Jeder Knoten in der n- Sphäre ist das Glied einer reell-algebraischen Menge mit isolierter Singularität in ( Akbulut & King 1981 ). ${\displaystyle \mathbb{S} ^{n}}$${\displaystyle \mathbb{R} ^{n+1}}$

Ein n- Knoten ist ein einzelner in . Ein n- Link besteht aus k- Kopien von eingebettet in , wobei k eine natürliche Zahl ist . Sowohl die Fälle als auch die Fälle sind gut untersucht, und das ist auch der Fall. ${\displaystyle \mathbb{S} ^{n}}$${\displaystyle \mathbb{R} ^{m}}$${\displaystyle \mathbb{S} ^{n}}$${\displaystyle \mathbb{R} ^{m}}$${\displaystyle m=n+2}$${\displaystyle m>n+2}$${\displaystyle n>1}$

Knoten hinzufügen

Hinzufügen von zwei Knoten

Zwei Knoten können hinzugefügt werden, indem beide Knoten geschnitten und die Endenpaare verbunden werden. Die Operation wird als Knotensumme oder manchmal als verbundene Summe oder Zusammensetzung zweier Knoten bezeichnet. Dies kann formal wie folgt definiert werden ( Adams 2004 ): Betrachten Sie eine planare Projektion jedes Knotens und nehmen Sie an, dass diese Projektionen disjunkt sind. Finden Sie ein Rechteck in der Ebene, in dem ein Paar gegenüberliegender Seiten Bögen entlang jedes Knotens sind, während der Rest des Rechtecks ​​von den Knoten getrennt ist. Bilden Sie einen neuen Knoten, indem Sie das erste Paar gegenüberliegender Seiten löschen und das andere Paar gegenüberliegender Seiten anschließen. Der resultierende Knoten ist eine Summe der ursprünglichen Knoten. Je nachdem, wie dies gemacht wird, können sich zwei verschiedene Knoten (aber nicht mehr) ergeben. Diese Mehrdeutigkeit in der Summe kann beseitigt werden, wenn die Knoten orientiert sind , dh eine bevorzugte Bewegungsrichtung entlang des Knotens aufweisen und erfordern, dass die Bögen der Knoten in der Summe konsistent mit der orientierten Grenze des Rechtecks ​​orientiert sind.

Die Knotensumme orientierter Knoten ist kommutativ und assoziativ . Ein Knoten ist prim, wenn er nicht trivial ist und nicht als Knotensumme zweier nicht trivialer Knoten geschrieben werden kann. Ein Knoten, der als solche Summe geschrieben werden kann, ist zusammengesetzt . Für Knoten gibt es eine Primzerlegung, analog zu Prim- und zusammengesetzten Zahlen ( Schubert 1949 ). Für orientierte Knoten ist diese Zerlegung ebenfalls eindeutig. Es können auch höherdimensionale Knoten hinzugefügt werden, aber es gibt einige Unterschiede. Während Sie den Knoten in drei Dimensionen nicht durch Hinzufügen von zwei nicht-trivialen Knoten bilden können, können Sie dies in höheren Dimensionen, zumindest wenn man glatte Knoten in der Kodimension von mindestens 3 betrachtet.

Tabellieren von Knoten

Eine Tabelle mit Primknoten bis zu sieben Kreuzungen. Die Knoten sind mit der Alexander-Briggs-Notation beschriftet

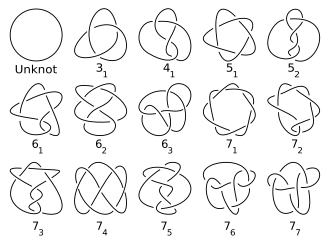
Traditionell werden Knoten nach Kreuzungszahlen katalogisiert . Knotentabellen enthalten im Allgemeinen nur Primknoten und nur einen Eintrag für einen Knoten und sein Spiegelbild (auch wenn sie unterschiedlich sind) ( Hoste, Thistlethwaite & Weeks 1998 ). Die Anzahl der nichttrivialen Knoten einer gegebenen Kreuzungszahl nimmt schnell zu, was die tabellarische Berechnung rechnerisch erschwert ( Hoste 2005 , S. 20). Es gelang, über 6 Milliarden Knoten und Verbindungen aufzuzählen ( Hoste 2005 , S. 28). Die Reihenfolge der Anzahl der Primknoten einer gegebenen Kreuzungsnummer bis zur Kreuzungsnummer 16 ist 0, 0, 1, 1, 2, 3, 7, 21, 49, 165, 552, 2176, 9988,46 972 ,253 293 ,1 388 705 ... (Sequenz A002863 im OEIS ). Obwohl exponentielle obere und untere Schranken für diese Folge bekannt sind, ist nicht bewiesen, dass diese Folge streng ansteigend ist ( Adams 2004 ).

Die ersten Knotentabellen von Tait, Little und Kirkman verwendeten Knotendiagramme, obwohl Tait auch einen Vorläufer der Dowker-Notation verwendete . Für Knoten wurden verschiedene Notationen erfunden, die eine effizientere Tabellierung ermöglichen ( Hoste 2005 ).

Die frühen Tabellen versuchten, alle Knoten von höchstens 10 Kreuzungen und alle alternierenden Knoten von 11 Kreuzungen aufzulisten ( Hoste, Thistlethwaite & Weeks 1998 ). Die Entwicklung der Knotentheorie durch Alexander, Reidemeister, Seifert und andere erleichterte die Verifikation und Knotentabellen bis einschließlich 9 Kreuzungen wurden Ende der 1920er Jahre von Alexander-Briggs und Reidemeister veröffentlicht.

Die erste große Verifizierung dieser Arbeit erfolgte in den 1960er Jahren durch John Horton Conway , der nicht nur eine neue Notation, sondern auch das Alexander-Conway-Polynom ( Conway 1970 ) entwickelte ( Doll & Hoste 1991 ). Dies verifizierte die Knotenliste von höchstens 11 Kreuzungen und eine neue Liste von Verbindungen bis zu 10 Kreuzungen. Conway fand eine Reihe von Auslassungen, aber nur eine Duplizierung in den Tait-Little-Tabellen; er vermisste jedoch die Duplikate namens Perko-Paar , die erst 1974 von Kenneth Perko ( Perko 1974 ) bemerkt wurden . Dieser berühmte Fehler verbreitete sich, als Dale Rolfsen in seinem einflussreichen Text, der auf Conways Arbeit basierte, eine Knotentabelle hinzufügte. Conways Aufsatz zur Knotentheorie aus dem Jahr 1970 enthält auch eine typografische Vervielfältigung auf seiner nicht abwechselnden Seite mit 11 kreuzenden Knoten und lässt 4 Beispiele weg – 2 wurden zuvor in D. Lombarderos Abschlussarbeit in Princeton von 1968 aufgeführt und 2 weitere wurden später von Alain Caudron entdeckt . [siehe Perko (1982), Primalität bestimmter Knoten, Topology Proceedings] Weniger bekannt ist das Duplikat in seiner 10 Crossing Link Table: 2.-2.-20.20 ist der Spiegel von 8*-20:-20. [Siehe Perko (2016), Historische Highlights der nicht-zyklischen Knotentheorie, J. Knot Theory Ramifications].

In den späten 1990er Jahren haben Hoste, Thistlethwaite und Weeks alle Knoten durch 16 Kreuzungen tabelliert ( Hoste, Thistlethwaite & Weeks 1998 ). 2003 haben Rankin, Flint und Schermann die alternierenden Knoten durch 22 Kreuzungen tabelliert ( Hoste 2005 ).

Alexander-Briggs-Notation

Dies ist die traditionellste Notation, die auf den Artikel von James W. Alexander und Garland B. Briggs aus dem Jahr 1927 zurückgeht und später von Dale Rolfsen in seiner Knotentabelle erweitert wurde (siehe Bild oben und Liste der Primknoten ). Die Notation organisiert Knoten einfach nach ihrer Kreuzungsnummer. Man schreibt die Kreuzungsnummer mit einem Index, um ihre Reihenfolge unter allen Knoten mit dieser Kreuzungsnummer anzugeben. Diese Reihenfolge ist willkürlich und hat daher keine besondere Bedeutung (obwohl bei jeder Anzahl von Kreuzungen der Twist-Knoten nach dem Torus-Knoten kommt ). Links werden durch die Kreuzungsnummer mit einem hochgestellten Index geschrieben, um die Anzahl der Komponenten anzugeben, und einem tiefgestellten Index, um die Reihenfolge innerhalb der Links mit der gleichen Anzahl von Komponenten und Kreuzungen anzugeben. Somit wird der Kleeblattknoten mit 3 ₁ notiert und der Hopf-Link ist 2²
₁. Alexander-Briggs-Namen im Bereich von 10 ₁₆₂ bis 10 ₁₆₆ sind aufgrund der Entdeckung des Perko-Paares in Charles Newton Littles ursprünglichen und nachfolgenden Knotentabellen und der unterschiedlichen Vorgehensweise zur Korrektur dieses Fehlers in Knotentabellen und anderen erstellten Veröffentlichungen mehrdeutig nach diesem Punkt.

Dowker-Thistlethwaite-Notation

Ein Knotendiagramm mit Kreuzungen, die für eine Dowker-Folge beschriftet sind

Die Dowker-Thistlethwaite-Notation , auch Dowker-Notation oder Code genannt, für einen Knoten ist eine endliche Folge von geraden ganzen Zahlen. Die Zahlen werden erzeugt, indem man dem Knoten folgt und die Kreuzungen mit aufeinanderfolgenden ganzen Zahlen markiert. Da jede Kreuzung zweimal besucht wird, entsteht eine Paarung von geraden ganzen Zahlen mit ungeraden ganzen Zahlen. Über- und Unterquerungen sind durch entsprechende Schilder gekennzeichnet. In dieser Abbildung hat das Knotendiagramm zum Beispiel Kreuzungen, die mit den Paaren (1,6) (3,−12) (5,2) (7,8) (9,−4) und (11,−10) beschriftet sind. Die Dowker-Thistlethwaite-Notation für diese Beschriftung ist die Sequenz: 6, −12, 2, 8, −4, −10. Ein Knotendiagramm hat mehr als eine mögliche Dowker-Notation, und es gibt eine wohlverstandene Mehrdeutigkeit, wenn man einen Knoten aus einer Dowker-Thistlethwaite-Notation rekonstruiert.

Conway-Notation

Die nach John Horton Conway benannte Conway-Notation für Knoten und Glieder basiert auf der Tangles- Theorie ( Conway 1970 ). Der Vorteil dieser Notation besteht darin, dass sie einige Eigenschaften des Knotens oder der Verbindung widerspiegelt.

Die Notation beschreibt, wie ein bestimmtes Linkdiagramm des Links erstellt wird. Beginnen mit einem Grund - Polyeder , ein 4-wertiges verbunden planaren Graphen ohne Digon Regionen. Ein solches Polyeder wird zuerst durch die Anzahl der Scheitelpunkte und dann durch die Anzahl der Sternchen gekennzeichnet, die die Position des Polyeders auf einer Liste von Basispolyedern bestimmen. 10** bezeichnet zum Beispiel das zweite 10-Scheitel-Polyeder auf Conways Liste.

In jede Ecke wird dann ein algebraisches Knäuel eingesetzt (jede Ecke ist so ausgerichtet, dass es keine willkürliche Wahl der Ersetzung gibt). Jedes solche Gewirr hat eine Notation bestehend aus Zahlen und + oder − Zeichen.

Ein Beispiel ist 1*2 −3 2. Die 1* bezeichnet das einzige 1-Eck-Basispolyeder. Die 2 −3 2 ist eine Folge, die den Kettenbruch beschreibt, der einem rationalen Knäuel zugeordnet ist . Man fügt dieses Knäuel am Scheitelpunkt des Grundpolyeders 1* ein.

Ein komplizierteres Beispiel ist 8*3.1.2 0.1.1.1.1.1 Auch hier bezieht sich 8* auf ein Grundpolyeder mit 8 Ecken. Die Punkte trennen die Notation für jedes Tangle.

Jeder Link lässt eine solche Beschreibung zu, und es ist klar, dass dies selbst für sehr große Kreuzungszahlen eine sehr kompakte Notation ist. Es gibt einige weitere Abkürzungen, die normalerweise verwendet werden. Das letzte Beispiel wird normalerweise 8*3:2 0 geschrieben, wobei die Einsen weggelassen werden und die Anzahl der Punkte mit Ausnahme der Punkte am Ende beibehalten wird. Bei einem algebraischen Knoten wie im ersten Beispiel wird 1* oft weggelassen.

Conways bahnbrechende Arbeit zu diesem Thema listet bis zu 10-Scheitel-Basispolyeder auf, die er verwendet, um Links zu tabellieren, die für diese Links zum Standard geworden sind. Für eine weitere Auflistung von Polyedern mit höheren Scheitelpunkten stehen nicht standardmäßige Auswahlmöglichkeiten zur Verfügung.

Gauss-Code

Gauss-Code , ähnlich der Dowker-Thistlethwaite-Notation, repräsentiert einen Knoten mit einer Folge von ganzen Zahlen. Anstatt jedoch jede Kreuzung durch zwei verschiedene Zahlen darzustellen, werden Kreuzungen mit nur einer Zahl gekennzeichnet. Wenn die Kreuzung eine Überkreuzung ist, wird eine positive Zahl aufgeführt. Bei einer Unterkreuzung eine negative Zahl. Zum Beispiel kann der Kleeblattknoten im Gauss-Code wie folgt angegeben werden: 1,−2,3,−1,2,−3

Gauss-Code ist in seiner Fähigkeit, Knoten zu identifizieren, eingeschränkt. Dieses Problem wird teilweise durch den erweiterten Gauss-Code behoben .

Siehe auch

• Schaltungstopologie
• Kontaktgeometrie#Legendrian Untermannigfaltigkeiten und Knoten
• Knoten und Grafiken
• Liste der Themen zur Knotentheorie
• Molekularer Knoten
• Quantentopologie
• Bandtheorie
• Krawatte § Knotenarten

Verweise

Quellen

• Adams, Colin (2004), The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots , American Mathematical Society , ISBN 978-0-8218-3678-1
• Adams, Colin ; Crawford, Thomas; DeMeo, Benjamin; Landry, Michael; Lin, Alex Tong; Montee, MurphyKate; Park, Seojung; Venkatesh, Saraswathi; Yhee, Farrah (2015), "Knot Projects with a single multi-crossing", Journal of Knot Theory and its Ramifications , 24 (3): 1550011, 30, arXiv : 1208.5742 , doi : 10.1142/S021821651550011X , MR  3342136
• Adams, Colin; Hildebrand, Martin; Weeks, Jeffrey (1991), "Hyperbolic invariants of knots and links", Transactions of the American Mathematical Society , 326 (1): 1–56, doi : 10.1090/s0002-9947-1991-0994161-2 , JSTOR  2001854
• Akbulut, Selman ; King, Henry C. (1981), "Alle Knoten sind algebraisch", Comm. Mathematik. Helv. , 56 (3): 339–351, doi : 10.1007/BF02566217
• Bar-Natan, Dror (1995), "On the Vassiliev knot invariants", Topology , 34 (2): 423–472, doi : 10.1016/0040-9383(95)93237-2
• Collins, Graham (April 2006), "Computing with Quantum Knots", Scientific American , 294 (4), S. 56–63, Bibcode : 2006SciAm.294d..56C , doi : 10.1038/scientificamerican0406-56
• Dehn, Max (1914), "Die beiden Kleeblattschlingen", Mathematische Annalen , 75 : 402–413
• Conway, John Horton (1970), „An enumeration of knots and links, and some of their algebraic properties“, Computational Problems in Abstract Algebra , Pergamon, S. 329–358, ISBN 978-0080129754, OCLC  322649
• Puppe, Helmut; Hoste, Jim (1991), „Eine tabellarische Aufstellung orientierter Links. Mit Mikrofiche-Beilage“, Math. Komp. , 57 (196): 747–761, Bibcode : 1991MaCom..57..747D , doi : 10.1090/S0025-5718-1991-1094946-4
• Flapan, Erica (2000), Wenn Topologie auf Chemie trifft: Ein topologischer Blick auf molekulare Chiralität , Ausblick, Cambridge University Press , ISBN 978-0-521-66254-3
• Haefliger, André (1962), "Knotted (4 k  − 1)-spheres in 6 k -space", Annals of Mathematics , Second Series, 75 (3): 452–466, doi : 10.2307/1970208 , JSTOR  1970208
• Hass, Joel (1998), "Algorithmen zur Erkennung von Knoten und 3-Mannigfaltigkeiten", Chaos, Solitons and Fractals , 9 (4–5): 569–581, arXiv : math/9712269 , Bibcode : 1998CSF.....9 ..569H , doi : 10.1016/S0960-0779(97)00109-4
• Hoste, Jim; Distelthwaite, Morwen ; Wochen, Jeffrey (1998), "Die ersten 1.701.935 Knoten", Math. Intelligencer , 20 (4): 33–48, doi : 10.1007/BF03025227
• Hoste, Jim (2005), "Die Aufzählung und Klassifikation von Knoten und Verbindungen", Handbook of Knot Theory (PDF) , Amsterdam: Elsevier
• Levine, Jerome (1965), "Eine Klassifikation differenzierbarer Knoten", Annals of Mathematics , Second Series, 1982 (1): 15–50, doi : 10.2307/1970561 , JSTOR  1970561
• Kontsevich, Maxim (1993), "Vassilievs Knoteninvarianten", IM Gelfand Seminar, Adv. Sowjetische Mathematik. , 2, Providence, RI: American Mathematical Society, 16 : 137–150, doi : 10.1090/advsov/016.2/04 , ISBN 9780821841174
• Lickorish, WB Raymond (1997), An Introduction to Knot Theory , Graduate Texts in Mathematics, Springer-Verlag, ISBN 978-0-387-98254-0
• Perko, Kenneth (1974), „Über die Klassifikation von Knoten“, Proceedings of the American Mathematical Society , 45 (2): 262–6, doi : 10.2307/2040074 , JSTOR  2040074
• Rolfsen, Dale (1976), Knots and Links , Mathematics Lecture Series, 7 , Berkeley, California : Publish or Perish, ISBN 978-0-914098-16-4, MR  0515288
• Schubert, Horst (1949), "Die eindeutige Zerlegbarkeit eines Knotens in Primknoten", Heidelberger Akad. Wiss. Math.-Nat. Kl. (3): 57–104
• Silver, Dan (2006), "Die ungeraden Ursprünge der Knotentheorie" (PDF) , American Scientist , 94 (2), S. 158–165, doi : 10.1511/2006.2.158
• Simon, Jonathan (1986), "Topologische Chiralität bestimmter Moleküle", Topology , 25 (2): 229–235, doi : 10.1016/0040-9383(86)90041-8
• Sossinsky, Alexei (2002), Knoten, Mathematik mit einem Twist , Harvard University Press, ISBN 978-0-674-00944-8
• Turaev, VG (1994), "Quantum invariants of knots and 3-manifolds" , De Gruyter Studies in Mathematics , Berlin: Walter de Gruyter & Co., 18 , arXiv : hep-th/9409028 , ISBN 978-3-11-013704-0
• Weisstein, Eric W. (2013). "Reduziertes Knotendiagramm" . MathWorld . Wolfram . Abgerufen am 8. Mai 2013 .
• Weisstein, Eric W. (2013a). "Reduzierbare Überfahrt" . MathWorld . Wolfram . Abgerufen am 8. Mai 2013 .
• Witten, Edward (1989), "Quantenfeldtheorie und das Jones-Polynom", Comm. Mathematik. Phys. , 121 (3): 351–399, Bibcode : 1989CMaPh.121..351W , doi : 10.1007/BF01217730
• Zeeman, EC (1963), "Unknotting combinatorial balls", Annals of Mathematics , Second Series, 78 (3): 501–526, doi : 10.2307/1970538 , JSTOR  1970538

Fußnoten

Weiterlesen

Einführende Lehrbücher

Es gibt eine Reihe von Einführungen in die Knotentheorie. Eine klassische Einführung für Doktoranden oder fortgeschrittene Bachelor ist ( Rolfsen 1976 ). Andere gute Texte aus den Referenzen sind ( Adams 2001 ) und ( Lickorish 1997 ). Adams ist informell und zum größten Teil für Gymnasiasten zugänglich. Lickorish ist eine rigorose Einführung für Doktoranden, die eine schöne Mischung aus klassischen und modernen Themen abdeckt. Harv-Fehler: kein Ziel: CITEREFAdams2001 ( Hilfe )

• Burde, Gerhard ; Zieschang, Heiner (1985), Knoten , De Gruyter Studium der Mathematik, 5 , Walter de Gruyter, ISBN 978-3-11-008675-1
• Crowell, Richard H .; Fox, Ralph (1977). Einführung in die Knotentheorie . ISBN 978-0-387-90272-2.
• Kauffman, Louis H. (1987), On Knots , ISBN 978-0-691-08435-0
• Kauffman, Louis H. (2013), Knoten und Physik (4. Aufl.), World Scientific, ISBN 978-981-4383-00-4

Umfragen

• Menasco, William W.; Thistlethwaite, Morwen , Hrsg. (2005), Handbuch der Knotentheorie , Elsevier, ISBN 978-0-444-51452-3
  • Das Handbuch von Menasco und Thistlethwaite untersucht eine Mischung von Themen, die für aktuelle Forschungstrends relevant sind, in einer Weise, die für fortgeschrittene Studenten zugänglich, aber für professionelle Forscher von Interesse ist.
• Livio, Mario (2009), "Kap. 8: Unangemessene Wirksamkeit?" , Ist Gott ein Mathematiker? , Simon & Schuster, S. 203–218, ISBN 978-0-7432-9405-8

Externe Links

• "Mathematik und Knoten" Dies ist eine Online-Version einer Ausstellung, die für die "PopMath RoadShow" der Royal Society 1989 entwickelt wurde. Ziel war es, mit Hilfe von Knoten Methoden der Mathematik einer breiten Öffentlichkeit vorzustellen.

Geschichte

• Thomson, Sir William (1867), "On Vortex Atoms" , Proceedings of the Royal Society of Edinburgh , VI : 94–105
• Silliman, Robert H. (Dezember 1963), "William Thomson: Smoke Rings and Nineteenth-Century Atomism", Isis , 54 (4): 461–474, doi : 10.1086/349764 , JSTOR  228151
• Film einer modernen Nachbildung von Taits Rauchringexperiment
• Geschichte der Knotentheorie (auf der Homepage von Andrew Ranicki )

Knotentabellen und Software

• KnotInfo : Tabelle der Knoteninvarianten und Ressourcen zur Knotentheorie
• Der Knotenatlas — detaillierte Informationen zu einzelnen Knoten in Knotentabellen
• KnotPlot — Software zur Untersuchung geometrischer Eigenschaften von Knoten
• Knotscape — Software zum Erstellen von Knotenbildern
• Knoutilus — Online-Datenbank und Bildgenerator von Knoten
• KnotData.html — Wolfram Mathematica Funktion zur Untersuchung von Knoten