Lorenz-System - Lorenz system

Eine Beispiellösung im Lorenz-Attraktor für ρ = 28, σ = 10 und β = 8/3

Das Lorenz-System ist ein System gewöhnlicher Differentialgleichungen, das zuerst von Edward Lorenz untersucht wurde . Es zeichnet sich durch chaotische Lösungen für bestimmte Parameterwerte und Anfangsbedingungen aus. Insbesondere ist der Lorenz-Attraktor eine Menge chaotischer Lösungen des Lorenz-Systems. In populären Medien stammt der " Schmetterlingseffekt " aus den realen Implikationen des Lorenz-Attraktors, dh in jedem physikalischen System, in Ermangelung perfekter Kenntnis der Anfangsbedingungen (sogar die winzige Störung der Luft durch einen Schmetterlingsflattern). seine Flügel) wird unsere Fähigkeit, seinen zukünftigen Kurs vorherzusagen, immer versagen. Dies unterstreicht, dass physikalische Systeme auch ohne Quanteneffekte vollständig deterministisch und dennoch von Natur aus unberechenbar sein können. Die Form des Lorenz-Attraktors selbst kann, wenn sie grafisch aufgetragen wird, auch einem Schmetterling ähneln.

Überblick

1963 entwickelte Edward Lorenz mit Hilfe von Ellen Fetter ein vereinfachtes mathematisches Modell für die atmosphärische Konvektion . Das Modell ist ein System von drei gewöhnlichen Differentialgleichungen, die heute als Lorenz-Gleichungen bekannt sind:

${\displaystyle {\begin{ausgerichtet}{\frac {\mathrm {d} x}{\mathrm {d} t}}&=\sigma (yx),\\[6pt]{\frac {\mathrm {d } y}{\mathrm {d} t}}&=x(\rho -z)-y,\\[6pt]{\frac {\mathrm {d} z}{\mathrm {d}t}}& =xy-\beta z.\end{ausgerichtet}}}$

Die Gleichungen beziehen sich auf die Eigenschaften einer zweidimensionalen Flüssigkeitsschicht, die von unten gleichmäßig erwärmt und von oben gekühlt wird. Insbesondere beschreiben die Gleichungen die Änderungsrate von drei Größen in Bezug auf die Zeit: ist proportional zur Konvektionsrate, zur horizontalen Temperaturänderung und zur vertikalen Temperaturänderung. Die Konstanten , , und sind Systemparameter, die proportional zur Prandtl-Zahl , Rayleigh-Zahl und bestimmten physikalischen Abmessungen der Schicht selbst sind. ${\displaystyle x}$${\displaystyle y}$${\displaystyle z}$${\displaystyle \sigma}$${\displaystyle \rho}$${\displaystyle \beta}$

Die Lorenz-Gleichungen treten auch in vereinfachten Modellen für Laser , Dynamos , Thermosiphons , bürstenlose Gleichstrommotoren , elektrische Schaltungen , chemische Reaktionen und Vorwärtsosmose auf . Die Lorenz-Gleichungen sind auch die maßgebenden Gleichungen im Fourier-Raum für das Malkus-Wasserrad . Das Malkus-Wasserrad zeigt eine chaotische Bewegung, bei der sich seine Drehung, anstatt sich mit konstanter Geschwindigkeit in eine Richtung zu drehen, beschleunigt, verlangsamt, stoppt, die Richtung ändert und auf unvorhersehbare Weise zwischen Kombinationen solcher Verhaltensweisen hin und her oszilliert.

Aus technischer Sicht ist das Lorenz-System nichtlinear , nichtperiodisch, dreidimensional und deterministisch . Die Lorenz-Gleichungen waren Gegenstand von Hunderten von Forschungsartikeln und mindestens einer Studie in Buchlänge.

Analyse

Normalerweise geht man davon aus, dass die Parameter , , und positiv sind. Lorenz verwendet , um die Werte , und . Das System zeigt bei diesen (und nahegelegenen) Werten ein chaotisches Verhalten. ${\displaystyle \sigma}$${\displaystyle \rho}$${\displaystyle \beta}$${\displaystyle \sigma =10}$${\displaystyle \beta =8/3}$${\displaystyle \rho =28}$

Wenn es dann nur einen Gleichgewichtspunkt gibt, der im Ursprung liegt. Dieser Punkt entspricht keiner Konvektion. Alle Bahnen konvergieren zum Ursprung, der ein globaler Attraktor ist , wenn . ${\displaystyle \rho <1}$${\displaystyle \rho <1}$

Eine Heugabelgabelung tritt bei auf , und zwei weitere kritische Punkte erscheinen bei: und Diese entsprechen einer stetigen Konvektion. Dieses Gleichgewichtspunktpaar ist nur dann stabil, wenn ${\displaystyle \rho=1}$${\displaystyle \rho >1}$${\displaystyle \left({\sqrt {\beta (\rho -1)}},{\sqrt {\beta (\rho -1)}},\rho -1\right)}$${\displaystyle \left(-{\sqrt {\beta (\rho -1)}}},-{\sqrt {\beta (\rho -1)}},\rho -1\right).}$

${\displaystyle \rho <\sigma {\frac {\sigma +\beta +3}{\sigma -\beta -1}},}$

die nur positiv gelten kann, wenn . Beim kritischen Wert verlieren beide Gleichgewichtspunkte durch eine unterkritische Hopf-Bifurkation an Stabilität . ${\displaystyle \rho}$${\displaystyle \sigma >\beta +1}$

Wenn , , und , hat das Lorenz-System chaotische Lösungen (aber nicht alle Lösungen sind chaotisch). Fast alle Anfangspunkte tendieren zu einer invarianten Menge – dem Lorenz-Attraktor – einem seltsamen Attraktor , einem Fraktal und einem selbsterregten Attraktor in Bezug auf alle drei Gleichgewichte. Seine Hausdorff-Dimension wird von oben durch die Lyapunov-Dimension (Kaplan-Yorke-Dimension) auf 2,06 ± 0,01 geschätzt , und die Korrelationsdimension wird auf 2,05 ± 0,01 geschätzt. Die exakte Lyapunov-Dimensionsformel des globalen Attraktors lässt sich analytisch unter klassischen Einschränkungen der Parameter ermitteln: ${\displaystyle \rho =28}$${\displaystyle \sigma =10}$${\displaystyle \beta =8/3}$${\displaystyle 3-{\frac {2(\sigma +\beta+1)}{\sigma +1+{\sqrt {(\sigma -1)^{2}+4\sigma\rho}}}} .}$

Der Lorenz-Attraktor ist schwer zu analysieren, aber die Wirkung der Differentialgleichung auf den Attraktor wird durch ein ziemlich einfaches geometrisches Modell beschrieben. Der Beweis, dass dies tatsächlich der Fall ist, ist das vierzehnte Problem auf der Liste der Probleme von Smale . Dieses Problem wurde 2002 von Warwick Tucker als erstes gelöst .

Für andere Werte von zeigt das System verknotete periodische Bahnen an. Damit wird zum Beispiel ein T (3,2) Torusknoten . ${\displaystyle \rho}$${\displaystyle \rho =99,96}$

Beispiellösungen des Lorenz-Systems für verschiedene Werte von ρ
ρ = 14, σ = 10, β = 8/3 (Vergrößern)	ρ = 13, σ = 10, β = 8/3 (Vergrößern)
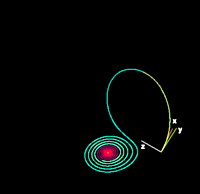
ρ = 15, σ = 10, β = 8/3 (Vergrößern)	ρ = 28, σ = 10, β = 8/3 (Vergrößern)
Für kleine Werte von ρ ist das System stabil und entwickelt sich zu einem von zwei Fixpunktattraktoren. Wenn ρ größer als 24,74 ist, werden die Fixpunkte zu Repulsoren und die Flugbahn wird von ihnen auf sehr komplexe Weise abgestoßen.

Sensible Abhängigkeit von der Anfangsbedingung
Zeit t = 1 (Vergrößern)	Zeit t = 2 (Vergrößern)	Zeit t = 3 (Vergrößern)
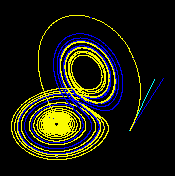
Diese Abbildungen – erstellt mit ρ = 28, σ = 10 und β = 8/3 – zeigen drei Zeitabschnitte der 3-D-Entwicklung zweier Trajektorien (eine in Blau, die andere in Gelb) im Lorenz-Attraktor beginnend bei zwei anfänglichen Punkte, die sich nur um 10 −5 in der x- Koordinate unterscheiden. Anfangs scheinen die beiden Trajektorien zusammenzufallen (nur die gelbe ist zu sehen, da sie über die blaue gezeichnet wird), aber nach einiger Zeit ist die Divergenz offensichtlich.

Verbindung zum Zeltplan

Eine Nachbildung der Ergebnisse von Lorenz, die auf Mathematica erstellt wurde . Punkte über der roten Linie entsprechen den Schaltkeulen des Systems.

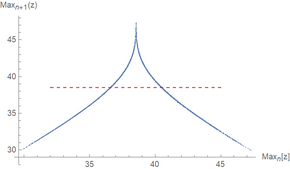
In Abbildung 4 seiner Arbeit hat Lorenz den vom System erreichten relativen Maximalwert in z-Richtung gegen den vorherigen relativen Maximalwert in z-Richtung aufgetragen. Dieses Verfahren wurde später als Lorenz-Karte bekannt (nicht zu verwechseln mit einem Poincaré-Plot , der die Schnittpunkte einer Trajektorie mit einer vorgegebenen Oberfläche darstellt). Das resultierende Grundstück hat eine Form, die der Zeltkarte sehr ähnlich ist . Lorenz fand auch heraus, dass das System auf die nächste Keule umschaltet, wenn der maximale z-Wert über einem bestimmten Grenzwert liegt. In Kombination mit dem bekannten Chaos der Zeltkarte zeigte er, dass das System chaotisch zwischen den beiden Lappen wechselt.

Simulationen

MATLAB-Simulation

% Solve over time interval [0,100] with initial conditions [1,1,1]
% ''f'' is set of differential equations
% ''a'' is array containing x, y, and z variables
% ''t'' is time variable

sigma = 10;
beta = 8/3;
rho = 28;
f = @(t,a) [-sigma*a(1) + sigma*a(2); rho*a(1) - a(2) - a(1)*a(3); -beta*a(3) + a(1)*a(2)];
[t,a] = ode45(f,[0 100],[1 1 1]);     % Runge-Kutta 4th/5th order ODE solver
plot3(a(:,1),a(:,2),a(:,3))

Mathematica-Simulation

Standardweg:

tend = 50;
eq = {x'[t] == σ (y[t] - x[t]), 
      y'[t] == x[t] (ρ - z[t]) - y[t], 
      z'[t] == x[t] y[t] - β z[t]};
init = {x[0] == 10, y[0] == 10, z[0] == 10};
pars = {σ->10, ρ->28, β->8/3};
{xs, ys, zs} = 
  NDSolveValue[{eq /. pars, init}, {x, y, z}, {t, 0, tend}];
ParametricPlot3D[{xs[t], ys[t], zs[t]}, {t, 0, tend}]

Weniger ausführlich:

lorenz = NonlinearStateSpaceModel[{{σ (y - x), x (ρ - z) - y, x y - β z}, {}}, {x, y, z}, {σ, ρ, β}];
soln[t_] = StateResponse[{lorenz, {10, 10, 10}}, {10, 28, 8/3}, {t, 0, 50}];
ParametricPlot3D[soln[t], {t, 0, 50}]

Python-Simulation

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
from mpl_toolkits.mplot3d import Axes3D

rho = 28.0
sigma = 10.0
beta = 8.0 / 3.0

def f(state, t):
    x, y, z = state  # Unpack the state vector
    return sigma * (y - x), x * (rho - z) - y, x * y - beta * z  # Derivatives

state0 = [1.0, 1.0, 1.0]
t = np.arange(0.0, 40.0, 0.01)

states = odeint(f, state0, t)

fig = plt.figure()
ax = fig.gca(projection="3d")
ax.plot(states[:, 0], states[:, 1], states[:, 2])
plt.draw()
plt.show()

Herleitung der Lorenz-Gleichungen als Modell für atmosphärische Konvektion

Die Lorenz-Gleichungen sind aus der Oberbeck-Boussinesq-Näherung der Gleichungen abgeleitet , die die Flüssigkeitszirkulation in einer flachen Flüssigkeitsschicht beschreiben, die von unten gleichmäßig erhitzt und von oben gleichmäßig gekühlt wird. Diese Flüssigkeitszirkulation wird als Rayleigh-Bénard-Konvektion bezeichnet . Es wird angenommen, dass die Flüssigkeit in zwei Dimensionen (vertikal und horizontal) mit periodischen rechteckigen Randbedingungen zirkuliert.

Die partiellen Differentialgleichungen, die die Strömungsfunktion und die Temperatur des Systems modellieren , werden einer spektralen Galerkin-Näherung unterzogen : Die hydrodynamischen Felder werden in Fourier-Reihen erweitert, die dann stark auf einen einzigen Term für die Strömungsfunktion und zwei Terme für die Temperatur verkürzt werden. Dies reduziert die Modellgleichungen auf einen Satz von drei gekoppelten, nichtlinearen gewöhnlichen Differentialgleichungen. Eine detaillierte Herleitung findet sich beispielsweise in nichtlinearen Dynamiktexten. Das Lorenz-System ist eine reduzierte Version eines größeren Systems, das zuvor von Barry Saltzman untersucht wurde.

Lösung von Smales 14. Problem

Smales 14. Problem lautet: „Haben die Eigenschaften des Lorenz-Attraktors die eines seltsamen Attraktors ?“, wurde 2002 von Warwick Tucker bejaht . Um dieses Ergebnis zu beweisen, verwendete Tucker rigorose numerische Methoden wie Intervallarithmetik und Normalformen . Zunächst definiert Tucker einen Querschnitt , der von den Strömungstrajektorien quer geschnitten wird. Daraus kann man die First-Return-Map definieren , die jedem den Punkt zuordnet, an dem sich die Trajektorie von First schneidet . ${\displaystyle \Sigma \subset \{x_{3}=r-1\}}$${\displaystyle P}$${\displaystyle x\in\Sigma}$${\displaystyle P(x)}$${\displaystyle x}$${\displaystyle \Sigma}$

Dann wird der Beweis in drei Hauptpunkte aufgeteilt, die bewiesen sind und die Existenz eines seltsamen Attraktors implizieren. Die drei Punkte sind:

• Unter der First-Return-Karte existiert eine Regionsinvariante, d. h${\displaystyle N\subset \Sigma}$${\displaystyle P(N)\Teilmenge N}$
• Die Rückkehrabbildung lässt ein vorwärtsinvariantes Kegelfeld zu
• Vektoren innerhalb dieses invarianten Kegelfeldes werden durch die Ableitung der Rückkehrabbildung gleichförmig erweitert .${\displaystyle DP}$

Um den ersten Punkt zu beweisen, bemerken wir, dass der Querschnitt von zwei Bögen geschnitten wird, die von (siehe ) gebildet werden. Tucker bedeckt die Lage dieser beiden Bögen durch kleine Rechtecke , die Vereinigung dieser Rechtecke ergibt . Das Ziel ist nun zu beweisen, dass für alle Punkte in , der Fluss die Punkte in , in zurückbringt . Um dies zu tun, nehmen wir einen Plan unten in einem Abstand klein ist , dann durch das Zentrum unter dem und Euler Integrationsverfahren verwendet wird , kann man sich ausrechnen , wo die Strömung bringt in denen gibt uns einen neuen Punkt . Dann kann man mit Hilfe der Taylor-Entwicklung abschätzen, wo die Punkte in abgebildet werden. Dies gibt uns ein neues Rechteck mit dem Mittelpunkt von . Somit wissen wir, dass alle Punkte in in abgebildet werden . Das Ziel ist , diese Methode rekursiv zu tun , bis der Ablauf zu zurückkommt und wir erhalten ein Rechteck in so dass wir wissen , dass . Das Problem ist, dass unsere Schätzung nach mehreren Iterationen ungenau werden kann, daher teilt Tucker in kleinere Rechtecke auf und wendet den Prozess dann rekursiv an. Ein weiteres Problem besteht darin, dass der Fluss bei der Anwendung dieses Algorithmus „horizontaler“ wird (siehe ), was zu einer dramatischen Zunahme der Ungenauigkeit führt. Um dies zu verhindern, ändert der Algorithmus die Ausrichtung der Querschnitte, sodass sie entweder horizontal oder vertikal werden. ${\displaystyle \Sigma}$${\displaystyle P(\Sigma)}$${\displaystyle R_{i}}$${\displaystyle N}$${\displaystyle N}$${\displaystyle \Sigma}$${\displaystyle N}$${\displaystyle \Sigma '}$${\displaystyle \Sigma}$${\displaystyle h}$${\displaystyle c_{i}}$${\displaystyle R_{i}}$${\displaystyle c_{i}}$${\displaystyle \Sigma '}$${\displaystyle c_{i}'}$${\displaystyle \Sigma}$${\displaystyle \Sigma '}$${\displaystyle R_{i}'}$${\displaystyle c_{i}}$${\displaystyle R_{i}}$${\displaystyle R_{i}'}$${\displaystyle \Sigma}$${\displaystyle Rf_{i}}$${\displaystyle \Sigma}$${\displaystyle P(R_{i})\subset Rf_{i}}$${\displaystyle R_{i}'}$${\displaystyle R_{i,j}}$

Beiträge

Lorenz würdigt die Beiträge von Ellen Fetter in seinem Beitrag, die für die numerischen Simulationen und Zahlen verantwortlich ist. Außerdem half Margaret Hamilton bei den ersten numerischen Berechnungen, die zu den Ergebnissen des Lorenz-Modells führten.

Galerie

• 

  Eine Lösung im Lorenz-Attraktor mit hoher Auflösung in der xz-Ebene aufgetragen.

• 

  Eine Lösung im Lorenz-Attraktor, gerendert als SVG.

• Medien abspielen

  Eine Animation, die Trajektorien mehrerer Lösungen in einem Lorenz-System zeigt.

• 

  Eine Lösung im Lorenz-Attraktor, gerendert als Metalldraht, um Richtung und 3D- Struktur anzuzeigen .

• Medien abspielen

  Eine Animation, die die Divergenz nahegelegener Lösungen zum Lorenz-System zeigt.

• 

  Eine Visualisierung des Lorenz-Attraktors in der Nähe eines intermittierenden Zyklus.

• 

  Zwei Stromlinien in einem Lorenz-System, von rho=0 bis rho=28 (sigma=10, beta=8/3)

• 

  Animation eines Lorenz-Systems mit Rho-Abhängigkeit

Siehe auch

• Edens Vermutung zur Lyapunov-Dimension
• Lorenz 96-Modell
• Liste der chaotischen Karten
• Takens-Theorem

Anmerkungen

Verweise

• Bergé, Pierre; Pomeau, Yves; Vidal, Christian (1984). Ordnung im Chaos: Auf dem Weg zu einem deterministischen Ansatz für Turbulenzen . New York: John Wiley & Söhne . ISBN 978-0-471-84967-4.
• Cuomo, Kevin M.; Oppenheim, Alan V. (1993). "Schaltungsimplementierung von synchronisiertem Chaos mit Anwendungen zur Kommunikation". Physische Überprüfungsbriefe . 71 (1): 65–68. Bibcode : 1993PhRvL..71...65C . doi : 10.1103/PhysRevLett.71.65 . ISSN  0031-9007 . PMID  10054374 .
• Gorman, M.; Widmann, PJ; Robbins, KA (1986). „Nichtlineare Dynamik einer Konvektionsschleife: Ein quantitativer Vergleich des Experiments mit der Theorie“. Physica D . 19 (2): 255–267. Bibcode : 1986PhyD...19..255G . doi : 10.1016/0167-2789(86)90022-9 .
• Grassberger, P.; Procaccia, I. (1983). „Messung der Fremdheit von seltsamen Attraktoren“. Physica D . 9 (1–2): 189–208. Bibcode : 1983PhyD....9..189G . doi : 10.1016/0167-2789(83)90298-1 .
• Haken, H. (1975). „Analogie zwischen höheren Instabilitäten in Flüssigkeiten und Lasern“. Physik Buchstaben A . 53 (1): 77–78. Bibcode : 1975PhLA...53...77H . doi : 10.1016/0375-9601(75)90353-9 .
• Hemati, N. (1994). „Seltsame Attraktoren in bürstenlosen Gleichstrommotoren“. IEEE Transactions on Circuits and Systems I: Grundlegende Theorie und Anwendungen . 41 (1): 40–45. doi : 10.1109/81.260218 . ISSN  1057-7122 .
• Hilborn, Robert C. (2000). Chaos und nichtlineare Dynamik: Eine Einführung für Wissenschaftler und Ingenieure (zweite Aufl.). Oxford University Press . ISBN 978-0-19-850723-9.
• Hirsch, Morris W. ; Klein, Stephen ; Devaney, Robert (2003). Differentialgleichungen, dynamische Systeme und eine Einführung in das Chaos (zweite Aufl.). Boston, MA: Akademische Presse . ISBN 978-0-12-349703-1.
• Knobloch, Edgar (1981). „Chaos im segmentierten Scheibendynamo“. Physik Buchstaben A . 82 (9): 439–440. Bibcode : 1981PhLA...82..439K . doi : 10.1016/0375-9601(81)90274-7 .
• Kolář, Miroslav; Gumbs, Godfrey (1992). „Theorie zur experimentellen Beobachtung von Chaos in einem rotierenden Wasserrad“. Physical Review A . 45 (2): 626–637. doi : 10.1103/PhysRevA.45.626 . PMID  9907027 .
• Leonov, GA; Kuznetsov, NV; Korzhemanova, NA; Kusakin, DV (2016). „Lyapunov-Dimensionsformel für den globalen Attraktor des Lorenz-Systems“. Kommunikation in der nichtlinearen Wissenschaft und numerischen Simulation . 41 : 84–103. arXiv : 1508.07498 . Bibcode : 2016CNSNS..41...84L . doi : 10.1016/j.cnsns.2016.04.032 .
• Lorenz, Edward Norton (1963). "Deterministischer nichtperiodischer Fluss" . Zeitschrift der Atmosphärenwissenschaften . 20 (2): 130–141. Bibcode : 1963JAtS...20..130L . doi : 10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2 .
• Mishra, Aashwin; Sanghi, Sanjeev (2006). „Eine Studie über das asymmetrische Malkus-Wasserrad: Die voreingenommenen Lorenz-Gleichungen“. Chaos: Eine interdisziplinäre Zeitschrift für nichtlineare Wissenschaft . 16 (1): 013114. Bibcode : 2006Chaos..16a3114M . doi : 10.1063/1.2154792 . PMID  16599745 .
• Pchelintsev, AN (2014). „Numerische und physikalische Modellierung der Dynamik des Lorenz-Systems“. Numerische Analyse und Anwendungen . 7 (2): 159–167. doi : 10.1134/S1995423914020098 .
• Polen, Douglas (1993). „Kooperative Katalyse und chemisches Chaos: ein chemisches Modell für die Lorenz-Gleichungen“. Physica D . 65 (1): 86–99. Bibcode : 1993PhyD...65...86P . doi : 10.1016/0167-2789(93)90006-M .
• Saltzman, Barry (1962). "Freie Konvektion mit endlicher Amplitude als Anfangswertproblem - I" . Zeitschrift der Atmosphärenwissenschaften . 19 (4): 329–341. Bibcode : 1962JAtS...19..329S . doi : 10.1175/1520-0469(1962)019<0329:FAFCAA>2.0.CO;2 .
• Sparrow, Colin (1982). Die Lorenz-Gleichungen: Bifurkationen, Chaos und seltsame Attraktoren . Springer.
• Tucker, Warwick (2002). "Ein rigoroser ODE-Löser und das 14. Problem von Smale" (PDF) . Grundlagen der Computermathematik . 2 (1): 53–117. CiteSeerX  10.1.1.545.3996 . doi : 10.1007/s002080010018 .
• Tzenov, Stephan (2014). „Seltsame Attraktoren, die die osmotische Instabilität charakterisieren“. arXiv : 1406.0979v1 [ physik.flu-dyn ].
• Viana, Marcelo (2000). "Was ist neu an Lorenz seltsamen Attraktoren?". Der Mathematische Intelligenz . 22 (3): 6–19. doi : 10.1007/BF03025276 .
• Lorenz, Edward N. (1960). "Die statistische Vorhersage von Lösungen dynamischer Gleichungen" (PDF) . Symposium zur numerischen Wettervorhersage in Tokio .

Weiterlesen

• GA Leonov & NV Kuznetsov (2015). "Über Unterschiede und Gemeinsamkeiten in der Analyse von Lorenz-, Chen- und Lu-Systemen" (PDF) . Angewandte Mathematik und Informatik . 256 : 334–343. doi : 10.1016/j.amc.2014.12.132 .

Externe Links

• "Lorenz-Attraktor" , Enzyklopädie der Mathematik , EMS Press , 2001 [1994]
• Weisstein, Eric W. "Lorenz-Attraktor" . MathWorld .
• Lorenz Attraktor von Rob Morris, Wolfram Demonstrations Project .
• Lorenz-Gleichung auf planetmath.org
• Synchronisiertes Chaos und private Kommunikation mit Kevin Cuomo . Die Implementierung des Lorenz-Attraktors in eine elektronische Schaltung.
• Lorenz Attraktor interaktive Animation (Sie benötigen das Adobe Shockwave Plugin)
• 3D-Attraktoren: Mac-Programm zum Visualisieren und Erkunden des Lorenz-Attraktors in 3 Dimensionen
• Lorenz Attractor in analoger Elektronik implementiert
• Lorenz Attractor interaktive Animation (implementiert in Ada mit GTK+. Quellen & ausführbar)
• Webbasierter Lorenz Attractor (implementiert in JavaScript/HTML/CSS)
• Interaktiver webbasierter Lorenz Attractor mit Iodide