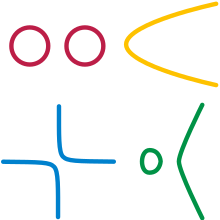Verteiler - Manifold

In der Mathematik ist eine Mannigfaltigkeit ein topologischer Raum , der in der Nähe jedes Punktes lokal dem euklidischen Raum ähnelt . Mehr eine präzise, n -dimensionalen Verteiler oder n Mannigfaltigkeit kurz, ist ein topologischer Raum mit der Eigenschaft , dass jeder Punkt A Nachbarschaft , die ist homeomorphic in eine offene Teilmenge von n - dimensionalen euklidischen Raum.
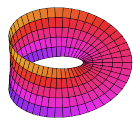
Eindimensionale Mannigfaltigkeiten umfassen Linien und Kreise , aber keine Achter . Zweidimensionale Mannigfaltigkeiten werden auch Flächen genannt . Beispiele sind die Ebene , die Kugel und der Torus , aber auch die Klein-Flasche und die reale projektive Ebene .
Der Begriff einer Mannigfaltigkeit ist für viele Teile der Geometrie und der modernen mathematischen Physik von zentraler Bedeutung, da er es ermöglicht, komplizierte Strukturen durch gut verstandene topologische Eigenschaften einfacherer Räume zu beschreiben. Mannigfaltigkeiten entstehen natürlicherweise als Lösungsmengen von Gleichungssystemen und als Graphen von Funktionen. Das Konzept findet Anwendung in Computergrafik und Augmented-Reality, da Bilder mit Koordinaten (zB CT-Scans) verknüpft werden müssen.
Verteiler können mit zusätzlicher Struktur ausgestattet werden. Eine wichtige Klasse von Mannigfaltigkeiten sind differenzierbare Mannigfaltigkeiten ; ihre differenzierbare Struktur ermöglicht Berechnungen . Eine Riemannsche Metrik auf einer Mannigfaltigkeit ermöglicht die Messung von Abständen und Winkeln . Symplektische Mannigfaltigkeiten dienen als Phasenräume im Hamiltonschen Formalismus der klassischen Mechanik , während vierdimensionale Lorentzsche Mannigfaltigkeiten die Raumzeit in der Allgemeinen Relativitätstheorie modellieren .
Das Studium von Mannigfaltigkeiten erfordert praktische Kenntnisse in Analysis und Topologie .
Motivierende Beispiele
Kreis
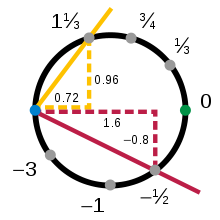
Nach einer Geraden ist der Kreis das einfachste Beispiel einer topologischen Mannigfaltigkeit. Die Topologie ignoriert die Biegung, sodass ein kleines Kreisstück genauso behandelt wird wie ein kleines Stück einer Linie. Betrachten wir zum Beispiel den oberen Teil des Einheitskreises , x 2 + y 2 = 1, wobei die y- Koordinate positiv ist (angezeigt durch den gelben Bogen in Abbildung 1 ). Jeder Punkt dieses Bogens kann eindeutig durch seine x -Koordinate beschrieben werden. So Projektion auf dem ersten Koordinate ist ein kontinuierliches und umkehrbar , Mapping von dem oberen Bogen zu dem offenen Intervall (-1, 1):
Solche Funktionen zusammen mit den offenen Regionen, die sie abbilden, werden als Diagramme bezeichnet . Ebenso gibt es Diagramme für den unteren (roten), linken (blauen) und rechten (grünen) Teil des Kreises:
Zusammen decken diese Teile den gesamten Kreis ab, und die vier Diagramme bilden einen Atlas für den Kreis.
Die oberen und rechten Diagramme, und jeweils überschneiden sich in ihrer Domäne: ihre Kreuzung liegt im Viertel des Kreises , wo beide und -Koordinaten positiv sind. Jeder ordnet diesen Teil dem Intervall zu , wenn auch anders. Auf diese Weise kann eine Funktion konstruiert werden, die Werte aus dem Co-Bereich von zurück zum Kreis mit der Umkehrung, gefolgt von zurück zum Intervall , konstruiert . Für eine beliebige Zahl a in gilt dann:
Eine solche Funktion wird als Übergangsabbildung bezeichnet .
Die oberen, unteren, linken und rechten Diagramme bilden nicht den einzig möglichen Atlas. Diagramme müssen keine geometrischen Projektionen sein, und die Anzahl der Diagramme ist frei wählbar. Betrachten Sie die Diagramme
Hier ist s die Steigung der Geraden durch den Punkt bei den Koordinaten ( x , y ) und den festen Drehpunkt (-1, 0); in ähnlicher Weise ist t das Gegenteil der Steigung der Linie durch die Punkte an den Koordinaten ( x , y ) und (+1, 0). Die inverse Abbildung von s nach ( x , y ) ist gegeben durch
Es kann bestätigt werden, dass x 2 + y 2 = 1 für alle Werte von s und t ist . Diese beiden Diagramme bieten einen zweiten Atlas für den Kreis mit der Übergangskarte
Jedes Diagramm lässt einen einzelnen Punkt weg, entweder (−1, 0) für s oder (+1, 0) für t , sodass kein Diagramm allein ausreicht, um den ganzen Kreis abzudecken. Es kann bewiesen werden, dass es nicht möglich ist, den vollen Kreis mit einem einzigen Diagramm abzudecken. Obwohl es beispielsweise möglich ist, einen Kreis aus einem einzelnen Linienintervall zu konstruieren, indem die Enden überlappt und "geklebt" werden, erzeugt dies kein Diagramm; ein Teil des Kreises wird auf beide Enden gleichzeitig abgebildet, wodurch die Invertibilität verloren geht.
Kugel
Die Kugel ist ein Beispiel für eine Oberfläche. Die Einheitssphäre der impliziten Gleichung
- x 2 + y 2 + z 2 – 1 = 0
kann von einem Atlas von sechs Karten abgedeckt werden : die Ebene z = 0 teilt die Kugel in zwei Halbkugeln ( z > 0 und z < 0 ), die beide durch die Projektion auf die Scheibe x 2 + y 2 < 1 abgebildet werden können auf der xy- Koordinatenebene. Dies bietet zwei Diagramme; die vier anderen Karten werden durch eine ähnliche Konstruktion mit den beiden anderen Koordinatenebenen bereitgestellt.
Für den Kreis kann man ein Diagramm definieren, das die gesamte Kugel mit Ausnahme eines Punktes abdeckt. Somit sind zwei Karten ausreichend, aber die Kugel kann nicht von einer einzigen Karte abgedeckt werden.
Dieses Beispiel ist historisch bedeutsam, da es die Terminologie motiviert hat; es zeigte sich , dass die gesamte Oberfläche der Erde nicht eine ebene Darstellung , bestehend aus einer einzelnen haben kann Karte (auch „Plan“ genannt, siehe Seekarte ) und daher ein Bedarf Atlanten zur Abdeckung der gesamten Erdoberfläche.
Andere Kurven
Verteiler müssen nicht verbunden werden (alles in "einem Stück"); ein Beispiel ist ein Paar separater Kreise.
Verteiler müssen nicht geschlossen werden ; somit ist ein Liniensegment ohne seine Endpunkte eine Mannigfaltigkeit. Sie sind niemals abzählbar , es sei denn, die Dimension der Mannigfaltigkeit ist 0. Wenn man diese Freiheiten zusammenfasst, sind andere Beispiele für Mannigfaltigkeiten eine Parabel , eine Hyperbel und der Ort von Punkten auf einer kubischen Kurve y 2 = x 3 − x (eine geschlossene Schleife Stück und ein offenes, unendliches Stück).
Ausgeschlossen sind jedoch Beispiele wie zwei sich berührende Kreise, die sich einen Punkt teilen, um eine Acht zu bilden; am gemeinsamen Punkt kann kein zufriedenstellendes Diagramm erstellt werden. Selbst bei der durch die Topologie zulässigen Biegung sieht die Umgebung des gemeinsamen Punkts wie ein "+" aus, nicht wie eine Linie. Ein "+" ist nicht homöomorph zu einem Liniensegment, da das Entfernen des Mittelpunkts aus dem "+" einen Raum mit vier Komponenten (dh Stücken) ergibt, während das Entfernen eines Punkts aus einem Liniensegment einen Raum mit höchstens zwei Stücken ergibt; topologische Operationen erhalten immer die Stückzahl.
Mathematische Definition
Informell ist eine Mannigfaltigkeit ein Raum , der dem euklidischen Raum "nachgebildet" ist.
Es gibt viele verschiedene Arten von Verteilern. In Geometrie und Topologie sind alle Mannigfaltigkeiten topologische Mannigfaltigkeiten , möglicherweise mit zusätzlicher Struktur. Eine Mannigfaltigkeit kann konstruiert werden, indem man eine Sammlung von Koordinatentafeln angibt, d. h. eine Überdeckung durch offene Mengen mit Homöomorphismen auf einen euklidischen Raum und Patchfunktionen: Homöomorphismen von einer Region des euklidischen Raums in eine andere Region, wenn sie dem gleichen Teil von entsprechen die Mannigfaltigkeit in zwei verschiedenen Koordinatendiagrammen. Einer Mannigfaltigkeit kann eine zusätzliche Struktur gegeben werden, wenn die Patching-Funktionen Axiome jenseits der Stetigkeit erfüllen. Zum Beispiel haben differenzierbare Mannigfaltigkeiten Homöomorphismen auf überlappenden Umgebungen, die zueinander diffeomorph sind, so dass die Mannigfaltigkeit einen wohldefinierten Satz von Funktionen hat, die in jeder Umgebung differenzierbar sind, also auf die Mannigfaltigkeit als Ganzes differenzierbar sind.
Formal ist eine (topologische) Mannigfaltigkeit ein zweiter abzählbarer Hausdorff-Raum , der lokal homöomorph zum euklidischen Raum ist.
Zweitzählbar und Hausdorff sind Punktmengenbedingungen ; zweite Abzählbar schließt Räume aus, die in gewissem Sinne 'zu groß' sind, wie die lange Linie , während Hausdorff Räume wie "die Linie mit zwei Ursprüngen" ausschließt (diese Verallgemeinerungen von Mannigfaltigkeiten werden in Nicht-Hausdorff-Mannigfaltigkeiten diskutiert ).
Lokal homöomorph zum euklidischen Raum bedeutet, dass jeder Punkt eine zu einer offenen euklidischen n- Kugel homöomorphe Nachbarschaft hat ,
Allgemein wird angenommen, dass Mannigfaltigkeiten eine feste Dimension haben (der Raum muss lokal homöomorph zu einer festen n- Kugel sein), und ein solcher Raum wird n- Mannigfaltigkeit genannt ; einige Autoren lassen jedoch Mannigfaltigkeiten zu, bei denen verschiedene Punkte unterschiedliche Dimensionen haben können . Hat eine Mannigfaltigkeit eine feste Dimension, heißt sie reine Mannigfaltigkeit . Zum Beispiel hat die (Oberfläche einer) Kugel eine konstante Dimension von 2 und ist daher eine reine Mannigfaltigkeit, während die disjunkte Vereinigung einer Kugel und einer Linie im dreidimensionalen Raum keine reine Mannigfaltigkeit ist. Da die Dimension eine lokale Invariante ist (dh die Karte, die jeden Punkt an die Dimension ihrer Nachbarschaft sendet, über die ein Diagramm definiert ist, ist lokal konstant ), hat jede verbundene Komponente eine feste Dimension.
Schematheoretisch ist eine Mannigfaltigkeit ein lokal beringter Raum , dessen Strukturgarbe lokal isomorph zu der Garbe stetiger (oder differenzierbarer oder komplexanalytischer usw.) Funktionen auf dem euklidischen Raum ist. Diese Definition wird meistens verwendet, wenn analytische Mannigfaltigkeiten in der algebraischen Geometrie diskutiert werden .
Karten, Atlanten und Übergangskarten
Die kugelförmige Erde wird mit flachen Karten oder Diagrammen navigiert, die in einem Atlas gesammelt sind. In ähnlicher Weise kann eine differenzierbare Mannigfaltigkeit mit mathematischen Karten beschrieben werden , die als Koordinatendiagramme bezeichnet werden und in einem mathematischen Atlas gesammelt werden . Generell ist es nicht möglich, eine Mannigfaltigkeit mit nur einem Diagramm zu beschreiben, da sich die globale Struktur der Mannigfaltigkeit von der einfachen Struktur der Diagramme unterscheidet. Beispielsweise kann keine einzelne flache Karte die gesamte Erde darstellen, ohne dass benachbarte Features über die Kartengrenzen hinweg getrennt werden oder die Abdeckung dupliziert wird. Wenn eine Mannigfaltigkeit aus mehreren überlappenden Diagrammen erstellt wird, enthalten die Regionen, in denen sie sich überlappen, Informationen, die für das Verständnis der globalen Struktur unerlässlich sind.
Diagramme
Eine Koordinatenkarte , eine Koordinatenkarte oder einfach eine Karte einer Mannigfaltigkeit ist eine umkehrbare Karte zwischen einer Teilmenge der Mannigfaltigkeit und einem einfachen Raum, so dass sowohl die Karte als auch ihre Umkehrung die gewünschte Struktur beibehalten. Für eine topologische Mannigfaltigkeit ist der einfache Raum eine Teilmenge eines euklidischen Raums und das Interesse konzentriert sich auf die topologische Struktur. Diese Struktur wird durch
Homöomorphismen bewahrt , invertierbare Abbildungen, die in beide Richtungen stetig sind.Im Fall einer differenzierbaren Mannigfaltigkeit ermöglicht uns ein Satz von Diagrammen , der Atlas genannt wird, Berechnungen über Mannigfaltigkeiten. Polarkoordinaten bilden beispielsweise ein Diagramm für die Ebene abzüglich der positiven
x- Achse und des Ursprungs. Ein weiteres Beispiel für ein Diagramm ist die oben erwähnte Karte χ oben, ein Diagramm für den Kreis.Atlanten
Die Beschreibung der meisten Mannigfaltigkeiten erfordert mehr als ein Diagramm. Eine bestimmte Sammlung von Diagrammen, die eine Mannigfaltigkeit abdeckt, wird Atlas genannt . Ein Atlas ist nicht einzigartig, da alle Mannigfaltigkeiten auf verschiedene Weise mit verschiedenen Kombinationen von Diagrammen abgedeckt werden können. Zwei Atlanten werden als gleichwertig bezeichnet, wenn ihre Vereinigung ebenfalls ein Atlas ist.
Der Atlas, der alle möglichen Diagramme enthält, die mit einem gegebenen Atlas übereinstimmen, wird als maximaler Atlas bezeichnet (dh eine Äquivalenzklasse, die diesen gegebenen Atlas enthält). Im Gegensatz zu einem gewöhnlichen Atlas ist der maximale Atlas einer gegebenen Mannigfaltigkeit eindeutig. Obwohl es für Definitionen nützlich ist, ist es ein abstraktes Objekt und wird nicht direkt verwendet (zB in Berechnungen).
Übergangskarten
Karten in einem Atlas können sich überschneiden und ein einzelner Punkt einer Mannigfaltigkeit kann in mehreren Karten dargestellt werden. Wenn sich zwei Karten überschneiden, repräsentieren Teile von ihnen dieselbe Region der Mannigfaltigkeit, so wie eine Karte von Europa und eine Karte von Asien beide Moskau enthalten können. Bei zwei überlappenden Diagrammen kann eine Übergangsfunktion definiert werden, die von einer offenen Kugel in die Mannigfaltigkeit und dann zurück zu einer anderen (oder vielleicht gleichen) offenen Kugel in geht . Die resultierende Karte wird, wie die Karte
T im obigen Kreisbeispiel, als Koordinatenänderung , Koordinatentransformation , Übergangsfunktion oder Übergangskarte bezeichnet .Zusätzliche Struktur
Ein Atlas kann auch verwendet werden, um zusätzliche Strukturen auf dem Verteiler zu definieren. Die Struktur wird zunächst auf jedem Diagramm separat definiert. Wenn alle Übergangsabbildungen mit dieser Struktur kompatibel sind, wird die Struktur auf die Mannigfaltigkeit übertragen.
Dies ist die Standardmethode, mit der differenzierbare Mannigfaltigkeiten definiert werden. Bewahren die Übergangsfunktionen eines Atlas für eine topologische Mannigfaltigkeit die natürliche Differentialstruktur von (
dh sind sie Diffeomorphismen ), überträgt sich die Differentialstruktur auf die Mannigfaltigkeit und macht sie zu einer differenzierbaren Mannigfaltigkeit. Komplexe Mannigfaltigkeiten werden in analoger Weise eingeführt, indem gefordert wird, dass die Übergangsfunktionen eines Atlas holomorphe Funktionen sind . Für symplektische Mannigfaltigkeiten müssen die Übergangsfunktionen Symlektomorphismen sein .Die Struktur der Mannigfaltigkeit hängt vom Atlas ab, aber manchmal kann man sagen, dass verschiedene Atlanten dieselbe Struktur ergeben. Solche Atlanten werden als kompatibel bezeichnet .
Diese Begriffe werden im Allgemeinen durch die Verwendung von Pseudogruppen präzisiert .
Verteiler mit Begrenzung
Eine Mannigfaltigkeit mit Rand ist eine Mannigfaltigkeit mit einer Kante. Ein Blatt Papier ist beispielsweise eine 2-Mannigfaltigkeit mit einer 1-dimensionalen Grenze. Der Rand einer n -Mannigfaltigkeit mit Rand ist eine ( n −1) -Mannigfaltigkeit. Eine Scheibe (Kreis plus Inneres) ist eine 2-Mannigfaltigkeit mit Rand. Seine Grenze ist ein Kreis, eine 1-Mannigfaltigkeit . Ein Quadrat mit Innen ist auch eine 2-Mannigfaltigkeit mit Begrenzung. Eine Kugel (Kugel plus Innenraum) ist eine 3-Mannigfaltigkeit mit Rand. Seine Grenze ist eine Kugel, eine 2-Mannigfaltigkeit. (Siehe auch Begrenzung (Topologie) ).
In der Fachsprache ist eine Mannigfaltigkeit mit Rand ein Raum, der sowohl innere Punkte als auch Randpunkte enthält. Jeder innere Punkt hat eine zur offenen n- Kugel homöomorphe Umgebung {( x 1 , x 2 , ..., x n ) | Σ x i 2 < 1}. Jeder Randpunkt hat eine zur "halben" n -Kugel homöomorphe Umgebung {( x 1 , x 2 , ..., x n ) | Σ x i 2 < 1 und x 1 ≥ 0} . Der Homöomorphismus muss jeden Randpunkt zu einem Punkt mit x 1 = 0 schicken .
Grenze und Innenraum
Sei M eine Mannigfaltigkeit mit Rand. Das Innere von M , mit Int M bezeichnet , ist die Menge von Punkten in M, deren Umgebungen homöomorph zu einer offenen Teilmenge von sind . Die
Grenze von M , bezeichnet als ∂ M , ist das Komplement von Int M in M . Die Begrenzungspunkte können als jene Punkte , die Flächen auf der Grenzhyperebene charakterisiert werden ( x n = 0) von einigen Koordinate unter Diagramm.Ist M eine Mannigfaltigkeit mit Rand der Dimension n , dann ist Int
M eine Mannigfaltigkeit (ohne Rand) der Dimension n und ∂ M ist eine Mannigfaltigkeit (ohne Rand) der Dimension n − 1 .Konstruktion
Ein einzelner Verteiler kann auf unterschiedliche Weise konstruiert werden, wobei jede einen anderen Aspekt des Verteilers betont, was zu einem etwas anderen Standpunkt führt.
Diagramme
Der vielleicht einfachste Weg, eine Mannigfaltigkeit zu konstruieren, ist der, der im obigen Beispiel des Kreises verwendet wird. Zuerst wird eine Teilmenge von identifiziert, und dann wird ein Atlas erstellt, der diese Teilmenge abdeckt. Aus
solchen Konstruktionen ist der Mannigfaltigkeitsbegriff historisch gewachsen. Hier ist ein weiteres Beispiel für die Anwendung dieser Methode auf die Konstruktion einer Kugel:Kugel mit Diagrammen
Eine Kugel kann fast genauso behandelt werden wie ein Kreis. In der Mathematik ist eine Kugel nur die Oberfläche (nicht das feste Innere), die als Teilmenge von definiert werden kann :
Die Kugel ist zweidimensional, sodass jedes Diagramm einen Teil der Kugel einer offenen Untermenge von . Betrachten Sie die Nordhalbkugel, das ist der Teil mit positiver
z- Koordinate (im Bild rechts rot eingefärbt). Die Funktion χ definiert durchbildet die Nordhalbkugel auf die offene Einheitsscheibe ab, indem sie auf die ( x , y )-Ebene projiziert wird . Ein ähnliches Diagramm existiert für die Südhalbkugel. Zusammen mit zwei auf die ( x , z )-Ebene projizierten Karten und zwei auf die ( y , z )-Ebene projizierten Karten ergibt sich ein Atlas von sechs Karten, der die gesamte Kugel abdeckt.
Dies lässt sich leicht auf höherdimensionale Sphären verallgemeinern.
Patchwork
Eine Mannigfaltigkeit kann konstruiert werden, indem man Teile auf konsistente Weise zusammenfügt und sie zu überlappenden Diagrammen macht. Diese Konstruktion ist für jede Mannigfaltigkeit möglich und wird daher oft zur Charakterisierung verwendet, insbesondere für differenzierbare und Riemannsche Mannigfaltigkeiten. Es konzentriert sich auf einen Atlas, da die Patches natürlich Karten liefern, und da es keinen Außenraum gibt, führt es zu einer intrinsischen Sicht auf die Mannigfaltigkeit.
Die Mannigfaltigkeit wird konstruiert, indem ein Atlas angegeben wird, der selbst durch Übergangskarten definiert ist. Ein Punkt der Mannigfaltigkeit ist also eine Äquivalenzklasse von Punkten, die durch Übergangsabbildungen aufeinander abgebildet werden. Diagramme ordnen Äquivalenzklassen Punkten eines einzelnen Patches zu. An die Konsistenz der Übergangskarten werden in der Regel hohe Anforderungen gestellt. Für topologische Mannigfaltigkeiten müssen sie Homöomorphismen sein; wenn sie auch Diffeomorphismen sind, ist die resultierende Mannigfaltigkeit eine differenzierbare Mannigfaltigkeit.
Dies lässt sich mit der Übergangsabbildung t = 1 ⁄ s aus dem zweiten Halbkreisbeispiel veranschaulichen . Beginnen Sie mit zwei Kopien der Zeile. Verwenden Sie die Koordinaten s für die erste Kopie und t für die zweite Kopie. Kleben Sie nun beide Kopien zusammen, indem Sie den Punkt t auf der zweiten Kopie mit dem Punkt s = 1 ⁄ t auf der ersten Kopie identifizieren (die Punkte t = 0 und s = 0 werden mit keinem Punkt auf der ersten und zweiten Kopie identifiziert, bzw). Dies ergibt einen Kreis.
Intrinsische und extrinsische Sicht
Die erste Konstruktion und diese Konstruktion sind sehr ähnlich, repräsentieren aber ziemlich unterschiedliche Standpunkte. In der ersten Konstruktion sieht man die Mannigfaltigkeit als eingebettet in einen euklidischen Raum. Dies ist die extrinsische Sicht . Wenn man eine Mannigfaltigkeit auf diese Weise betrachtet, ist es leicht, die Intuition aus euklidischen Räumen zu verwenden, um zusätzliche Strukturen zu definieren. In einem euklidischen Raum ist es beispielsweise immer klar, ob ein Vektor an einem Punkt tangential oder senkrecht zu einer Oberfläche durch diesen Punkt verläuft.
Die Patchwork-Konstruktion verwendet keine Einbettung, sondern betrachtet die Mannigfaltigkeit lediglich als einen topologischen Raum für sich. Diese abstrakte Sicht wird als intrinsische Sicht bezeichnet . Es kann es schwieriger machen, sich vorzustellen, was ein Tangentenvektor sein könnte, und es gibt keinen intrinsischen Begriff eines Normalenbündels, sondern stattdessen ein intrinsisches stabiles Normalenbündel .
n -Kugel als Patchwork
Die n- Kugel S n ist eine Verallgemeinerung der Idee eines Kreises (1-Kugel) und Kugel (2-Kugel) auf höhere Dimensionen. Eine n- Kugel S n kann konstruiert werden, indem zwei Kopien von zusammengeklebt werden . Die Übergangskarte zwischen ihnen ist die
Inversion in einer Kugel , definiert alsDiese Funktion ist eine eigene Umkehrfunktion und kann somit in beide Richtungen verwendet werden. Da die Übergangsabbildung eine glatte Funktion ist , definiert dieser Atlas eine glatte Mannigfaltigkeit. Im Fall n = 1 vereinfacht sich das Beispiel zu dem oben gegebenen Kreisbeispiel.
Identifizieren von Punkten einer Mannigfaltigkeit
Es ist möglich, verschiedene Punkte einer Mannigfaltigkeit als gleich zu definieren. Dies kann man sich vorstellen, indem man diese Punkte zu einem einzigen Punkt zusammenfügt und so einen Quotientenraum bildet . Es gibt jedoch keinen Grund zu erwarten, dass solche Quotientenräume Mannigfaltigkeiten sind. Unter den möglichen Quotientenräumen, die nicht unbedingt Mannigfaltigkeiten sind, gelten Orbifolds und CW-Komplexe als relativ gutmütig . Ein Beispiel für einen Quotientenraum einer Mannigfaltigkeit, die auch eine Mannigfaltigkeit ist, ist der reale projektive Raum , der als Quotientenraum der entsprechenden Kugel identifiziert wird.
Eine Methode zum Identifizieren von Punkten (Zusammenkleben) ist die rechte (oder linke) Aktion einer Gruppe , die auf die Mannigfaltigkeit einwirkt . Zwei Punkte werden identifiziert, wenn einer von einem Gruppenelement auf den anderen verschoben wird. Wenn M die Mannigfaltigkeit und G die Gruppe ist, wird der resultierende Quotientenraum mit M / G (oder G \ M ) bezeichnet.
Mannigfaltigkeiten, die durch Identifizieren von Punkten konstruiert werden können, umfassen Tori und reelle projektive Räume (beginnend mit einer Ebene bzw. einer Kugel).
Entlang von Grenzen kleben
Zwei Mannigfaltigkeiten mit Begrenzungen können entlang einer Begrenzung zusammengeklebt werden. Wenn dies richtig gemacht wird, ist das Ergebnis auch eine Mannigfaltigkeit. Ebenso können zwei Begrenzungen einer einzelnen Mannigfaltigkeit zusammengeklebt werden.
Formal wird die Verklebung durch eine Bijektion zwischen den beiden Begrenzungen definiert. Zwei Punkte werden identifiziert, wenn sie aufeinander abgebildet werden. Für eine topologische Mannigfaltigkeit sollte diese Bijektion ein Homöomorphismus sein, sonst ist das Ergebnis keine topologische Mannigfaltigkeit. Ebenso muss es sich bei einer differenzierbaren Mannigfaltigkeit um einen Diffeomorphismus handeln. Für andere Verteiler sollten andere Strukturen erhalten bleiben.
Ein endlicher Zylinder kann als Mannigfaltigkeit konstruiert werden, indem mit einem Streifen [0,1] × [0,1] begonnen und ein Paar gegenüberliegender Kanten durch einen geeigneten Diffeomorphismus an die Grenze geklebt wird. Eine projektive Ebene kann erhalten werden, indem eine Kugel mit einem Loch darin entlang ihrer jeweiligen kreisförmigen Grenzen auf einen Möbius-Streifen geklebt wird.
Kartesische Produkte
Das kartesische Produkt von Mannigfaltigkeiten ist ebenfalls eine Mannigfaltigkeit.
Die Dimension der Produktmannigfaltigkeit ist die Summe der Dimensionen ihrer Faktoren. Seine Topologie ist die Produkttopologie , und ein kartesisches Produkt von Diagrammen ist ein Diagramm für die Produktmannigfaltigkeit. Somit kann ein Atlas für die Produktmannigfaltigkeit unter Verwendung von Atlanten für seine Faktoren konstruiert werden. Definieren diese Atlanten eine Differentialstruktur der Faktoren, so definiert der entsprechende Atlas eine Differentialstruktur der Produktmannigfaltigkeit. Das gleiche gilt für jede andere Struktur, die auf den Faktoren definiert ist. Wenn einer der Faktoren einen Rand hat, hat auch die Produktmannigfaltigkeit einen Rand. Kartesische Produkte können verwendet werden, um Tori- und endliche Zylinder zu konstruieren , beispielsweise als S 1 × S 1 bzw. S 1 × [0,1].
Geschichte
Das Studium der Mannigfaltigkeiten vereint viele wichtige Bereiche der Mathematik: Es verallgemeinert Konzepte wie Kurven und Flächen sowie Ideen aus der linearen Algebra und der Topologie.
Frühe Entwicklung
Vor dem modernen Konzept einer Mannigfaltigkeit gab es mehrere wichtige Ergebnisse.
Nicht-euklidische Geometrie betrachtet Räume , in denen Euklid ‚s parallel Postulat ausfällt. Saccheri untersuchte erstmals 1733 solche Geometrien, versuchte aber nur, sie zu widerlegen. Gauss , Bolyai und Lobatschewski haben sie 100 Jahre später unabhängig voneinander entdeckt. Ihre Forschung deckte zwei Arten von Räumen auf, deren geometrische Strukturen sich von denen des klassischen euklidischen Raums unterscheiden; diese führten zu hyperbolischer Geometrie und elliptischer Geometrie . In der modernen Mannigfaltigkeitstheorie entsprechen diese Begriffe den Riemannschen Mannigfaltigkeiten mit konstanter negativer bzw. positiver Krümmung .
Carl Friedrich Gauß war vielleicht der erste, der abstrakte Räume als eigenständige mathematische Objekte betrachtete. Sein Theorema egregium gibt eine Methode zur Berechnung der Krümmung einer Oberfläche ohne Berücksichtigung des Umgebungsraums, in dem die Oberfläche liegt. Eine solche Oberfläche würde in der modernen Terminologie eine Mannigfaltigkeit genannt; und in modernen Begriffen bewies der Satz, dass die Krümmung der Oberfläche eine intrinsische Eigenschaft ist . Die Mannigfaltigkeitstheorie konzentriert sich ausschließlich auf diese intrinsischen Eigenschaften (oder Invarianten), während die extrinsischen Eigenschaften des umgebenden Raums weitgehend ignoriert werden.
Ein weiteres, topologischeres Beispiel für eine intrinsische Eigenschaft einer Mannigfaltigkeit ist ihre Euler-Charakteristik . Leonhard Euler zeigte, dass für ein konvexes Polytop im dreidimensionalen euklidischen Raum mit V Ecken (oder Ecken), E Kanten und F Flächen
Synthese
Untersuchungen von Niels Henrik Abel und Carl Gustav Jacobi auf Umkehrung der elliptischen Integrale in der ersten Hälfte des 19. Jahrhunderts führte sie spezielle Arten komplexer Mannigfaltigkeiten zu betrachten, jetzt bekannt als Jacobi . Bernhard Riemann trug weiter zu ihrer Theorie bei, indem er die geometrische Bedeutung des Prozesses der analytischen Fortsetzung von Funktionen komplexer Variablen klärte .
Eine weitere wichtige Quelle für Mannigfaltigkeiten in der Mathematik des 19. Jahrhunderts war die analytische Mechanik , wie sie von Siméon Poisson , Jacobi und William Rowan Hamilton entwickelt wurde . Die möglichen Zustände eines mechanischen Systems werden als Punkte eines abstrakten Raums angesehen, des Phasenraums in den Lagrangeschen und Hamiltonschen Formalismen der klassischen Mechanik. Dieser Raum ist in der Tat eine hochdimensionale Mannigfaltigkeit, deren Dimension den Freiheitsgraden des Systems entspricht und in der die Punkte durch ihre verallgemeinerten Koordinaten angegeben sind . Für eine uneingeschränkte Bewegung freier Teilchen ist die Mannigfaltigkeit äquivalent zum euklidischen Raum, aber verschiedene Erhaltungssätze beschränken sie auf kompliziertere Formationen, zB Liouville tori . Die im 18. Jahrhundert von Leonhard Euler und Joseph-Louis Lagrange entwickelte Theorie eines rotierenden Festkörpers liefert ein weiteres Beispiel, bei dem die Mannigfaltigkeit nicht trivial ist. Geometrische und topologische Aspekte der klassischen Mechanik wurden von Henri Poincaré , einem der Begründer der Topologie, hervorgehoben.
Riemann war der erste, der umfangreiche Arbeiten zur Verallgemeinerung der Idee einer Oberfläche auf höhere Dimensionen durchgeführt hat. Der Name Mannigfaltigkeit stammt von Riemanns ursprünglichem deutschen Begriff Mannigfaltigkeit , den William Kingdon Clifford mit "Mannigfaltigkeit" übersetzt hat. In seiner Göttinger Antrittsvorlesung beschrieb Riemann die Menge aller möglichen Werte einer Variablen mit gewissen Randbedingungen als Mannigfaltigkeit , da die Variable viele Werte haben kann. Er unterscheidet zwischen stetiger Mannigfaltigkeit und diskreter Mannigfaltigkeit ( stetige Mannigfaltigkeit und unstetige Mannigfaltigkeit ), je nachdem, ob sich der Wert stetig ändert oder nicht. Als kontinuierliche Beispiele nennt Riemann nicht nur Farben und die Lage von Objekten im Raum, sondern auch die möglichen Formen einer Raumfigur. Mittels Induktion konstruiert Riemann eine n-fach ausgedehnte Mannigfaltigkeit ( n-mal ausgedehnte Mannigfaltigkeit oder n-dimensionale Mannigfaltigkeit ) als stetigen Stapel von (n−1) dimensionalen Mannigfaltigkeiten. Riemanns intuitiver Begriff einer Mannigfaltigkeit entwickelte sich zu dem, was heute als Mannigfaltigkeit formalisiert wird. Riemannsche Mannigfaltigkeiten und Riemannsche Flächen sind nach Riemann benannt.
Poincarés Definition
In seiner sehr einflussreichen Arbeit Analysis Situs gab Henri Poincaré eine Definition einer differenzierbaren Mannigfaltigkeit ( variété ), die als Vorläufer des modernen Konzepts einer Mannigfaltigkeit diente.
Im ersten Abschnitt von Analysis Situs definiert Poincaré eine Mannigfaltigkeit als die Niveaumenge einer stetig differenzierbaren Funktion zwischen euklidischen Räumen, die die Nichtentartungshypothese des impliziten Funktionssatzes erfüllt . Im dritten Abschnitt bemerkt er zunächst, dass der Graph einer stetig differenzierbaren Funktion eine Mannigfaltigkeit im letzteren Sinne ist. Er schlägt dann eine neue, allgemeinere Definition der Mannigfaltigkeit vor, die auf einer 'Kette von Mannigfaltigkeiten' ( une chaîne des variétés ) basiert .
Poincarés Begriff einer Kette von Mannigfaltigkeiten ist ein Vorläufer des modernen Atlasbegriffs. Insbesondere betrachtet er zwei Mannigfaltigkeiten, die jeweils als Funktionsgraphen und definiert sind . Überlappen sich diese Mannigfaltigkeiten (
a une partie commune ), so verlangt er, dass die Koordinaten stetig differenzierbar von den Koordinaten abhängen und umgekehrt (' ...les sont fonctions analytiques des et inversement '). Auf diese Weise führt er einen Vorläufer des Begriffs Chart und Transition Map ein .Beispielsweise kann man sich den Einheitskreis in der Ebene als Graph der Funktion vorstellen oder auch als Funktion in der Umgebung jedes Punktes außer den Punkten (1, 0) und (-1, 0); und in einer Umgebung dieser Punkte kann man es sich als den Graphen von bzw. und vorstellen . Der Kreis kann durch einen Graphen in der Nähe jedes Punktes dargestellt werden, da die linke Seite seiner Definitionsgleichung an jedem Punkt des Kreises einen Gradienten ungleich Null hat. Nach dem
impliziten Funktionssatz ist jede Untermannigfaltigkeit des euklidischen Raums lokal der Graph einer Funktion.Hermann Weyl gab in seiner Vorlesung über Riemannsche Flächen 1911–1912 eine intrinsische Definition für differenzierbare Mannigfaltigkeiten und ebnete damit den Weg zum allgemeinen Konzept eines topologischen Raums , der kurz darauf folgte. In den 1930er Jahren klärten Hassler Whitney und andere die grundlegenden Aspekte des Themas, und so wurden Intuitionen aus der zweiten Hälfte des 19. Jahrhunderts präzise und durch Differentialgeometrie und Lie-Gruppentheorie entwickelt. Bemerkenswerterweise zeigte das Whitney-Einbettungstheorem , dass die intrinsische Definition in Bezug auf Karten der Poincaré-Definition in Bezug auf Teilmengen des euklidischen Raums äquivalent war.
Topologie von Mannigfaltigkeiten: Highlights
Zweidimensionale Mannigfaltigkeiten, auch bekannt als 2D- Flächen, eingebettet in unseren gemeinsamen 3D-Raum, wurden von Riemann unter dem Deckmantel der Riemann-Flächen betrachtet und Anfang des 20. Jahrhunderts von Poul Heegaard und Max Dehn streng klassifiziert . Poincaré leistete Pionierarbeit in der Erforschung dreidimensionaler Mannigfaltigkeiten und stellte eine grundlegende Frage zu ihnen, die heute als Poincaré-Vermutung bekannt ist . Nach fast einem Jahrhundert bewies Grigori Perelman die Poincaré-Vermutung (siehe Lösung der Poincaré-Vermutung ). William Thurston ‚s Geometrisierung Programm , in den 1970er Jahren formuliert, vorausgesetzt , eine weitreichende Verlängerung der Poincaré - Vermutung zu den allgemeinen dreidimensionalen Mannigfaltigkeiten. Vierdimensionale Mannigfaltigkeiten wurden in den 1980er Jahren von Michael Freedman in den Vordergrund der mathematischen Forschung gestellt und in einem anderen Kontext von Simon Donaldson , der durch die damals jüngsten Fortschritte in der theoretischen Physik ( Yang-Mills-Theorie ) motiviert war , wo sie als ein Ersatz für die gewöhnliche 'flache' Raumzeit . Andrey Markov Jr. zeigte 1960, dass es keinen Algorithmus zur Klassifizierung von vierdimensionalen Mannigfaltigkeiten gibt. Wichtige Arbeiten zu höherdimensionalen Mannigfaltigkeiten, einschließlich Analoga der Poincaré-Vermutung , wurden früher von René Thom , John Milnor , Stephen Smale und Sergei Novikov durchgeführt . Eine sehr durchdringende und flexible Technik, die vielen Arbeiten zur Topologie von Mannigfaltigkeiten zugrunde liegt, ist die Morsetheorie .
Zusätzliche Struktur
Topologische Mannigfaltigkeiten
Die am einfachsten zu definierende Mannigfaltigkeit ist die topologische Mannigfaltigkeit, die lokal wie ein "gewöhnlicher" euklidischer Raum aussieht . Per Definition sind alle Mannigfaltigkeiten topologische Mannigfaltigkeiten, daher wird der Ausdruck "topologische Mannigfaltigkeit" normalerweise verwendet, um hervorzuheben, dass einer Mannigfaltigkeit zusätzliche Struktur fehlt oder dass nur ihre topologischen Eigenschaften berücksichtigt werden. Formal ist eine topologische Mannigfaltigkeit ein topologischer Raum, der
lokal homöomorph zu einem euklidischen Raum ist. Dies bedeutet, dass jeder Punkt eine Umgebung hat, für die es einen Homöomorphismus gibt (eine bijektiv stetige Funktion, deren Inverse ebenfalls stetig ist), die diese Umgebung auf abbildet . Diese Homöomorphismen sind die Diagramme der Mannigfaltigkeit.Eine topologische Mannigfaltigkeit sieht lokal eher schwach aus wie ein euklidischer Raum: Während es für jede einzelne Karte möglich ist, differenzierbare Funktionen zu unterscheiden oder Entfernungen und Winkel zu messen, hat ein Raum allein dadurch, dass er eine topologische Mannigfaltigkeit ist, keine besondere und konsistente Auswahl solcher Konzepte. Um solche Eigenschaften für eine Mannigfaltigkeit zu diskutieren, muss man weitere Strukturen spezifizieren und differenzierbare Mannigfaltigkeiten und Riemannsche Mannigfaltigkeiten betrachten, die unten diskutiert werden. Insbesondere kann dieselbe zugrundeliegende topologische Mannigfaltigkeit mehrere miteinander inkompatible Klassen von differenzierbaren Funktionen und eine unendliche Anzahl von Möglichkeiten haben, Abstände und Winkel zu spezifizieren.
Üblicherweise werden zusätzliche technische Annahmen über den topologischen Raum gemacht, um pathologische Fälle auszuschließen. Es ist üblich zu verlangen, dass der Raum Hausdorff und der zweite abzählbar ist .
Die Dimension der Mannigfaltigkeit an einem bestimmten Punkt ist die Dimension des euklidischen Raums, auf den die Karten an diesem Punkt abgebildet werden (Nummer n in der Definition). Alle Punkte einer zusammenhängenden Mannigfaltigkeit haben die gleiche Dimension. Einige Autoren verlangen, dass alle Karten einer topologischen Mannigfaltigkeit auf euklidische Räume derselben Dimension abbilden. In diesem Fall hat jede topologische Mannigfaltigkeit eine topologische Invariante, ihre Dimension.
Differenzierbare Mannigfaltigkeiten
Für die meisten Anwendungen wird eine spezielle topologische Mannigfaltigkeit verwendet, nämlich eine differenzierbare Mannigfaltigkeit . Wenn die lokalen Karten auf einer Mannigfaltigkeit in gewissem Sinne kompatibel sind, kann man Richtungen, Tangentialräume und differenzierbare Funktionen auf dieser Mannigfaltigkeit definieren. Insbesondere ist es möglich, Kalkül auf einer differenzierbaren Mannigfaltigkeit anzuwenden . Jeder Punkt einer n- dimensionalen differenzierbaren Mannigfaltigkeit hat einen Tangentialraum . Dies ist ein n- dimensionaler euklidischer Raum, der aus den Tangentenvektoren der Kurven durch den Punkt besteht.
Zwei wichtige Klassen differenzierbarer Mannigfaltigkeiten sind glatte und analytische Mannigfaltigkeiten . Für glatte Mannigfaltigkeiten sind die Übergangsabbildungen glatt, dh unendlich differenzierbar. Analytische Mannigfaltigkeiten sind glatte Mannigfaltigkeiten mit der zusätzlichen Bedingung, dass die Übergangskarten analytisch sind (sie können als Potenzreihen ausgedrückt
werden ). Der Kugel kann eine analytische Struktur gegeben werden, ebenso wie die meisten bekannten Kurven und Flächen.Eine korrigierbare Menge verallgemeinert die Idee einer stückweise glatten oder korrigierbaren Kurve auf höhere Dimensionen; jedoch sind rektifizierbare Mengen im Allgemeinen keine Mannigfaltigkeiten.
Riemannsche Mannigfaltigkeiten
Um Abstände und Winkel auf Mannigfaltigkeiten zu messen, muss die Mannigfaltigkeit Riemannsch sein. Eine Riemannsche Mannigfaltigkeit ist eine differenzierbare Mannigfaltigkeit, bei der jeder Tangentialraum mit einem inneren Produkt ⟨⋅ , ⋅⟩ ausgestattet ist , das von Punkt zu Punkt glatt variiert. Bei zwei Tangentenvektoren u und v ergibt das innere Produkt ⟨ u , v ⟩ eine reelle Zahl. Das Punktprodukt (oder Skalarprodukt) ist ein typisches Beispiel für ein inneres Produkt. Dies ermöglicht es, verschiedene Begriffe wie Länge, Winkel , Flächen (oder Volumen ), Krümmung und Divergenz von Vektorfeldern zu definieren .
Allen differenzierbaren Mannigfaltigkeiten (von konstanter Dimension) kann die Struktur einer Riemannschen Mannigfaltigkeit gegeben werden. Der euklidische Raum selbst trägt eine natürliche Struktur der Riemannschen Mannigfaltigkeit (die Tangentialräume werden natürlich mit dem euklidischen Raum selbst identifiziert und tragen das Standardskalarprodukt des Raums). Viele bekannte Kurven und Flächen, darunter zum Beispiel alle n- Kugeln, werden als Unterräume eines euklidischen Raums angegeben und erben eine Metrik von ihrer Einbettung in diesen.
Finsler-Verteiler
Eine Finsler-Mannigfaltigkeit ermöglicht die Definition von Entfernungen, erfordert jedoch nicht das Konzept des Winkels; es ist eine analytische Mannigfaltigkeit, in der jeder Tangentialraum mit einer Norm , ||·||, ausgestattet
ist , die von Punkt zu Punkt glatt variiert. Diese Norm kann zu einer Metrik erweitert werden , die die Länge einer Kurve definiert; aber es kann im Allgemeinen nicht verwendet werden, um ein inneres Produkt zu definieren.Jede Riemannsche Mannigfaltigkeit ist eine Finslersche Mannigfaltigkeit.
Lügengruppen
Lie-Gruppen , benannt nach Sophus Lie , sind differenzierbare Mannigfaltigkeiten, die auch die Struktur einer Gruppe tragen , so dass die Gruppenoperationen durch glatte Abbildungen definiert werden.
Ein euklidischer Vektorraum mit der Gruppenoperation der Vektoraddition ist ein Beispiel für eine nicht kompakte Lie-Gruppe. Ein einfaches Beispiel für eine kompakte Lie-Gruppe ist der Kreis: Die Gruppenoperation ist einfach Rotation. Diese Gruppe, bekannt als U(1), kann auch als die Gruppe der komplexen Zahlen vom Modul 1 mit Multiplikation als Gruppenoperation charakterisiert werden.
Andere Beispiele für Lie-Gruppen umfassen spezielle Gruppen von Matrizen , die alle Untergruppen der allgemeinen linearen Gruppe sind , der Gruppe von n mal n Matrizen mit einer Determinante ungleich null. Wenn die Matrixeinträge reelle Zahlen sind , handelt es sich um eine n 2 -dimensionale unzusammenhängende Mannigfaltigkeit. Die orthogonalen Gruppen , die Symmetriegruppen der Kugel und Hypersphären , sind n ( n −1)/2 dimensionale Mannigfaltigkeiten, wobei n −1 die Dimension der Kugel ist. Weitere Beispiele finden Sie in der Tabelle der Lie-Gruppen .
Andere Arten von Verteilern
- Eine komplexe Mannigfaltigkeit ist eine Mannigfaltigkeit, deren Diagramme Werte aufnehmen und deren Übergangsfunktionen auf den Überlappungen
Klassifikation und Invarianten
Unterschiedliche Vorstellungen von Mannigfaltigkeiten haben unterschiedliche Vorstellungen von Klassifikation und Invariante; In diesem Abschnitt konzentrieren wir uns auf glatte geschlossene Mannigfaltigkeiten.
Die Klassifikation glatter geschlossener Mannigfaltigkeiten ist im Prinzip gut verstanden , außer in Dimension 4 : in niedrigen Dimensionen (2 und 3) ist sie geometrisch, über den Uniformisierungssatz und die Lösung der Poincaré-Vermutung , und in hoher Dimension (5 und höher) es ist algebraisch, über die Chirurgietheorie . Dies ist eine prinzipielle Klassifikation: Die allgemeine Frage, ob zwei glatte Mannigfaltigkeiten diffeomorph sind, ist im Allgemeinen nicht berechenbar. Darüber hinaus bleiben spezifische Berechnungen schwierig, und es gibt viele offene Fragen.
Orientierbare Oberflächen können nach Gattung visualisiert und ihre Diffeomorphismusklassen aufgezählt werden. Bei zwei orientierbaren Oberflächen kann man feststellen, ob sie diffeomorph sind, indem man ihre jeweiligen Gattungen berechnet und vergleicht: Sie sind genau dann diffeomorph, wenn die Gattungen gleich sind, also bildet die Gattung einen vollständigen Satz von Invarianten .
Dies ist in höheren Dimensionen viel schwieriger: Höherdimensionale Mannigfaltigkeiten können nicht direkt visualisiert werden (obwohl visuelle Intuition nützlich ist, um sie zu verstehen), noch können ihre Diffeomorphismusklassen aufgezählt werden, noch kann man allgemein feststellen, ob zwei verschiedene Beschreibungen einer höherdimensionalen Mannigfaltigkeit beziehen sich auf das gleiche Objekt.
Man kann jedoch feststellen, ob zwei Mannigfaltigkeiten unterschiedlich sind, wenn es eine intrinsische Eigenschaft gibt, die sie unterscheidet. Solche Kriterien werden als allgemein bezeichnet Invarianten , weil, während sie in Bezug auf irgendeine Darstellung (wie die Gattung im Sinne einer Triangulation) definiert werden können, sie gleich in Bezug auf alle möglichen Beschreibungen eines bestimmten vielfältig sind: sie sind invariant unter verschiedenen Beschreibungen.
Naiv könnte man hoffen, ein Arsenal invarianten Kriterien zu entwickeln, das alle Mannigfaltigkeiten bis auf Isomorphie endgültig klassifizieren würde. Leider ist bekannt, dass für Mannigfaltigkeiten der Dimension 4 und höher kein Programm existiert , das entscheiden kann, ob zwei Mannigfaltigkeiten diffeomorph sind.
Glatte Mannigfaltigkeiten haben eine Vielzahl von Invarianten , die aus der Punktmengentopologie , der klassischen algebraischen Topologie und der geometrischen Topologie stammen . Die bekanntesten Invarianten, die für Oberflächen sichtbar sind, sind die Orientierbarkeit (eine normale Invariante, die auch durch Homologie nachgewiesen wird ) und die Gattung (eine homologische Invariante).
Glatte geschlossene Mannigfaltigkeiten haben keine lokalen Invarianten (außer Dimension), obwohl geometrische Mannigfaltigkeiten lokale Invarianten haben, insbesondere die Krümmung einer Riemannschen Mannigfaltigkeit und die Torsion einer Mannigfaltigkeit, die mit einer affinen Verbindung ausgestattet ist . Diese Unterscheidung zwischen lokalen Invarianten und keinen lokalen Invarianten ist eine übliche Methode, um zwischen Geometrie und Topologie zu unterscheiden . Alle Invarianten einer glatten geschlossenen Mannigfaltigkeit sind also global.
Die algebraische Topologie ist eine Quelle für eine Reihe wichtiger globaler invarianten Eigenschaften. Zu den Schlüsselkriterien zählen die einfach zusammenhängende Eigenschaft und Orientierbarkeit (siehe unten). Tatsächlich wurden mehrere Zweige der Mathematik wie die Homologie- und Homotopietheorie und die Theorie der charakteristischen Klassen gegründet, um invariante Eigenschaften von Mannigfaltigkeiten zu studieren.
Oberflächen
Orientierungsfähigkeit
In Dimensionen zwei und höher ist ein einfaches, aber wichtiges invariantes Kriterium die Frage, ob eine Mannigfaltigkeit eine sinnvolle Orientierung zulässt. Betrachten Sie eine topologische Mannigfaltigkeit mit Diagrammen, die auf . Bei einer
geordneten Basis für bewirkt ein Diagramm, dass sein Teil der Mannigfaltigkeit selbst ein Ordnungsgefühl bekommt, das in 3-Dimensionen entweder als rechtshändig oder linkshändig angesehen werden kann. Überlappende Diagramme müssen in ihrem Ordnungssinn nicht übereinstimmen, was den Mannigfaltigkeiten eine wichtige Freiheit gibt. Für einige Mannigfaltigkeiten, wie die Kugel, können Diagramme so gewählt werden, dass überlappende Regionen in ihrer "Händigkeit" übereinstimmen; das sind orientierbare Mannigfaltigkeiten. Für andere ist dies unmöglich. Die letztere Möglichkeit ist leicht zu übersehen, da jede geschlossene Fläche, die (ohne Selbstüberschneidung) in den dreidimensionalen Raum eingebettet ist, orientierbar ist.Einige anschauliche Beispiele für nicht orientierbare Mannigfaltigkeiten sind: (1) der Möbiusstreifen , der eine Mannigfaltigkeit mit Rand ist, (2) die Kleinsche Flasche , die sich in ihrer 3-Raum-Darstellung schneiden muss, und (3) die reelle projektive Ebene , die natürlich in der Geometrie entsteht.
Möbiusband
Beginnen Sie mit einem senkrecht stehenden unendlichen Kreiszylinder, einer Mannigfaltigkeit ohne Begrenzung. Schneiden Sie hoch und tief darüber, um zwei kreisförmige Grenzen und den zylindrischen Streifen dazwischen zu erzeugen. Dies ist eine orientierbare Mannigfaltigkeit mit Grenze, an der "chirurgisch" durchgeführt wird. Schneiden Sie den Streifen auf, damit er sich zu einem Rechteck aufrollen kann, aber halten Sie die abgeschnittenen Enden fest. Drehen Sie ein Ende um 180°, so dass die Innenfläche nach außen zeigt, und kleben Sie die Enden wieder nahtlos zusammen. So entsteht ein Streifen mit permanenter Halbdrehung: der Möbius-Streifen. Seine Grenze ist nicht mehr ein Kreispaar, sondern (topologisch) ein einzelner Kreis; und was einst sein "innen" war, ist mit seinem "außen" verschmolzen, so dass es nur noch eine einzige Seite hat. Ähnlich wie bei der Kleinen Flasche unten müsste sich diese zweidimensionale Oberfläche in zwei Dimensionen schneiden, kann aber leicht in drei oder mehr Dimensionen konstruiert werden.
Kleinflasche

Nehmen Sie zwei Möbius-Streifen; jeder hat eine einzelne Schleife als Grenze. Richten Sie diese Schleifen zu Kreisen aus und lassen Sie die Streifen zu Kreuzkappen verzerren . Durch das Zusammenkleben der Kreise entsteht eine neue, geschlossene Mannigfaltigkeit ohne Begrenzung, die Klein-Flasche. Das Schließen der Fläche trägt nicht zur Verbesserung der fehlenden Orientierungsfähigkeit bei, sondern entfernt lediglich die Grenze. Somit ist die Klein-Flasche eine geschlossene Fläche ohne Unterscheidung zwischen Innen und Außen. Im dreidimensionalen Raum muss die Oberfläche einer Klein-Flasche durch sich selbst hindurchgehen. Der Bau einer Klein-Flasche, die sich nicht selbst schneidet, erfordert vier oder mehr Raumdimensionen.
Echte projektive Ebene
Beginnen Sie mit einer Kugel, die auf den Ursprung zentriert ist. Jede Linie durch den Ursprung durchdringt die Kugel an zwei gegenüberliegenden Punkten, die als Antipoden bezeichnet werden . Obwohl dies physikalisch nicht möglich ist, ist es (durch Betrachtung eines Quotientenraums ) möglich, jedes Antipodenpaar mathematisch zu einem einzigen Punkt zu verschmelzen. Die so erzeugte geschlossene Fläche ist die reale projektive Ebene, noch eine weitere nicht orientierbare Fläche. Es hat eine Reihe von gleichwertigen Beschreibungen und Konstruktionen, aber diese Route erklärt ihren Namen: Alle Punkte auf einer bestimmten Linie durch den Ursprung projizieren auf denselben "Punkt" auf dieser "Ebene".
Gattung und das Euler-Merkmal
Für zweidimensionale Mannigfaltigkeiten ist eine wichtige invariante Eigenschaft die Gattung oder die "Anzahl der Griffe", die in einer Oberfläche vorhanden sind. Ein Torus ist eine Kugel mit einem Griff, ein Doppeltorus ist eine Kugel mit zwei Griffen und so weiter. Tatsächlich ist es möglich, kompakte, zweidimensionale Mannigfaltigkeiten auf der Grundlage von Gattung und Orientierbarkeit vollständig zu charakterisieren. In höherdimensionalen Mannigfaltigkeiten wird die Gattung durch den Begriff der Euler-Charakteristik und allgemeiner Betti-Zahlen und Homologie und Kohomologie ersetzt .
Karten von Verteilern
So wie es verschiedene Arten von Mannigfaltigkeiten gibt, gibt es verschiedene Arten von Karten von Mannigfaltigkeiten . Neben stetigen Funktionen und glatten Funktionen im Allgemeinen gibt es Abbildungen mit besonderen Eigenschaften. Ein grundlegender Typ in der geometrischen Topologie sind Einbettungen , für die die Knotentheorie ein zentrales Beispiel ist, und Verallgemeinerungen wie Immersionen , Eintauchen , Überdeckungsräume und verzweigte Überdeckungsräume . Zu den grundlegenden Ergebnissen gehören das Whitney-Einbettungstheorem und das Whitney-Immersionstheorem .
In der Riemannschen Geometrie kann man nach Karten fragen, um die Riemannsche Metrik zu bewahren, was zu Begriffen von isometrischen Einbettungen , isometrischen Immersionen und Riemannschen Eintauchungen führt ; ein grundlegendes Ergebnis ist das Einbettungstheorem von Nash .
Skalarwertige Funktionen
Ein grundlegendes Beispiel für Abbildungen zwischen Mannigfaltigkeiten sind skalarwertige Funktionen auf einer Mannigfaltigkeit,
manchmal als reguläre Funktionen oder Funktionale bezeichnet , in Analogie zur algebraischen Geometrie oder linearen Algebra. Diese sind sowohl für sich als auch für das Studium der zugrunde liegenden Mannigfaltigkeit von Interesse.
In der geometrischen Topologie werden am häufigsten Morsefunktionen untersucht , die Handlebody- Zerlegungen liefern , während man in der mathematischen Analyse oft die Lösung partieller Differentialgleichungen untersucht , von denen ein wichtiges Beispiel die harmonische Analyse ist , bei der harmonische Funktionen untersucht werden : der Kern des Laplace Betreiber . Dies führt zu Funktionen wie den sphärischen Harmonischen und zu Heat-Kernel- Methoden zum Studium von Mannigfaltigkeiten, wie dem Hören der Form einer Trommel und einigen Beweisen des Atiyah-Singer-Indexsatzes .
Verallgemeinerungen von Mannigfaltigkeiten
- Unendlichdimensionale Mannigfaltigkeiten
- Die Definition einer Mannigfaltigkeit kann verallgemeinert werden, indem die Forderung nach endlicher Dimensionalität fallengelassen wird. Somit ist eine unendlichdimensionale Mannigfaltigkeit ein topologischer Raum, der lokal homöomorph zu einem topologischen Vektorraum über den reellen Zahlen ist. Dies lässt die Punktmengen-Axiome weg und erlaubt höhere Kardinalitäten und Nicht-Hausdorff-Mannigfaltigkeiten ; und es lässt endliche Dimension weg, wodurch Strukturen wie Hilbert-Mannigfaltigkeiten auf Hilbert-Räumen , Banach-Mannigfaltigkeiten auf Banach-Räumen und Fréchet-Mannigfaltigkeiten auf Fréchet-Räumen modelliert
Siehe auch
- Geodätisch – Kürzester Weg auf einer gekrümmten Fläche oder einer Riemannschen Mannigfaltigkeit
- Richtungsstatistik : Statistiken über Mannigfaltigkeiten
- Liste der Verteiler – Wikipedia-Listenartikel
- Zeitleiste der Mannigfaltigkeiten –
Nach Dimension
- 3-Mannigfaltigkeit – Raum, der lokal wie ein euklidischer dreidimensionaler Raum aussieht
- 4-Verteiler – Verteiler der Dimension vier
- 5-Verteiler – Verteiler der Dimension fünf
- Vielfältige Zuordnungen
Anmerkungen
Verweise
- Freedman, Michael H. und Quinn, Frank (1990) Topology of 4-Manifolds . Princeton University Press. ISBN 0-691-08577-3 .
- Guillemin, Victor und Pollack, Alan (1974) Differentielle Topologie . Lehrlingssaal. ISBN 0-13-212605-2 . Von Milnor inspirierter Text für Fortgeschrittene im Grundstudium / Erstsemester.
- Hempel, John (1976) 3-Manifolds . Princeton University Press. ISBN 0-8218-3695-1 .
- Hirsch, Morris , (1997) Differentielle Topologie . Springer-Verlag. ISBN 0-387-90148-5 . Der vollständigste Bericht mit historischen Einblicken und hervorragenden, aber schwierigen Problemen. Das Standard-Nachschlagewerk für alle, die ein tiefes Verständnis des Themas haben möchten.
- Kirby, Robion C. und Siebenmann, Laurence C. (1977) Foundational Essays on Topological Manifolds. Glättungen und Triangulationen . Princeton University Press. ISBN 0-691-08190-5 . Eine detaillierte Untersuchung der Kategorie der topologischen Mannigfaltigkeiten.
- Lee, John M. (2000) Einführung in topologische Mannigfaltigkeiten . Springer-Verlag. ISBN 0-387-98759-2 . Ausführlicher und umfassender Erstsemestertext.
- Lee, John M. (2003) Einführung in glatte Manifolds . Springer-Verlag. ISBN 0-387-95495-3 . Ausführlicher und umfassender Erstsemestertext; Fortsetzung von Einführung in topologische Mannigfaltigkeiten .
- Massey, William S. (1977) Algebraische Topologie: Eine Einführung . Springer-Verlag. ISBN 0-387-90271-6 .
- Milnor, John (1997) Topologie aus der differenzierbaren Sicht . Princeton University Press. ISBN 0-691-04833-9 . Klassische kurze Einführung in die Differentialtopologie.
- Munkres, James R. (1991) Analysis on Manifolds . Addison-Wesley (nachgedruckt von Westview Press) ISBN 0-201-51035-9 . Bachelor-Text zur Behandlung von Mannigfaltigkeiten in .
- Munkres, James R. (2000) Topologie . Lehrlingssaal. ISBN 0-13-181629-2 .
- Neuwirth, LP, Hrsg. (1975) Knoten, Gruppen und 3-Manifolds. Papiere, die dem Andenken an RH Fox gewidmet sind . Princeton University Press. ISBN 978-0-691-08170-0 .
-
Riemann, Bernhard , Gesammelte mathematische Werke und wissenschaftlicher Nachlass , Sändig Reprint. ISBN 3-253-03059-8 .
- Grundlagen für eine allgemeine Theorie der Funktionen einer veränderlichen komplexen Grösse. 1851 Doktorarbeitin der "manifold" ( Mannigfaltigkeit ) zuerst erscheint.
- Ueber die Hypothesen, welche der Geometrie zu Grunde liegen. Die 1854 Göttinger Antrittsvorlesung ( Habilitationsschrift ).
- Spivak, Michael (1965) Calculus on Manifolds: A Modern Approach to Classical Theorems of Advanced Calculus . WA Benjamin Inc. (nachgedruckt von Addison-Wesley und Westview Press). ISBN 0-8053-9021-9 . Bekanntermaßen knapper Text für fortgeschrittene Studenten /
Externe Links
- "Manifold" , Enzyklopädie der Mathematik , EMS Press , 2001 [1994]
- Dimensions-math.org (Ein Film, der Mannigfaltigkeiten bis zur vierten Dimension erklärt und visualisiert.)
- Das vielfältige Atlas- Projekt des Max-Planck-Instituts für Mathematik in Bonn











![{\displaystyle {\begin{ausgerichtet}T(a)&=\chi_{\mathrm {rechts}}\left(\chi_{\mathrm {oben}}^{-1}\left[a\right] \right)\\&=\chi_{\textrm{right}}\left(a,{\sqrt {1-a^{2}}}\right)\\&={\sqrt {1-a^ {2}}}\end{ausgerichtet}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40ce5573c9fdbffd539c2d9a9f80fdd33ca68ae3)


![{\displaystyle {\begin{ausgerichtet}x&={\frac {1-s^{2}}{1+s^{2}}}\\[5pt]y&={\frac {2s}{1+s ^{2}}}\end{ausgerichtet}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f08d1a41825c29ff1f55d16dae15784d549e8179)