Riemann Krümmungstensor - Riemann curvature tensor

Generelle Relativität
${\displaystyle G_{\mu\nu}+\Lambda g_{\mu\nu}={8\pi G\over c^{4}}T_{\mu\nu}}$
Einführung Geschichte Mathematische Formulierung Tests
Grundsätzliche Konzepte Äquivalenzprinzip Spezielle Relativität Weltlinie Pseudo-Riemannsche Mannigfaltigkeit
Phänomene Kepler-Problem Gravitationslinsen Gravitationswellen Frame-Ziehen Geodätischer Effekt Ereignishorizont Singularität Schwarzes Loch Freizeit Raumzeit-Diagramme Minkowski-Raumzeit Einstein–Rosen-Brücke
Gleichungen Formalismen Gleichungen Linearisierte Schwerkraft Einstein-Feldgleichungen Friedmann Geodäten Mathisson–Papapetrou–Dixon Hamilton–Jacobi–Einstein Formalismen ADM BSSN Post-Newton Fortgeschrittene Theorie Kaluza-Klein-Theorie Quantengravitation
Lösungen Schwarzschild ( Innenraum ) Reissner–Nordström Gödel Kerr Kerr-Newman Kasner Lemaître–Tolman Taub-NUT Milne Robertson-Walker pp-Welle van Stockum Staub Weyl−Lewis−Papapetrou
Wissenschaftler Einstein Lorentz Hilbert Poincaré Schwarzschild de Sitter Reissner Nordström Weyl Eddington Friedman Milne Zwicky Lemaître Gödel Wheeler Robertson Bardeen Gehhilfe Kerr Chandrasekhar Ehlers Penrose Hawking Raychaudhuri Taylor Hulse van Stockum Taub Neuer Mann Yau Dorn Andere
Physikportal  Kategorie
v T e

Auf dem mathematischen Gebiet der Differentialgeometrie ist der Riemann-Krümmungstensor oder Riemann-Christoffel-Tensor (nach Bernhard Riemann und Elwin Bruno Christoffel ) die gebräuchlichste Art, die Krümmung Riemannscher Mannigfaltigkeiten auszudrücken . Es ordnet jedem Punkt einer Riemannschen Mannigfaltigkeit einen Tensor zu (dh es ist ein Tensorfeld ). Es ist eine lokale Invariante der Riemannschen Metrik, die das Versagen der zweiten kovarianten Ableitung misst, zu kommutieren. Eine Riemannsche Mannigfaltigkeit ist genau dann krümmungsnull, wenn sie flach , dh lokal isometrisch zum euklidischen Raum ist . Der Krümmungstensor kann auch für jede pseudo-Riemannsche Mannigfaltigkeit definiert werden , oder sogar jede Mannigfaltigkeit, die mit einer affinen Verbindung ausgestattet ist .

Sie ist ein zentrales mathematisches Werkzeug der Allgemeinen Relativitätstheorie , der modernen Gravitationstheorie , und die Krümmung der Raumzeit lässt sich prinzipiell über die geodätische Abweichungsgleichung beobachten . Der Krümmungstensor repräsentiert die Gezeitenkraft, die ein starrer Körper erfährt, der sich entlang einer Geodäte bewegt, in einem durch die Jacobi-Gleichung genau gemachten Sinn .

Definition

Sei ( M , g) eine Riemannsche oder Pseudo-Riemannsche Mannigfaltigkeit und der Raum aller Vektorfelder auf M. Wir definieren den Riemannschen Krümmungstensor als eine Abbildung durch die folgende Formel, die im Sinne der Levi-Civita-Verbindung ist : ${\displaystyle {\mathfrak{X}}(M)}$${\displaystyle R\colon {\mathfrak {X}}(M)\times {\mathfrak {X}}(M)\times {\mathfrak {X}}(M)\rightarrow {\mathfrak {X}}( M)}$ ${\displaystyle\nabla}$

${\displaystyle R(X,Y)Z=\nabla _{X}\nabla _{Y}Z-\nabla _{Y}\nabla _{X}Z-\nabla _{[X,Y]}Z }$

oder gleichwertig

${\displaystyle R(X,Y)=[\nabla_{X},\nabla_{Y}]-\nabla_{[X,Y]}}$

wobei [ X , Y ] die Lie-Klammer von Vektorfeldern und ein Kommutator von Differentialoperatoren ist. Für jedes Paar von Tangentenvektoren u , v ist R ( u , v ) eine lineare Transformation des Tangentialraums der Mannigfaltigkeit. Sie ist in u und v linear und definiert somit einen Tensor. Gelegentlich wird der Krümmungstensor mit umgekehrtem Vorzeichen definiert. ${\displaystyle [\nabla_{X},\nabla_{Y}]}$

Wenn und Koordinatenvektorfelder sind, dann vereinfacht sich die Formel zu ${\displaystyle X=\partial /\partial x^{i}}$${\displaystyle Y=\partial /\partial x^{j}}$${\displaystyle [X,Y]=0}$

${\displaystyle R(X,Y)Z=\nabla_{X}\nabla_{Y}Z-\nabla_{Y}\nabla_{X}Z.}$

Der Krümmungstensor misst die Nichtkommutativität der kovarianten Ableitung und ist als solcher das Integrabilitätshindernis für die Existenz einer Isometrie mit euklidischem Raum (in diesem Zusammenhang flacher Raum genannt). Die lineare Transformation wird auch Krümmungstransformation oder Endomorphismus genannt . ${\displaystyle w\mapsto R(u,v)w}$

Die Krümmungsformel kann auch durch die zweite kovariante Ableitung ausgedrückt werden, die definiert ist als:

${\displaystyle \nabla_{u,v}^{2}w=\nabla_{u}\nabla_{v}w-\nabla_{\nabla_{u}v}w}$

die in u und v linear ist . Dann:

${\displaystyle R(u,v)=\nabla_{u,v}^{2}-\nabla_{v,u}^{2}}$

Im allgemeinen Fall der Nichtkoordinatenvektoren u und v misst der Krümmungstensor also die Nichtkommutativität der zweiten kovarianten Ableitung.

Geometrische Bedeutung

Eine Darstellung der Motivation von Riemann Krümmung auf einer Kugel -ähnlichen vielfältig. Die Tatsache, dass dieser Transport am Startpunkt zwei verschiedene Vektoren definieren kann, führt zum Riemannschen Krümmungstensor. Das rechtwinklige Symbol bedeutet, dass das innere Produkt (durch den metrischen Tensor gegeben ) zwischen transportierten Vektoren (oder Tangentenvektoren der Kurven) 0 ist.

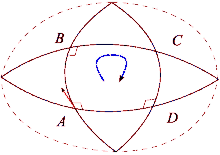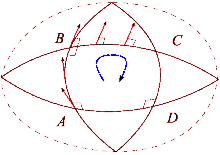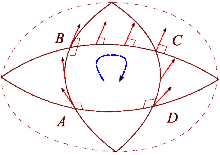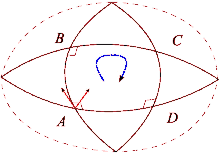
Informell

Man kann die Auswirkungen des gekrümmten Raums sehen, wenn man einen Tennisplatz und die Erde vergleicht. Beginnen Sie in der unteren rechten Ecke des Tennisplatzes mit einem Schläger in Richtung Norden. Stellen Sie dann, während Sie um den Umriss des Platzes gehen, bei jedem Schritt sicher, dass der Tennisschläger in der gleichen Ausrichtung parallel zu seinen vorherigen Positionen gehalten wird. Sobald die Schleife abgeschlossen ist, befindet sich der Tennisschläger parallel zu seiner ursprünglichen Ausgangsposition. Dies liegt daran, dass Tennisplätze so gebaut sind, dass die Oberfläche eben ist. Andererseits ist die Erdoberfläche gekrümmt: Wir können eine Schleife auf der Erdoberfläche machen. Beginnen Sie am Äquator und richten Sie einen Tennisschläger nach Norden entlang der Erdoberfläche. Auch hier sollte der Tennisschläger immer parallel zu seiner vorherigen Position bleiben, wobei die lokale Ebene des Horizonts als Referenz verwendet wird. Gehen Sie für diesen Weg zuerst zum Nordpol, drehen Sie sich dann um 90 Grad und gehen Sie hinunter zum Äquator, und drehen Sie sich schließlich um 90 Grad und gehen Sie zurück zum Ausgangspunkt. Jetzt zeigt der Tennisschläger jedoch nach hinten (nach Osten). Dieser Prozess ist vergleichbar mit dem parallelen Transportieren eines Vektors entlang des Pfads, und der Unterschied identifiziert, wie Linien, die "gerade" erscheinen, nur lokal "gerade" sind. Bei jedem Schleifendurchlauf wird der Tennisschläger abhängig von der Distanz und der Krümmung des Belags aus seiner Ausgangsposition weiter ausgelenkt. Es ist möglich, Pfade entlang einer gekrümmten Oberfläche zu identifizieren, auf denen der Paralleltransport wie auf ebenen Flächen funktioniert. Dies sind die Geodäten des Raums, zum Beispiel ein beliebiges Segment eines Großkreises einer Kugel.

Das Konzept eines gekrümmten Raums in der Mathematik unterscheidet sich vom Konversationsgebrauch. Wenn beispielsweise der obige Prozess an einem Zylinder durchgeführt wurde, würde man feststellen, dass er insgesamt nicht gekrümmt ist, da sich die Krümmung um den Zylinder mit der Ebenheit entlang des Zylinders aufhebt, dies ist eine Folge der Gaußschen Krümmung und des Gauß-Bonnet-Theorems . Ein bekanntes Beispiel dafür ist ein schlaffes Pizzastück, das entlang seiner Länge steif bleibt, wenn es entlang seiner Breite gebogen wird.

Der Riemann-Krümmungstensor ist eine Möglichkeit, ein Maß für die intrinsische Krümmung zu erfassen. Wenn Sie es in Bezug auf seine Komponenten aufschreiben (wie das Aufschreiben der Komponenten eines Vektors), besteht es aus einem mehrdimensionalen Array von Summen und Produkten partieller Ableitungen (manche dieser partiellen Ableitungen kann man sich als einfangen vorstellen die Krümmung, die jemandem auferlegt wird, der geradlinig auf einer gekrümmten Oberfläche geht).

Formal

Wenn ein Vektor in einem euklidischen Raum parallel um eine Schleife transportiert wird, zeigt er wieder in die ursprüngliche Richtung, nachdem er zu seiner ursprünglichen Position zurückgekehrt ist. Diese Eigenschaft gilt jedoch nicht im allgemeinen Fall. Der Riemannsche Krümmungstensor misst direkt das Versagen dieser in einer allgemeinen Riemannschen Mannigfaltigkeit . Dieses Versagen ist bekannt als nicht - Holonomie des Verteilers.

Sei x _t eine Kurve in einer Riemannschen Mannigfaltigkeit M . Bezeichne mit τ _{x t}  : T _{x 0} M → T _{x t} M die parallele Transportabbildung entlang x _t . Die parallelen Transportkarten beziehen sich auf die kovariante Ableitung durch

${\displaystyle \nabla _{{\dot {x}}_{0}}Y=\lim _{h\to 0}{\frac {1}{h}}\left(Y_{x_{0}} -\tau_{x_{h}}^{-1}\left(Y_{x_{h}}\right)\right)=\left.{\frac {d}{dt}}\left(\tau _{x_{t}}Y\right)\right|_{t=0}}$

für jedes entlang der Kurve definierte Vektorfeld Y.

Angenommen, X und Y sind ein Paar kommutierender Vektorfelder. Jedes dieser Felder erzeugt eine einparametrige Gruppe von Diffeomorphismen in einer Umgebung von x ₀ . Bezeichne mit τ _tX bzw. τ _tY die parallelen Transporte entlang der Flüsse von X und Y für die Zeit t . Paralleltransport eines Vektors Z ∈ T _{x 0} M um das Viereck mit den Seiten tY , sX , − tY , − sX ist gegeben durch

${\displaystyle \tau_{sX}^{-1}\tau_{tY}^{-1}\tau_{sX}\tau_{tY}Z.}$

Dies misst das Versagen des Paralleltransports, Z in seine ursprüngliche Position im Tangentialraum T _{x 0} M zurückzubringen . Das Verkleinern der Schleife durch Senden von s , t → 0 ergibt die infinitesimale Beschreibung dieser Abweichung:

${\displaystyle \left.{\frac {d}{ds}}{\frac {d}{dt}}\tau_{sX}^{-1}\tau_{tY}^{-1}\tau _{sX}\tau _{tY}Z\right|_{s=t=0}=\left(\nabla _{X}\nabla _{Y}-\nabla _{Y}\nabla _{X }-\nabla _{[X,Y]}\right)Z=R(X,Y)Z}$

wobei R der Riemannsche Krümmungstensor ist.

Koordinatenausdruck

Konvertiert in die Tensorindex-Notation ist der Riemannsche Krümmungstensor gegeben durch

${\displaystyle R^{\rho }{}_{\sigma\mu\nu}=dx^{\rho}\left(R\left(\partial_{\mu},\partial_{\nu}\ rechts)\partial _{\sigma}\rechts)}$

wo sind die Koordinatenvektorfelder. Der obige Ausdruck kann mit Christoffel-Symbolen geschrieben werden : ${\displaystyle \partial_{\mu}=\partial /\partial x^{\mu}}$

${\displaystyle R^{\rho }{}_{\sigma\mu\nu}=\partial_{\mu}\Gamma^{\rho }{}_{\nu\sigma}-\partial_{\ nu}\Gamma ^{\rho }{}_{\mu\sigma}+\Gamma^{\rho }{}_{\mu\lambda}\Gamma^{\lambda }{}_{\nu\sigma }-\Gamma^{\rho}{}_{\nu\lambda}\Gamma^{\lambda }{}_{\mu\sigma}}$

(Siehe auch die Liste der Formeln in der Riemannschen Geometrie ).

Der Riemannsche Krümmungstensor ist auch der Kommutator der kovarianten Ableitung eines beliebigen Kovektors mit sich selbst: ${\displaystyle A_{\nu}}$

${\displaystyle A_{\nu;\rho\sigma}-A_{\nu;\sigma\rho}=A_{\beta}R^{\beta }{}_{\nu\rho\sigma},}$

da die Verbindung torsionsfrei ist, was bedeutet, dass der Torsionstensor verschwindet. ${\displaystyle \Gamma^{\alpha}{}_{\beta\mu}}$ ${\displaystyle \Gamma^{\lambda }{}_{\mu\nu}-\Gamma^{\lambda }{}_{\nu\mu}}$

Diese Formel wird oft als Ricci-Identität bezeichnet . Dies ist die klassische Methode, die von Ricci und Levi-Civita verwendet wird , um einen Ausdruck für den Riemannschen Krümmungstensor zu erhalten. Damit ist der Tensorcharakter der Mengenmenge bewiesen. ${\displaystyle R^{\beta }{}_{\nu\rho\sigma}}$

Diese Identität kann verallgemeinert werden, um die Kommutatoren für zwei kovariante Ableitungen beliebiger Tensoren wie folgt zu erhalten

${\displaystyle {\begin{ausgerichtet}&\nabla_{\delta}\nabla_{\gamma}T^{\alpha_{1}\cdots\alpha_{r}}{}_{\beta_{ 1}\cdots\beta_{s}}-\nabla_{\gamma}\nabla_{\delta}T^{\alpha_{1}\cdots\alpha_{r}}{}_{\beta _{1}\cdots\beta_{s}}\\[3pt]={}&R^{\alpha_{1}}{}_{\rho\delta\gamma}T^{\rho\alpha_ {2}\cdots\alpha_{r}}{}_{\beta_{1}\cdots\beta_{s}}+\ldots+R^{\alpha_{r}}{}_{\ rho\delta\gamma}T^{\alpha_{1}\cdots\alpha_{r-1}\rho}{}_{\beta_{1}\cdots\beta_{s}}-R^ {\sigma }{}_{\beta_{1}\delta\gamma}T^{\alpha_{1}\cdots\alpha_{r}}{}_{\sigma\beta_{2}\ cdots \beta_{s}}-\ldots -R^{\sigma }{}_{\beta_{s}\delta\gamma}T^{\alpha_{1}\cdots \alpha_{r} }{}_{\beta_{1}\cdots\beta_{s-1}\sigma}\end{ausgerichtet}}}$

Diese Formel gilt unverändert auch für Tensordichten , denn für die Levi-Civita ( nicht generische ) Verbindung erhält man:

${\displaystyle \nabla_{\mu}\left({\sqrt {g}}\right)\equiv \left({\sqrt {g}}\right)_{;\mu}=0,}$

wo

${\displaystyle g=\left|\det\left(g_{\mu\nu}\right)\right|.}$

Manchmal ist es praktisch, auch die rein kovariante Version zu definieren durch

${\displaystyle R_{\rho\sigma\mu\nu}=g_{\rho\zeta}R^{\zeta }{}_{\sigma\mu\nu}.}$

Symmetrien und Identitäten

Der Riemannsche Krümmungstensor hat die folgenden Symmetrien und Identitäten:

Symmetrie verzerren	${\displaystyle R(u,v)=-R(v,u)}$	${\displaystyle R_{abcd}=-R_{abdc}\Leftrightarrow R_{ab(cd)}=0}$
Symmetrie verzerren	${\displaystyle \langle R(u,v)w,z\rangle =-\langle R(u,v)z,w\rangle}$	${\displaystyle R_{abcd}=-R_{bacd}\Leftrightarrow R_{(ab)cd}=0}$
Erste (algebraische) Bianchi-Identität	${\displaystyle R(u,v)w+R(v,w)u+R(w,u)v=0}$	${\displaystyle R_{abcd}+R_{acdb}+R_{adbc}=R_{a[bcd]}=0}$
Austauschsymmetrie	${\displaystyle \langle R(u,v)w,z\rangle =\langle R(w,z)u,v\rangle}$	${\displaystyle R_{abcd}=R_{cdab}}$
Zweite (differentielle) Bianchi-Identität	${\displaystyle \left(\nabla_{u}R\right)(v,w)+\left(\nabla_{v}R\right)(w,u)+\left(\nabla_{w} R\rechts)(u,v)=0}$	${\displaystyle R_{abcd;e}+R_{abde;c}+R_{abec;d}=R_{ab[cd;e]}=0}$

wobei sich die Klammer auf das innere Produkt auf dem Tangentialraum bezieht, das durch den metrischen Tensor induziert wird . ${\displaystyle\langle,\rangle}$

Die erste (algebraische) Bianchi-Identität wurde von Ricci entdeckt , wird aber oft als erste Bianchi-Identität oder algebraische Bianchi-Identität bezeichnet , weil sie der untenstehenden Bianchi- Identität ähnlich sieht . (Außerdem wird bei einer Torsion ungleich Null die erste Bianchi-Identität eine differentielle Identität des Torsionstensors .) . Es wird oft geschrieben:

$${\displaystyle R_{a[bcd]}=0,}$$

Die ersten drei Identitäten bilden eine vollständige Liste der Symmetrien des Krümmungstensors, dh bei jedem Tensor, der die obigen Identitäten erfüllt, kann man irgendwann eine Riemannsche Mannigfaltigkeit mit einem solchen Krümmungstensor finden. Einfache Rechnungen zeigen, dass ein solcher Tensor unabhängige Komponenten hat. Daraus folgt die Austauschsymmetrie. Die algebraischen Symmetrien sind auch äquivalent zu der Aussage, dass R zum Bild des Young-Symmetrierers gehört, der der Partition 2+2 entspricht. ${\displaystyle n^{2}\left(n^{2}-1\right)/12}$

Auf einer Riemannschen Mannigfaltigkeit hat man die kovariante Ableitung und die Bianchi-Identität (oft als zweite Bianchi-Identität oder differentielle Bianchi-Identität bezeichnet) nimmt die Form der letzten Identität in der Tabelle an. ${\displaystyle \nabla_{u}R}$

Ricci-Krümmung

Der Ricci-Krümmungstensor ist die Kontraktion des ersten und dritten Indexes des Riemann-Tensors.

${\displaystyle \underbrace {R_{ab}} _{\text{Ricci}}\equiv \underbrace {R^{c}{}_{acb}} _{\text{Riemann}}=g^{cd} \underbrace {R_{cadb}} _{\text{Riemann}}}$

Sonderfälle

Oberflächen

Für eine zweidimensionale Fläche implizieren die Bianchi-Identitäten, dass der Riemann-Tensor nur eine unabhängige Komponente hat, was bedeutet, dass der Ricci-Skalar den Riemann-Tensor vollständig bestimmt. Es gibt nur einen gültigen Ausdruck für den Riemann-Tensor, der zu den geforderten Symmetrien passt:

${\displaystyle R_{abcd}=f(R)\left(g_{ac}g_{db}-g_{ad}g_{cb}\right)}$

und durch zweimaliges Kontrahieren mit der Metrik finden wir die explizite Form:

${\displaystyle R_{abcd}=K\left(g_{ac}g_{db}-g_{ad}g_{cb}\right),}$

wobei ist der metrische Tensor und eine Funktion namens Gaußsche Krümmung und a , b , c und d nehmen entweder die Werte 1 oder 2 an. Der Riemann-Tensor hat nur eine funktional unabhängige Komponente. Die Gaußsche Krümmung fällt mit der Schnittkrümmung der Oberfläche zusammen. Es ist auch genau die Hälfte der skalaren Krümmung der 2-Mannigfaltigkeit, während der Ricci-Krümmungstensor der Fläche einfach gegeben ist durch ${\displaystyle g_{ab}}$${\displaystyle K=R/2}$

${\displaystyle R_{ab}=Kg_{ab}.}$

Raumformen

Eine Riemannsche Mannigfaltigkeit ist eine Raumform, wenn ihre Schnittkrümmung gleich einer Konstanten K ist . Der Riemann-Tensor einer Raumform ist gegeben durch

${\displaystyle R_{abcd}=K\left(g_{ac}g_{db}-g_{ad}g_{cb}\right).}$

Umgekehrt, außer in Dimension 2, wenn die Krümmung einer Riemannschen Mannigfaltigkeit diese Form für eine Funktion K hat , dann implizieren die Bianchi-Identitäten, dass K konstant ist und somit die Mannigfaltigkeit (lokal) eine Raumform ist.

Siehe auch

• Einführung in die Mathematik der Allgemeinen Relativitätstheorie
• Zerlegung des Riemannschen Krümmungstensors
• Krümmung Riemannscher Mannigfaltigkeiten
• Ricci Krümmungstensor

Zitate

Verweise