Binärer GCD-Algorithmus - Binary GCD algorithm

Visualisierung der Verwendung des binären GCD-Algorithmus, um den größten gemeinsamen Teiler (GCD) von 36 und 24 zu finden. Somit ist der GCD 2 2 × 3 = 12.

Der binäre GCD-Algorithmus , auch bekannt als Stein-Algorithmus oder binärer euklidischer Algorithmus , ist ein Algorithmus, der den größten gemeinsamen Teiler von zwei nichtnegativen ganzen Zahlen berechnet . Der Algorithmus von Stein verwendet einfachere arithmetische Operationen als der herkömmliche euklidische Algorithmus ; es ersetzt Division durch arithmetische Verschiebungen , Vergleiche und Subtraktion.

Obwohl der Algorithmus in seiner heutigen Form erstmals 1967 vom israelischen Physiker und Programmierer Josef Stein veröffentlicht wurde, war er möglicherweise im 2. Jahrhundert v. Chr. Im alten China bekannt.

Algorithmus

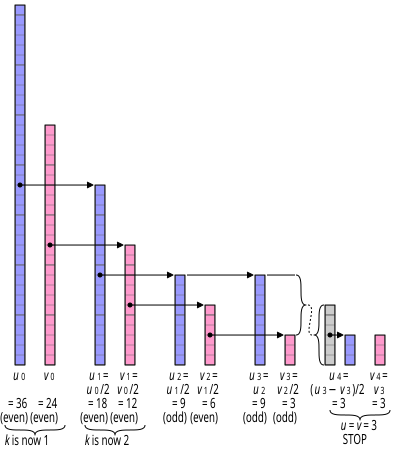
Der Algorithmus reduziert das Problem, die GCD von zwei nichtnegativen Zahlen v und u zu finden, indem er diese Identitäten wiederholt anwendet:

  • gcd(0, v ) = v , weil alles Null teilt und v die größte Zahl ist, die v teilt . Ebenso gilt gcd( u , 0) =  u .
  • gcd( 2u ,  2v ) = 2·gcd( u , v )
  • gcd( 2u ,  v ) = gcd( u ,  v ), wenn v ungerade ist (2 ist kein gemeinsamer Teiler). Ebenso gilt gcd( u ,  2v ) = gcd( u ,  v ), wenn u ungerade ist.
  • gcd( u ,  v ) = gcd(| u  −  v |, min( u , v )), wenn u und v beide ungerade sind.

Implementierung

Während die obige Beschreibung des Algorithmus mathematisch korrekt ist, unterscheiden sich performante Softwareimplementierungen typischerweise in einigen bemerkenswerten Punkten davon:

  • Verzicht auf eine Probedivision durch 2 zugunsten einer einzelnen Bitverschiebung und des Grundelements mit nachgestellten Nullen der Zählung ; dies ist funktionell äquivalent zum wiederholten Anwenden von Identität 3, aber viel schneller;
  • Ausdruck des Algorithmus iterativ statt rekursiv : Die resultierende Implementierung kann so ausgelegt werden, dass wiederholte Arbeit vermieden wird, wobei die Identität 2 am Anfang aufgerufen wird und als invariant beibehalten wird, dass beide Zahlen beim Eintritt in die Schleife ungerade sind, die nur die Identitäten 3 und 4 implementieren muss;
  • den Schleifenkörper mit Ausnahme der Ausgangsbedingung ( v == 0 ) verzweigungsfrei machen : Im folgenden Beispiel wird der Austausch von u und v (wobei u v sichergestellt wird ) zu bedingten Bewegungen kompiliert ; schwer vorhersehbare Verzweigungen können einen großen negativen Einfluss auf die Leistung haben.

Es folgt eine Implementierung des Algorithmus in Rust, die diese Unterschiede veranschaulicht, angepasst von uutils : 

pub fn gcd(mut u: u64, mut v: u64) -> u64 {
    use std::cmp::min;
    use std::mem::swap;

    // Base cases: gcd(n, 0) = gcd(0, n) = n
    if u == 0 {
        return v;
    } else if v == 0 {
        return u;
    }

    // Using identities 2 and 3:
    // gcd(2ⁱ u, 2ʲ v) = 2ᵏ gcd(u, v) with u, v odd and k = min(i, j)
    // 2ᵏ is the greatest power of two that divides both u and v
    let i = u.trailing_zeros();  u >>= i;
    let j = v.trailing_zeros();  v >>= j;
    let k = min(i, j);

    loop {
        // u and v are odd at the start of the loop
        debug_assert!(u % 2 == 1, "u = {} is even", u);
        debug_assert!(v % 2 == 1, "v = {} is even", v);

        // Swap if necessary so u <= v
        if u > v {
            swap(&mut u, &mut v);
        }

        // Using identity 4 (gcd(u, v) = gcd(|v-u|, min(u, v))
        v -= u;

        // Identity 1: gcd(u, 0) = u
        // The shift by k is necessary to add back the 2ᵏ factor that was removed before the loop
        if v == 0 {
            return u << k;
        }

        // Identity 3: gcd(u, 2ʲ v) = gcd(u, v) (u is known to be odd)
        v >>= v.trailing_zeros();
    }
}

Effizienz

Der Algorithmus erfordert O ( n ) Schritte, wobei n die Anzahl der Bits in der größeren der beiden Zahlen ist, da alle 2 Schritte mindestens einen der Operanden um mindestens den Faktor 2 reduzieren. Jeder Schritt umfasst nur wenige Arithmetik Operationen (O(1) mit kleiner Konstante); Beim Arbeiten mit wortgroßen Zahlen wird jede arithmetische Operation in eine einzelne Maschinenoperation übersetzt, so dass die Anzahl der Maschinenoperationen in der Größenordnung von log₂(max( u , v )), dh n liegt .

Die asymptotische Komplexität dieses Algorithmus beträgt jedoch O(n 2 ), da diese arithmetischen Operationen (Subtrahieren und Verschieben) jeweils lineare Zeit für beliebig große Zahlen benötigen (eine Maschinenoperation pro Wort der Darstellung). Dies ist das gleiche wie für den euklidischen Algorithmus, obwohl eine genauere Analyse von Akhavi und Vallée bewies, dass die binäre GCD etwa 60 % weniger Bitoperationen verwendet.

Erweiterungen

Der binäre GCD-Algorithmus kann auf verschiedene Weise erweitert werden, entweder um zusätzliche Informationen auszugeben, mit beliebig großen ganzen Zahlen effizienter umzugehen oder um GCDs in anderen Domänen als den ganzen Zahlen zu berechnen.

Der erweiterten binäre GGT - Algorithmus, analog zu dem erweiterten Euklidischen Algorithmus , paßt in der ersten Art von Erweiterung, da sie die liefert Bézout Koeffizienten zusätzlich zu der GCD, also ganze Zahlen a und b , so daß a · u + b · v = gcd ( u , v ).

Bei großen ganzen Zahlen ist die beste asymptotische Komplexität O (log n M( n )), wobei M( n ) die Kosten der n- Bit-Multiplikation beträgt; dies ist nahezu linear und sehr viel kleiner als O(n 2 ) des binären GCD-Algorithmus, obwohl konkrete Implementierungen ältere Algorithmen nur für Zahlen größer als etwa 64 Kilobit ( dh größer als 8 × 10 19265 ) übertreffen . Dies wird erreicht, indem der binäre GCD-Algorithmus unter Verwendung von Ideen aus dem Schönhage-Strassen-Algorithmus für eine schnelle ganzzahlige Multiplikation erweitert wird.

Der binäre GCD-Algorithmus wurde auch auf andere Bereiche als natürliche Zahlen erweitert, wie zum Beispiel Gaußsche ganze Zahlen , Eisenstein-Zahlen , quadratische Ringe und beliebige eindeutige Faktorisierungsbereiche .

Historische Beschreibung

Ein Algorithmus zur Berechnung der GCD von zwei Zahlen war im alten China unter der Han-Dynastie als Methode zur Reduzierung von Brüchen bekannt:

Wenn möglich halbieren; andernfalls nimm den Nenner und den Zähler, ziehe den kleineren vom größeren ab und mache das abwechselnd, um sie gleich zu machen. Reduzieren Sie um dieselbe Zahl.

—  Fangtian - Landvermessung, Die neun Kapitel über die mathematische Kunst

Der Satz "möglichst halbieren" ist mehrdeutig,

  • trifft dies zu, wenn eine der Zahlen gerade wird, ist der Algorithmus der binäre GCD-Algorithmus;
  • trifft dies nur zu, wenn beide Zahlen gerade sind, ähnelt der Algorithmus dem euklidischen Algorithmus .

Siehe auch

Verweise

  1. ^ Brent, Richard P. (13.–15. September 1999). Zwanzig Jahre Analyse des binären euklidischen Algorithmus . 1999 Oxford-Microsoft Symposium zu Ehren von Professor Sir Antony Hoare. Oxford.
  2. ^ Brent, Richard P. (November 1999). Weitere Analyse des binären euklidischen Algorithmus (Technischer Bericht). Computerlabor der Universität Oxford. arXiv : 1303.2772 . PRG TR-7-99.
  3. ^ Stein, J. (Februar 1967), "Computational Probleme im Zusammenhang mit Racah Algebra", Journal of Computational Physics , 1 (3): 397–405, Bibcode : 1967JCoPh...1..397S , doi : 10.1016/0021- 9991(67)90047-2 , ISSN  0021-9991
  4. ^ a b Knuth, Donald (1998), Seminumerical Algorithms , The Art of Computer Programming , 2 (3. Aufl.), Addison-Wesley, ISBN 978-0-201-89684-8
  5. ^ a b Zhang, Shaohua (2009-10-05). „Das Konzept der Primzahlen und der Algorithmus zum Zählen des größten gemeinsamen Teilers im alten China“. arXiv : 0910.0095 [ math.HO ].
  6. ^ Gottbolzen, Matt. "Compiler-Explorer" . Abgerufen am 10. Juli 2021 .
  7. ^ Kapoor, Rajiv (2009-02-21). "Vermeidung der Kosten von Fehlprognosen in der Filiale" . Intel-Entwicklerzone .
  8. ^ Lemire, Daniel (2019-10-15). "Fehlvorhergesagte Filialen können Ihre Laufzeiten vervielfachen" .
  9. ^ "GNU MP 6.1.2: Binäres GCD" .
  10. ^ Akhavi, Ali; Vallée, Brigitte (2000), "Average Bit-Complexity of Euclidean Algorithms" , Proceedings ICALP'00, Lecture Notes Computer Science 1853 : 373–387, CiteSeerX  10.1.1.42.7616
  11. ^ Knuth 1998 , p. 646, Antwort auf Übung 39 von Abschnitt 4.5.2
  12. ^ Menezes, Alfred J.; van Oorschot, Paul C.; Vanstone, Scott A. (Oktober 1996). "§14.4 Greatest Common Divisor Algorithmen" (PDF) . Handbuch der Angewandten Kryptographie . CRC-Presse. S. 606–610. ISBN 0-8493-8523-7. Abgerufen 2017-09-09 .
  13. ^ Cohen, Henri (1993). "Kapitel 1: Grundlegende zahlentheoretische Algorithmen". Ein Kurs in computergestützter algebraischer Zahlentheorie . Abschlusstexte der Mathematik . 138 . Springer-Verlag . S. 17–18. ISBN 0-387-55640-0.
  14. ^ Stehlé, Damien; Zimmermann, Paul (2004), "Ein binärer rekursiver gcd-Algorithmus" (PDF) , Algorithmische Zahlentheorie , Vorlesungsnotizen in Comput. Sci., 3076 , Springer, Berlin, S. 411–425, CiteSeerX  10.1.1.107.8612 , doi : 10.1007/978-3-540-24847-7_31 , ISBN 978-3-540-22156-2, MR  2138011 , INRIA Forschungsbericht RR-5050.
  15. ^ Weilert, André (Juli 2000). "(1+i)-ary GCD Computation in Z[i] as a Analogue to the Binary GCD Algorithm" . Zeitschrift für symbolische Berechnung . 30 (5): 605–617. doi : 10.1006/jsco.2000.0422 .
  16. ^ Damgård, Ivan Bjerre; Frandsen, Gudmund Skovbjerg (12.–15. August 2003). Effiziente Algorithmen für GCD und kubische Reste im Ring der Eisenstein-Ganzzahlen . 14. Internationales Symposium zu den Grundlagen der Computertheorie. Malmö , Schweden . S. 109–117. doi : 10.1007/978-3-540-45077-1_11 .CS1-Wartung: Datumsformat ( Link )
  17. ^ Agarwal, Saurabh; Frandsen, Gudmund Skovbjerg (13.–18. Juni 2004). Binäre GCD-ähnliche Algorithmen für einige komplexe quadratische Ringe . Symposium zur Algorithmischen Zahlentheorie. Burlington, VT , USA. S. 57–71. doi : 10.1007/978-3-540-24847-7_4 .CS1-Wartung: Datumsformat ( Link )
  18. ^ Agarwal, Saurabh; Frandsen, Gudmund Skovbjerg (20.–24. März 2006). Ein neuer GCD-Algorithmus für quadratische Zahlenringe mit eindeutiger Faktorisierung . 7. Lateinamerikanisches Symposium für Theoretische Informatik. Valdivia, Chile . S. 30–42. doi : 10.1007/11682462_8 .CS1-Wartung: Datumsformat ( Link )
  19. ^ Wikström, Douglas (11.–15. Juli 2005). Zum l-Ary GCD-Algorithmus in Rings of Integers . Automaten, Sprachen und Programmierung, 32. Internationales Kolloquium. Lissabon , Portugal . S. 1189–1201. doi : 10.1007/11523468_96 .CS1-Wartung: Datumsformat ( Link )

Weiterlesen

Behandelt die erweiterte binäre GCD und eine probabilistische Analyse des Algorithmus.

Behandelt eine Vielzahl von Themen, einschließlich des erweiterten binären GCD-Algorithmus, der Bézout-Koeffizienten ausgibt , die effiziente Handhabung von ganzen Zahlen mit Mehrfachpräzision unter Verwendung einer Variante des GCD-Algorithmus von Lehmer und die Beziehung zwischen GCD und Kettenbruchentwicklungen reeller Zahlen.

Eine Analyse des Algorithmus im durchschnittlichen Fall durch die Linse der Funktionsanalyse : Die Hauptparameter des Algorithmus werden als dynamisches System dargestellt , und ihr Durchschnittswert wird mit dem invarianten Maß des Transferoperators des Systems in Beziehung gesetzt .

Externe Links