Dyadisch rational - Dyadic rational

Dyadische rationale Zahlen im Intervall von 0 bis 1

In der Mathematik ist eine dyadische oder binäre rationale Zahl eine Zahl, die als Bruch ausgedrückt werden kann, deren Nenner eine Zweierpotenz ist . 1/2, 3/2 und 3/8 sind beispielsweise dyadische rationale Zahlen, 1/3 jedoch nicht. Diese Zahlen sind in der Informatik wichtig, weil sie die einzigen mit endlicher binärer Darstellung sind . Dyadische Rationale haben auch Anwendungen in Gewichten und Maßen, musikalischen Taktarten und in der frühen Mathematikausbildung. Sie können jede reelle Zahl genau annähern .

Die Summe, Differenz oder das Produkt zweier dyadischer rationaler Zahlen ist eine weitere dyadische rationale Zahl, die durch eine einfache Formel gegeben ist. Die Division einer dyadischen rationalen Zahl durch eine andere führt jedoch nicht immer zu einem dyadischen rationalen Ergebnis. Mathematisch bedeutet dies, dass die dyadischen rationalen Zahlen einen Ring bilden , der zwischen dem Ring der ganzen Zahlen und dem Körper der rationalen Zahlen liegt . Dieser Ring kann bezeichnet werden . ${\displaystyle \mathbb{Z} [{\tfrac {1}{2}}]}$

In der fortgeschrittenen Mathematik sind die dyadischen rationalen Zahlen von zentraler Bedeutung für die Konstruktionen des dyadischen Solenoids , der Minkowski-Fragezeichenfunktion , der Daubechies-Wavelets , der Thompsons-Gruppe , der Prüfer-2-Gruppe , der surrealen Zahlen und der schmelzbaren Zahlen . Diese Zahlen sind ordnungsisomorph zu den rationalen Zahlen; sie bilden ein Untersystem der 2-adischen Zahlen sowie der reellen Zahlen und können die Bruchteile von 2-adischen Zahlen darstellen. Funktionen von natürlichen Zahlen bis hin zu dyadischen rationalen Zahlen wurden verwendet, um die mathematische Analyse in der umgekehrten Mathematik zu formalisieren .

Anwendungen

In Messung

Küchengewichte mit dyadischen Bruchteilen eines Pfunds von 2 lb bis 1/64 lb (1/4 oz)

Viele traditionelle Gewichts- und Maßsysteme basieren auf der Idee der wiederholten Halbierung, die bei der Messung von Bruchteilen von Einheiten zu dyadischen Rationalitäten führt. Der Zoll wird normalerweise in dyadische rationale Zahlen unterteilt, anstatt eine dezimale Unterteilung zu verwenden. Die üblichen Einteilungen der Gallone in halbe Gallonen, Quarts , Pints und Cups sind ebenfalls dyadisch. Die alten Ägypter verwendeten bei der Messung dyadische Rationale mit Nennern bis 64. Ähnlich basieren Gewichtssysteme aus der Industal-Zivilisation größtenteils auf wiederholter Halbierung; Anthropologin Heather M.-L. Miller schreibt, dass "das Halbieren bei Balkenwaagen eine relativ einfache Operation ist, weshalb wahrscheinlich so viele Gewichtssysteme dieser Zeit binäre Systeme verwendeten".

Im Computerbereich

Dyadische Rationale sind als eine Art von Bruchzahl, die viele Computer direkt manipulieren können, von zentraler Bedeutung für die Informatik . Insbesondere Gleitkommazahlen werden als von Computern verwendeter Datentyp oft als ganze Zahlen multipliziert mit positiven oder negativen Zweierpotenzen definiert. Die Zahlen, die in einem Gleitkommaformat genau dargestellt werden können, wie die IEEE-Gleitkomma-Datentypen , werden als darstellbare Zahlen bezeichnet. Bei den meisten Gleitkommadarstellungen sind die darstellbaren Zahlen eine Teilmenge der dyadischen rationalen Zahlen. Das gleiche gilt für Festkomma-Datentypen , die in den meisten Fällen auch implizit Zweierpotenzen verwenden. Wegen der Einfachheit des Rechnens mit dyadischen Rationalen werden sie auch für exakte reelle Berechnungen mit Intervallarithmetik verwendet und sind für einige theoretische Modelle berechenbarer Zahlen von zentraler Bedeutung .

Die Erzeugung einer Zufallsvariablen aus Zufallsbits in einer festen Zeitdauer ist nur möglich, wenn die Variable endlich viele Ergebnisse hat, deren Wahrscheinlichkeiten alle dyadische rationale Zahlen sind. Für Zufallsvariablen, deren Wahrscheinlichkeiten nicht dyadisch sind, ist es notwendig, ihre Wahrscheinlichkeiten entweder durch dyadische Rationale zu approximieren oder einen zufälligen Erzeugungsprozess zu verwenden, dessen Zeit selbst zufällig und unbeschränkt ist.

In Musik

Fünf Bars von Igor Stravinski ‚s The Rite of Spring
zeigt Taktartbezeichnungen³
₁₆, ²
₁₆, ³
₁₆, und ²
₈

Taktarten in der westlichen Musiknotation werden traditionell in einer Form geschrieben, die Brüchen ähnelt (zum Beispiel:²
₂, ⁴
₄, oder ⁶
₈), obwohl die horizontale Linie der Notenzeile, die die obere und untere Zahl trennt, normalerweise weggelassen wird, wenn die Signatur getrennt von ihrer Notenzeile geschrieben wird. Als Brüche sind sie im Allgemeinen dyadisch, obwohl auch nicht-dyadische Taktarten verwendet wurden. Der als Bruch interpretierte numerische Wert der Signatur beschreibt die Länge eines Taktes als Bruch einer ganzen Note . Sein Zähler beschreibt die Anzahl der Schläge pro Takt und der Nenner beschreibt die Länge jedes Schlags.

Im Mathematikunterricht

In Theorien der kindlichen Entwicklung des Konzepts eines Bruchs, die auf der Arbeit von Jean Piaget basieren , gehören Bruchzahlen, die durch Halbieren und wiederholtes Halbieren entstehen, zu den frühesten Formen von Brüchen, die sich entwickeln. Diese Entwicklungsstufe des Konzepts der Brüche wurde als "algorithmische Halbierung" bezeichnet. Die Addition und Subtraktion dieser Zahlen kann in Schritten durchgeführt werden, die nur das Verdoppeln, Halbieren, Addieren und Subtrahieren von ganzen Zahlen beinhalten. Im Gegensatz dazu beinhaltet die Addition und Subtraktion von allgemeineren Brüchen eine ganzzahlige Multiplikation und Faktorisierung, um einen gemeinsamen Nenner zu erreichen. Daher können die Schüler mit dyadischen Brüchen leichter rechnen als mit allgemeineren Brüchen.

Definitionen und Arithmetik

Die dyadischen Zahlen sind die rationalen Zahlen , die sich aus der Division einer ganzen Zahl durch eine Zweierpotenz ergeben . Eine rationale Zahl ist im einfachsten Sinne eine dyadische rationale Zahl, wenn sie eine Zweierpotenz ist. Eine andere äquivalente Art, die dyadischen rationalen Zahlen zu definieren, besteht darin, dass sie die reellen Zahlen sind , die eine abschließende binäre Darstellung haben . ${\displaystyle p/q}$${\displaystyle q}$

Addition , Subtraktion und Multiplikation von zwei beliebigen dyadischen Rationalen ergibt ein weiteres dyadisches Rational gemäß den folgenden Formeln:

${\displaystyle {\begin{ausgerichtet}{\frac {a}{2^{b}}}+{\frac {c}{2^{d}}}&={\frac {2^{d-\ min(b,d)}a+2^{b-\min(b,d)}c}{2^{\max(b,d)}}}\\[6px]{\frac {a}{ 2^{b}}}-{\frac {c}{2^{d}}}&={\frac {2^{d-\min(b,d)}a-2^{b-\min (b,d)}c}{2^{\max(b,d)}}}\\[6px]{\frac {a}{2^{b}}}\cdot {\frac {c}{ 2^{d}}}&={\frac {ac}{2^{b+d}}}\end{ausgerichtet}}}$

Das Ergebnis der Division einer dyadischen Rationalität durch eine andere ist jedoch nicht unbedingt eine dyadische Rationale. Zum Beispiel sind 1 und 3 beide dyadische rationale Zahlen, aber 1/3 nicht.

Zusätzliche Eigenschaften

Dyadische rationale Approximationen an die Quadratwurzel von 2 ( ), gefunden durch Runden auf das nächste kleinere ganzzahlige Vielfache von für Die Höhe des rosa Bereichs über jeder Approximation ist ihr Fehler.${\displaystyle {\sqrt {2}}\approx 1,4142}$${\displaystyle 1/2^{i}}$${\displaystyle i=0,1,2,\dots}$

Reelle Zahlen ohne ungewöhnlich genaue dyadische rationale Approximationen. Die roten Kreise umgeben Zahlen, die innerhalb des Fehlers durch angenähert werden . Für Zahlen im fraktalen Cantor außerhalb der Kreise haben alle dyadischen rationalen Approximationen größere Fehler.${\displaystyle {\tfrac {1}{6}}/2^{i}}$${\displaystyle n/2^{i}}$

Jede ganze Zahl und jede halbe ganze Zahl ist ein dyadisches Rational. Beide erfüllen die Definition einer Ganzzahl geteilt durch eine Zweierpotenz: Jede Ganzzahl ist eine Ganzzahl geteilt durch Eins (die nullte Zweierpotenz), und jede halbe Ganzzahl ist eine Ganzzahl geteilt durch zwei.

Jede reelle Zahl kann durch dyadische rationale Zahlen beliebig eng angenähert werden. Betrachten Sie insbesondere für eine reelle Zahl die dyadischen Rationalen der Form , wobei kann eine beliebige ganze Zahl sein und bezeichnet die Bodenfunktion , die ihr Argument auf eine ganze Zahl abrundet. Diese Zahlen nähern sich von unten bis auf einen Fehler von , der beliebig klein gemacht werden kann, indem beliebig groß gewählt wird. Für eine fraktale Teilmenge der reellen Zahlen liegt diese Fehlergrenze innerhalb eines konstanten optimalen Faktors: Für diese Zahlen gibt es keine Approximation mit einem Fehler kleiner als eine Konstante mal . Die Existenz genauer dyadischer Approximationen kann dadurch ausgedrückt werden, dass die Menge aller dyadischen rationalen Zahlen dicht in der reellen Linie ist . Noch stärker ist, dass diese Menge gleichmäßig dicht ist, in dem Sinne, dass die dyadischen rationalen Zahlen mit Nenner gleichmäßig auf der reellen Linie verteilt sind. ${\displaystyle x}$${\textstyle \lfloor 2^{i}x\rfloor /2^{i}}$${\displaystyle i}$${\displaystyle \lfloor \dots \rfloor}$${\displaystyle x}$${\displaystyle 1/2^{i}}$${\displaystyle i}$${\displaystyle n/2^{i}}$${\displaystyle 1/2^{i}}$${\displaystyle 2^{i}}$

Die dyadischen rationalen Zahlen sind genau die Zahlen, die endliche binäre Erweiterungen besitzen . Ihre binären Erweiterungen sind nicht eindeutig; es gibt eine endliche und eine unendliche Darstellung jedes dyadischen Rationalen außer 0 (ohne Berücksichtigung der terminalen Nullen). Zum Beispiel 0,11 ₂ = 0,10111... ₂ , was zwei verschiedene Darstellungen für 3/4 ergibt. Die dyadischen rationalen Zahlen sind die einzigen Zahlen, deren Binärentwicklungen nicht eindeutig sind.

In fortgeschrittener Mathematik

Algebraische Struktur

Da sie durch Addition, Subtraktion und Multiplikation, aber nicht durch Division abgeschlossen sind, sind die dyadischen rationalen Zahlen ein Ring, aber kein Körper . Der Ring der dyadischen rationalen Zahlen kann mit bezeichnet werden , was bedeutet, dass er durch Auswertung von Polynomen mit ganzzahligen Koeffizienten am Argument 1/2 erzeugt werden kann. Als Ring sind die dyadischen rationalen Zahlen ein Unterring der rationalen Zahlen und ein Überring der ganzen Zahlen. Algebraisch ist dieser Ring die Lokalisierung der ganzen Zahlen in Bezug auf die Menge der Zweierpotenzen . ${\displaystyle \mathbb{Z} [{\tfrac {1}{2}}]}$

Die dyadischen rationalen Zahlen bilden nicht nur einen Teilring der reellen Zahlen , sondern auch einen Teilring der 2-adischen Zahlen , ein Zahlensystem, das aus Binärdarstellungen definiert werden kann, die rechts vom Binärpunkt endlich sind, sich aber unendlich erstrecken können weit nach links. Die 2-adischen Zahlen umfassen alle rationalen Zahlen, nicht nur die dyadischen rationalen Zahlen. Die Einbettung der dyadischen Rationalen in die 2-adischen Zahlen ändert nichts an der Arithmetik der dyadischen Rationalen, aber es gibt ihnen eine andere topologische Struktur als sie als Teilring der reellen Zahlen haben. Wie in den reellen Zahlen bilden die dyadischen rationalen Zahlen eine dichte Teilmenge der 2-adischen Zahlen und sind die Menge der 2-adischen Zahlen mit endlichen binären Erweiterungen. Jede 2-adische Zahl kann in die Summe einer 2-adischen ganzen Zahl und einer dyadischen rationalen Zahl zerlegt werden; in diesem Sinne können die dyadischen rationalen Zahlen die Bruchteile von 2-adischen Zahlen darstellen, aber diese Zerlegung ist nicht eindeutig.

Die Addition der dyadischen Rationalen modulo 1 (der Quotientengruppe der dyadischen Rationalen durch die ganzen Zahlen) bildet die Prüfer 2-Gruppe . ${\displaystyle \mathbb {Z} [{\tfrac {1}{2}}]/\mathbb {Z} }$

Dyadischer Magnet

Betrachtet man nur die Additions- und Subtraktionsoperationen der dyadischen rationalen Zahlen, so erhalten sie die Struktur einer additiven abelschen Gruppe . Die Pontryagin-Dualität ist eine Methode zum Verständnis abelscher Gruppen durch Konstruktion dualer Gruppen, deren Elemente Charaktere der ursprünglichen Gruppe sind, Gruppenhomomorphismen zur multiplikativen Gruppe der komplexen Zahlen , mit punktweiser Multiplikation als dualer Gruppenoperation. Die so konstruierte duale Gruppe der additiven dyadischen Rationale kann auch als topologische Gruppe angesehen werden . Es wird dyadischer Solenoid genannt und ist isomorph zum topologischen Produkt der reellen Zahlen und 2-adischen Zahlen, quotiert durch die diagonale Einbettung der dyadischen rationalen Zahlen in dieses Produkt. Es ist ein Beispiel für einen Protorus , ein Solenoid und ein unzerlegbares Kontinuum .

Funktionen mit dyadischen rationalen Zahlen als ausgezeichnete Punkte

Die Fragezeichenfunktion von Minkowski bildet rationale Zahlen auf dyadische rationale Zahlen ab

Ein Daubechies-Wavelet , das bei dyadischen rationalen Punkten Ungleichmäßigkeiten zeigt

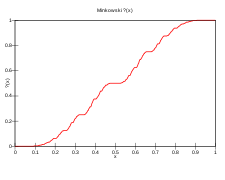
Da sie eine dichte Teilmenge der reellen Zahlen sind, bilden die dyadischen rationalen Zahlen mit ihrer numerischen Ordnung eine dichte Ordnung . Wie bei zwei beliebigen unbeschränkten abzählbaren dichten linearen Ordnungen sind nach dem Isomorphismussatz von Cantor die dyadischen Rationalen ordnungsisomorph zu den rationalen Zahlen. In diesem Fall liefert die Fragezeichenfunktion von Minkowski eine ordnungserhaltende Bijektion zwischen der Menge aller rationalen Zahlen und der Menge der dyadischen rationalen Zahlen.

Die dyadischen Rationale spielen eine Schlüsselrolle bei der Analyse von Daubechies-Wavelets , da die Menge von Punkten, an denen die Skalierungsfunktion dieser Wavelets nicht glatt ist. In ähnlicher Weise parametrisieren die dyadischen Rationalen die Diskontinuitäten in der Grenze zwischen stabilen und instabilen Punkten im Parameterraum der Hénon-Abbildung .

Die Menge der stückweise linearen Homöomorphismen vom Einheitsintervall zu sich selbst, die Steigungen der Potenz von 2 und dyadisch-rationale Bruchpunkte aufweisen, bildet eine Gruppe unter der Operation der Funktionskomposition . Dies ist Thompsons Gruppe , das erste bekannte Beispiel einer unendlichen, aber endlich präsentierten einfachen Gruppe . Dieselbe Gruppe kann auch durch eine Aktion auf verwurzelte Binärbäume oder durch eine Aktion auf die dyadischen Rationalen innerhalb des Einheitsintervalls repräsentiert werden.

Andere verwandte Konstruktionen

In der umgekehrten Mathematik besteht eine Möglichkeit, die reellen Zahlen zu konstruieren, darin, sie als Funktionen von unären Zahlen bis zu dyadischen rationalen Zahlen darzustellen , wobei der Wert einer dieser Funktionen für das Argument ein dyadischer rationaler Wert mit einem Nenner ist , der sich der gegebenen reellen Zahl annähert. Die Definition reeller Zahlen auf diese Weise ermöglicht den Nachweis vieler grundlegender Ergebnisse der mathematischen Analysis innerhalb einer eingeschränkten Theorie der Arithmetik zweiter Ordnung, die als "feasible analysis" (BTFA) bezeichnet wird. ${\displaystyle i}$${\displaystyle 2^{i}}$

Die surrealen Zahlen werden durch ein iteriertes Konstruktionsprinzip erzeugt, das mit der Erzeugung aller endlichen dyadischen rationalen Zahlen beginnt und dann fortfährt, neue und seltsame Arten von unendlichen, infinitesimalen und anderen Zahlen zu erzeugen. Dieses Zahlensystem ist die Grundlage für die kombinatorische Spieltheorie , und dyadische Rationale treten in dieser Theorie natürlicherweise als Menge von Werten bestimmter kombinatorischer Spiele auf.

Die schmelzbaren Zahlen sind eine Teilmenge der dyadischen rationalen Zahlen , der Abschluss der Menge unter der Operation , beschränkt auf Paare mit . Sie sind wohlgeordnet , wobei der Auftragstyp der Epsilon-Zahl entspricht . Für jede ganze Zahl hat die kleinste schmelzbare Zahl, die größer als ist, die Form . Die Existenz von für jede kann in der Peano-Arithmetik nicht bewiesen werden und wächst so schnell als Funktion davon , denn sie ist (in Knuths Aufwärtspfeil-Notation für große Zahlen) bereits größer als . ${\displaystyle \{0\}}$${\displaystyle x,y\mapsto (x+y+1)/2}$${\displaystyle x,y}$${\displaystyle |xy|<1}$ ${\displaystyle \varepsilon_{0}}$${\displaystyle n}$${\displaystyle n}$${\displaystyle n+1/2^{k}}$${\displaystyle k}$${\displaystyle n}$${\displaystyle k}$${\displaystyle n}$${\displaystyle n=3}$${\displaystyle 2\uparrow ^{9}16}$

Verweise