Kantorensatz - Cantor set

In der Mathematik ist die Cantor-Menge eine Menge von Punkten, die auf einem einzelnen Liniensegment liegen und eine Reihe von nicht intuitiven Eigenschaften aufweisen. Es wurde 1874 von Henry John Stephen Smith entdeckt und 1883 vom deutschen Mathematiker Georg Cantor eingeführt .

Durch die Berücksichtigung dieser Menge halfen Cantor und andere, die Grundlagen der modernen Punktmengentopologie zu legen . Obwohl Cantor selbst die Menge auf allgemeine, abstrakte Weise definierte, ist die gebräuchlichste moderne Konstruktion die Cantor ternäre Menge , die durch Entfernen des mittleren Drittels eines Liniensegments und anschließendes Wiederholen des Vorgangs mit den verbleibenden kürzeren Segmenten erstellt wird. Cantor selbst erwähnte die ternäre Konstruktion nur am Rande, als Beispiel für eine allgemeinere Idee, die einer perfekten Menge , die nirgendwo dicht ist .

Vergrößern Sie das Cantor-Set. Jeder Punkt in der Menge wird hier durch eine vertikale Linie dargestellt.

Aufbau und Formel der ternären Menge

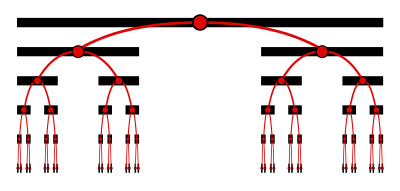
Die ternäre Menge von Cantor wird durch iteratives Löschen des offenen mittleren Drittels aus einer Reihe von Liniensegmenten erstellt. Man beginnt damit, das offene mittlere Drittel aus dem Intervall zu streichen , so dass zwei Liniensegmente übrig bleiben: . Als nächstes wird das offene mittlere Drittel jedes dieser verbleibenden Segmente gelöscht, so dass vier Liniensegmente übrig bleiben: . Dieser Prozess wird endlos fortgesetzt , wobei die n- te Menge ${\displaystyle {\mathcal {C}}}$${\textstyle \left({\frac {1}{3}},{\frac {2}{3}}\right)}$ ${\displaystyle \textstyle \left[0,1\right]}$${\textstyle \left[0,{\frac {1}{3}}\right]\cup \left[{\frac {2}{3}},1\right]}$${\textstyle \left[0,{\frac {1}{9}}\right]\cup \left[{\frac {2}{9}},{\frac {1}{3}}\right] \cup \left[{\frac {2}{3}},{\frac {7}{9}}\right]\cup \left[{\frac {8}{9}},1\right]}$

${\displaystyle C_{n}={\frac {C_{n-1}}{3}}\cup \left({\frac {2}{3}}+{\frac {C_{n-1}} {3}}\right){\text{ für }}n\geq 1,{\text{ und }}C_{0}=[0,1].}$

Die ternäre Menge von Cantor enthält alle Punkte im Intervall , die in keinem Schritt dieses unendlichen Prozesses gelöscht werden: ${\displaystyle [0,1]}$

${\displaystyle {\mathcal {C}}:=\bigcap_{n=0}^{\infty}C_{n}=\bigcap _{n=m}^{\infty}C_{n}}$   für jeden   ${\displaystyle m\geq 0.}$

Die ersten sechs Schritte dieses Prozesses sind unten dargestellt.

Unter Verwendung der Idee der selbstähnlichen Transformationen und der expliziten geschlossenen Formeln für die Cantor-Menge sind ${\displaystyle T_{L}(x)=x/3,T_{R}(x)=(2+x)/3}$${\displaystyle C_{n}=T_{L}(C_{n-1})\cup T_{R}(C_{n-1}),}$

${\displaystyle {\mathcal {C}}=[0,1]\,\setminus\,\bigcup_{n=0}^{\infty}\bigcup_{k=0}^{3^{n} -1}\left({\frac {3k+1}{3^{n+1}}},{\frac {3k+2}{3^{n+1}}}\right),}$

wobei jedes mittlere Drittel als offenes Intervall aus dem es umgebenden geschlossenen Intervall entfernt wird, oder ${\textstyle \left({\frac {3k+1}{3^{n+1}}},{\frac {3k+2}{3^{n+1}}}\right)}$${\textstyle \left[{\frac {3k+0}{3^{n+1}}},{\frac {3k+3}{3^{n+1}}}\right]=\left[ {\frac {k+0}{3^{n}}},{\frac {k+1}{3^{n}}}\right]}$

${\displaystyle {\mathcal {C}}=\bigcap _{n=1}^{\infty}\bigcup _{k=0}^{3^{n-1}-1}\left(\left[ {\frac {3k+0}{3^{n}}},{\frac {3k+1}{3^{n}}}\right]\cup \left[{\frac {3k+2}{ 3^{n}}},{\frac {3k+3}{3^{n}}}\right]\right),}$

wobei das mittlere Drittel des vorhergehenden geschlossenen Intervalls durch Schnitt mit entfernt wird${\textstyle \left({\frac {3k+1}{3^{n}}},{\frac {3k+2}{3^{n}}}\right)}$${\textstyle \left[{\frac {k+0}{3^{n-1}}},{\frac {k+1}{3^{n-1}}}\right]=\left[ {\frac {3k+0}{3^{n}}},{\frac {3k+3}{3^{n}}}\right]}$${\textstyle \left[{\frac {3k+0}{3^{n}}},{\frac {3k+1}{3^{n}}}\right]\cup \left[{\frac {3k+2}{3^{n}}},{\frac {3k+3}{3^{n}}}\right].}$

Dieser Vorgang des Entfernens der mittleren Drittel ist ein einfaches Beispiel für eine endliche Unterteilungsregel . Die ternäre Menge von Cantor ist ein Beispiel für einen fraktalen String .

Rechnerisch besteht die Cantor-Menge aus allen reellen Zahlen des Einheitsintervalls , die die Ziffer 1 nicht benötigen, um als ternärer (Basis 3) Bruch ausgedrückt zu werden . Wie das obige Diagramm veranschaulicht, wird jeder Punkt in der Cantor-Menge eindeutig durch einen Pfad durch einen unendlich tiefen Binärbaum lokalisiert, wobei der Pfad auf jeder Ebene nach links oder rechts abbiegt, je nachdem, auf welcher Seite eines gelöschten Segments der Punkt liegt. Stellt man jede Linkskurve mit 0 und jede Rechtskurve mit 2 dar, ergibt sich der ternäre Bruch für einen Punkt. ${\displaystyle [0,1]}$

Komposition

Da die Cantor-Menge als die Menge der nicht ausgeschlossenen Punkte definiert ist, kann der Anteil (dh das Maß ) des verbleibenden Einheitsintervalls durch die entfernte Gesamtlänge ermittelt werden. Diese Summe ist die geometrische Progression

${\displaystyle \sum _{n=0}^{\infty }{\frac {2^{n}}{3^{n+1}}}={\frac {1}{3}}+{\ frac {2}{9}}+{\frac {4}{27}}+{\frac {8}{81}}+\cdots ={\frac {1}{3}}\left({\frac {1}{1-{\frac{2}{3}}}}\right)=1.}$

Damit ist der verbleibende Anteil 1 − 1 = 0.

Diese Berechnung legt nahe, dass die Cantor-Menge kein Intervall mit einer Länge ungleich Null enthalten kann . Es mag überraschend erscheinen, dass etwas übrig bleiben sollte – schließlich ist die Summe der Längen der entfernten Intervalle gleich der Länge des ursprünglichen Intervalls. Ein genauerer Blick auf den Prozess zeigt jedoch, dass etwas übrig bleiben muss, da das Entfernen des "mittleren Drittels" jedes Intervalls das Entfernen offener Mengen (Mengen, die ihre Endpunkte nicht enthalten) beinhaltet. Entfernen Sie also das Liniensegment (1/3, 2/3) aus dem ursprünglichen Intervall [0, 1] hinterlässt die Punkte 1/3 und 2/3. Nachfolgende Schritte entfernen diese (oder andere) Endpunkte nicht, da die entfernten Intervalle immer innerhalb der verbleibenden Intervalle liegen. Die Cantor-Menge ist also nicht leer und enthält tatsächlich eine unzählbar unendliche Anzahl von Punkten (wie aus der obigen Beschreibung in Form von Pfaden in einem unendlichen Binärbaum hervorgeht).

Es kann den Anschein haben, dass nur die Endpunkte der Konstruktionssegmente übrig sind, aber auch das ist nicht der Fall. Die Nummer1/4Zum Beispiel hat die einzigartige dreiteilige Form 0.020202 ... = 0. 02 . Es befindet sich im unteren Drittel und im oberen Drittel dieses Drittels und im unteren Drittel dieses oberen Drittels und so weiter. Da es sich nie in einem der mittleren Segmente befindet, wird es nie entfernt. Er ist aber auch kein Endpunkt eines mittleren Segments, da er kein Vielfaches einer Potenz von 1/3 ist. Alle Endpunkte von Segmenten sind abschließende ternäre Brüche und sind in der Menge enthalten

${\displaystyle \left\{x\in [0,1]\mid \exists i\in\mathbb {N} _{0}:x\,3^{i}\in \mathbb {Z} \right\ }\qquad {\Bigl(}\subset\mathbb{N}_{0}\,3^{-\mathbb{N}_{0}}{\Bigr)}}$

was eine abzählbar unendliche Menge ist. Was die Kardinalität betrifft , so sind fast alle Elemente der Cantor-Menge weder Endpunkte von Intervallen noch rationale Punkte wie 1/4. Der ganze Cantor-Satz ist tatsächlich nicht zählbar.

Eigenschaften

Kardinalität

Es kann gezeigt werden, dass in diesem Prozess genauso viele Punkte zurückbleiben wie anfangs, und dass daher die Cantor-Menge überzählig ist . Um dies zu sehen, zeigen wir, dass es eine Funktion f aus der Cantor-Menge auf das abgeschlossene Intervall [0,1] gibt, die surjektiv ist (dh f bildet von auf [0,1] ab), so dass die Kardinalität von nicht kleiner ist von [0,1]. Da es sich um eine Teilmenge von [0,1] handelt, ist ihre Kardinalität auch nicht größer, sodass die beiden Kardinalitäten nach dem Satz von Cantor-Bernstein-Schröder tatsächlich gleich sein müssen . ${\displaystyle {\mathcal {C}}}$${\displaystyle {\mathcal {C}}}$${\displaystyle {\mathcal {C}}}$${\displaystyle {\mathcal {C}}}$

Um diese Funktion zu konstruieren, betrachten Sie die Punkte im [0, 1]-Intervall in Bezug auf die Notation zur Basis 3 (oder ternär ). Denken Sie daran, dass die richtigen ternären Brüche, genauer: die Elemente von , mehr als eine Darstellung in dieser Notation zulassen, wie zum Beispiel${\displaystyle {\bigl(}\mathbb{Z}\setminus\{0\}{\bigr)}\cdot 3^{-\mathbb{N}_{0}}}$1/3, die geschrieben werden kann als 0.1 ₃ = 0.1 0 ₃ , aber auch als 0.0222... ₃ = 0.0 2 ₃ , und2/3, das kann geschrieben werden als 0.2 ₃ = 0.2 0 ₃ aber auch als 0.1222... ₃ = 0.1 2 ₃ . Wenn wir das mittlere Drittel entfernen, enthält dieses die Zahlen mit ternären Ziffern der Form 0.1xxxxx... _3, wobei xxxxx... ₃ genau zwischen 00000... ₃ und 22222... _{3 liegt} . Die nach dem ersten Schritt verbleibenden Zahlen bestehen also aus

• Zahlen der Form 0.0xxxxx... ₃ (einschließlich 0.022222... ₃ = 1/3)
• Zahlen der Form 0,2xxxxx... ₃ (einschließlich 0,222222... ₃ = 1)

Dies lässt sich zusammenfassen, indem man sagt, dass diejenigen Zahlen mit einer ternären Darstellung, bei denen die erste Ziffer nach dem Wurzelpunkt nicht 1 ist, die nach dem ersten Schritt verbleibenden sind.

Der zweite Schritt entfernt Zahlen der Form 0,01xxxx... ₃ und 0,21xxxx... ₃ , und (mit entsprechender Sorgfalt für die Endpunkte) kann geschlossen werden, dass die verbleibenden Zahlen diejenigen mit einer ternären Zahl sind, wobei keine der ersten zwei Ziffern 1 ist .

Damit eine Zahl in Schritt n nicht ausgeschlossen werden kann , muss sie eine ternäre Darstellung haben, deren n- te Ziffer nicht 1 ist. Damit eine Zahl in der Cantor-Menge enthalten ist, darf sie in keinem Schritt ausgeschlossen werden, es muss eine Zifferndarstellung zulassen, die ausschließlich aus 0 und 2 besteht.

Es ist erwähnenswert, dass Zahlen wie 1 1/3= 0,1 ₃ und7/9= 0.21 ₃ sind in der Cantor-Menge, da sie ternäre Ziffern haben, die ausschließlich aus 0 und 2 bestehen: 1 = 0.222... ₃ = 0. 2 ₃ ,1/3= 0,0222... ₃ = 0,0 2 ₃ und7/9= 0,20222... ₃ = 0,20 2 ₃ . Alle letzteren Zahlen sind „Endpunkte“, und diese Beispiele sind rechte Grenzwerte von . Das gleiche gilt für die linken Grenzpunkte von , zB${\displaystyle {\mathcal {C}}}$${\displaystyle {\mathcal {C}}}$2/3= 0,1222... ₃ = 0,1 2 ₃ = 0,2 0 ₃ und8/9= 0,21222... ₃ = 0,21 2 ₃ = 0,22 0 ₃ . Alle diese Endpunkte sind echte ternäre Brüche (Elemente von ) der Form${\displaystyle \mathbb{Z}\cdot 3^{-\mathbb{N}_{0}}}$P/Q, wobei Nenner q eine Potenz von 3 ist, wenn der Bruch in seiner irreduziblen Form vorliegt. Die ternäre Darstellung dieser Brüche endet (dh ist endlich) oder – erinnern Sie sich von oben, dass echte ternäre Brüche jeweils 2 Darstellungen haben – ist unendlich und „endet“ entweder in unendlich vielen wiederkehrenden Nullen oder unendlich vielen wiederkehrenden 2en. Eine solche Fraktion ist eine linke Grenzpunkt der , wenn seine ternäre Darstellung enthält keine 1en und „Enden“ in unendlich viele wiederkehrende 0s. In ähnlicher Weise ist ein echter ternärer Bruch ein rechter Grenzpunkt, wenn seine ternäre Entwicklung wiederum keine Einsen enthält und in unendlich vielen wiederkehrenden Zweien „endet“. ${\displaystyle {\mathcal {C}}}$${\displaystyle {\mathcal {C}}}$

Diese Menge von Endpunkten ist dicht in (aber nicht dicht in [0, 1]) und bildet eine abzählbar unendliche Menge. Die Zahlen, bei denen keine Endpunkte sind, haben in ihrer ternären Darstellung auch nur 0en und 2er, aber sie können nicht mit einer unendlichen Wiederholung der Ziffer 0 enden, auch nicht der Ziffer 2, weil es dann ein Endpunkt wäre. ${\displaystyle {\mathcal {C}}}$${\displaystyle {\mathcal {C}}}$

Die Funktion von bis [0,1] wird definiert, indem man die ternären Ziffern, die vollständig aus 0 und 2 bestehen, nimmt, alle 2 durch 1 ersetzt und die Folge als binäre Darstellung einer reellen Zahl interpretiert . In einer Formel, ${\displaystyle {\mathcal {C}}}$

${\displaystyle f{\bigg(}\sum_{k\in\mathbb{N}}a_{k}3^{-k}{\bigg)}=\sum_{k\in\mathbb{N} }{\frac {a_{k}}{2}}2^{-k}}$   wo   ${\displaystyle \forall k\in\mathbb{N} :a_{k}\in\{0,2\}.}$

Für jede Zahl y in [0,1] kann ihre binäre Darstellung in eine ternäre Darstellung einer Zahl x in übersetzt werden, indem alle Einsen durch Zweien ersetzt werden. Damit ist f ( x ) = y, so dass y im Bereich von f liegt . Zum Beispiel, wenn y =${\displaystyle {\mathcal {C}}}$3/5= 0.100110011001... ₂ = 0. 1001 , wir schreiben x = 0. 2002 = 0.200220022002... ₃ =7/10. Folglich ist f surjektiv. Allerdings f ist nicht injektiv - die Werte , für die f ( x ) zusammenfällt die an gegenüberliegenden Enden eines der ARE mittleren Drittel entfernt. Nimm zum Beispiel

1/3= 0.0 2 ₃ (das ist ein rechter Grenzpunkt und ein linker Grenzpunkt des mittleren Drittels [${\displaystyle {\mathcal {C}}}$1/3, 2/3]) und

2/3= 0,2 0 ₃ (das ist ein linker Grenzpunkt und ein rechter Grenzpunkt des mittleren Drittels [${\displaystyle {\mathcal {C}}}$1/3, 2/3])

so

${\displaystyle {\begin{array}{lcl}f{\bigl (}{}^{1}\!\!/\!_{3}{\bigr)}=f(0.0{\overline {2} }_{3})=0.0{\overline {1}}_{2}=\!\!&\!\!0.1_{2}\!\!&\!\!=0.1{\overline {0 }}_{2}=f(0,2{\overline {0}}_{3})=f{\bigl (}{}^{2}\!\!/\!_{3}{\bigr) }.\\&\parallel \\&{}^{1}\!\!/\!_{2}\end{array}}}$

Somit gibt es in der Cantor-Menge so viele Punkte wie im Intervall [0, 1] (das die überzählige Kardinalität hat ). Die Menge der Endpunkte der entfernten Intervalle ist jedoch zählbar, daher muss es in der Cantor-Menge unzählbar viele Zahlen geben, die keine Intervallendpunkte sind. Wie oben erwähnt, ist ein Beispiel für eine solche Zahl${\displaystyle {\mathfrak{c}}=2^{\aleph_{0}}}$1/4, Die als 0.020202 ... geschrieben werden können ₃ = 0. 02 in Ternärnotation. Tatsächlich gibt es solche, die gegeben sind . Dies wurde erstmals 1917 von Steinhaus nachgewiesen, der durch ein geometrisches Argument die äquivalente Behauptung bewies, dass für jede . Da diese Konstruktion eine Injektion von bis ermöglicht , haben wir als unmittelbare Folgerung. Unter der Annahme, dass für jede unendliche Menge (eine Aussage, die dem Auswahlaxiom von Tarski entspricht ) eine weitere Demonstration liefert, dass . ${\displaystyle a\in [-1,1]}$${\displaystyle x,y\in {\mathcal {C}}}$${\displaystyle a=yx}$${\displaystyle \{(x,y)\in\mathbb{R}^{2}\mid y=x+a\}\;\cap \;({\mathcal {C}}\times {\mathcal{ C}})\neq \emptyset}$${\displaystyle a\in [-1,1]}$${\displaystyle [-1,1]}$${\displaystyle {\mathcal {C}}\times {\mathcal {C}}}$${\displaystyle |{\mathcal {C}}\times {\mathcal {C}}|\geq |[-1,1]|={\mathfrak {c}}}$${\displaystyle |A\times A|=|A|}$${\displaystyle A}$${\displaystyle |{\mathcal{C}}|={\mathfrak{c}}}$

Die Cantor-Menge enthält so viele Punkte wie das Intervall, aus dem sie entnommen wurde, enthält jedoch selbst kein Intervall mit einer Länge ungleich Null. Die irrationalen Zahlen haben die gleiche Eigenschaft, aber die Cantor-Menge hat die zusätzliche Eigenschaft, abgeschlossen zu sein, also ist sie in keinem Intervall dicht, im Gegensatz zu den irrationalen Zahlen, die in jedem Intervall dicht sind.

Es wurde vermutet, dass alle algebraischen irrationalen Zahlen normal sind . Da Mitglieder der Cantor-Menge nicht normal sind, würde dies bedeuten, dass alle Mitglieder der Cantor-Menge entweder rational oder transzendental sind .

Selbstähnlichkeit

Die Cantor-Menge ist der Prototyp eines Fraktales . Es ist selbstähnlich , weil es gleich zwei Kopien von sich selbst ist, wenn jede Kopie um den Faktor 3 verkleinert und übersetzt wird. Genauer gesagt ist die Cantor-Menge gleich der Vereinigung zweier Funktionen, der linken und rechten Selbstähnlichkeitstransformationen von sich selbst und , die die Cantor-Menge bis zum Homöomorphismus invariant lassen :${\displaystyle T_{L}(x)=x/3}$${\displaystyle T_{R}(x)=(2+x)/3}$${\displaystyle T_{L}({\mathcal{C}})\cong T_{R}({\mathcal{C}})\cong {\mathcal{C}}=T_{L}({\mathcal{ C}})\cup T_{R}({\mathcal{C}}).}$

Wiederholte Iteration von und kann als unendlicher Binärbaum visualisiert werden . Das heißt, an jedem Knoten des Baums kann man den Unterbaum links oder rechts betrachten. Das Set zusammen mit der Funktionskomposition bildet ein Monoid , das dyadische Monoid . ${\displaystyle T_{L}}$${\displaystyle T_{R}}$${\displaystyle \{T_{L},T_{R}\}}$

Die Automorphismen des Binärbaums sind seine hyperbolischen Drehungen und werden durch die modulare Gruppe gegeben . Somit ist die Cantor-Menge ein homogener Raum in dem Sinne, dass für zwei beliebige Punkte und in der Cantor-Menge ein Homöomorphismus mit existiert . Eine explizite Konstruktion von lässt sich leichter beschreiben, wenn wir die Cantor-Menge als Produktraum von abzählbar vielen Kopien des diskreten Raums betrachten . Dann ist die durch definierte Abbildung ein involutiver Homöomorphismus, der und vertauscht . ${\displaystyle x}$${\displaystyle y}$${\displaystyle {\mathcal {C}}}$${\displaystyle h:{\mathcal{C}}\to {\mathcal{C}}}$${\displaystyle h(x)=y}$${\displaystyle h}$${\displaystyle \{0,1\}}$${\displaystyle h:\{0,1\}^{\mathbb{N}}\to \{0,1\}^{\mathbb{N}}}$${\displaystyle h_{n}(u):=u_{n}+x_{n}+y_{n}\mod 2}$${\displaystyle x}$${\displaystyle y}$

Naturschutzrecht

Es hat sich herausgestellt, dass für Skalierung und Selbstähnlichkeit immer irgendeine Form von Erhaltungsgesetz verantwortlich ist. Im Fall der Cantor-Menge ist zu sehen, dass das th-Moment (wo die fraktale Dimension ist) aller überlebenden Intervalle in jeder Phase des Konstruktionsprozesses gleich konstant ist, was im Fall der Cantor-Menge gleich eins ist. Wir wissen , dass es Intervalle der Größe in dem System im ten Schritt seiner Konstruktion. Wenn wir dann die überlebenden Intervalle als bezeichnen, dann ist der te Moment seit . ${\displaystyle d_{f}}$${\displaystyle d_{f}=\ln(2)/\ln(3)}$${\displaystyle N=2^{n}}$${\displaystyle 1/3^{n}}$${\displaystyle n}$${\displaystyle x_{1},x_{2},\ldots,x_{2^{n}}}$${\displaystyle d_{f}}$${\displaystyle x_{1}^{d_{f}}+x_{2}^{d_{f}}+\cdots +x_{2^{n}}^{d_{f}}=1}$${\displaystyle x_{1}=x_{2}=\cdots =x_{2^{n}}=1/3^{n}}$

Die Hausdorff-Dimension der Cantor-Menge ist gleich ln(2)/ln(3) 0,631.

Topologische und analytische Eigenschaften

Obwohl sich "die" Cantor-Menge typischerweise auf den oben beschriebenen ursprünglichen Cantor im mittleren Drittel bezieht, sprechen Topologen oft von "einer" Cantor-Menge, was jeden topologischen Raum bedeutet, der homöomorph (topologisch äquivalent) dazu ist.

Wie das obigen Summation Argument zeigt, ist die Cantor - Menge unzählbarer ist , aber Lebesguemaß 0. Da die Cantor - Menge das Komplement einer ist Vereinigung von offenen Mengen , sie selbst ist ein geschlossene Teilmenge der reellen Zahlen, und somit ein kompletter metrischer Raum . Da es auch total beschränkt ist , sagt der Satz von Heine-Borel , dass es kompakt sein muss .

Für jeden Punkt in der Cantor-Menge und jede beliebige kleine Umgebung des Punktes gibt es eine andere Zahl mit einer ternären Zahl von nur 0en und 2en sowie Zahlen, deren ternäre Zahlen eine 1 enthalten. Daher ist jeder Punkt in der Cantor-Menge ein Häufungspunkt (auch Clusterpunkt oder Grenzpunkt genannt) der Cantor-Menge, aber keiner ist ein innerer Punkt . Eine abgeschlossene Menge, in der jeder Punkt ein Häufungspunkt ist , wird in der Topologie auch als perfekte Menge bezeichnet , während eine abgeschlossene Teilmenge des Intervalls ohne innere Punkte im Intervall nirgendwo dicht ist .

Jeder Punkt der Cantor-Menge ist auch ein Häufungspunkt des Komplements der Cantor-Menge.

Für zwei beliebige Punkte in der Cantor-Menge gibt es eine ternäre Ziffer, bei der sie sich unterscheiden – einer hat 0 und der andere 2. Durch Aufteilen der Cantor-Menge in "Hälften" abhängig vom Wert dieser Ziffer erhält man eine Partition von die Cantor-Menge in zwei geschlossene Mengen, die die ursprünglichen zwei Punkte trennen. In der relativen Topologie auf der Cantor-Menge wurden die Punkte durch eine Clopen-Menge getrennt . Folglich ist die Cantor-Menge völlig getrennt . Als kompakter, völlig unverbundener Hausdorff-Raum ist die Cantor-Menge ein Beispiel für einen Steinraum .

Als topologischer Raum ist die Cantor - Menge natürlich homeomorphic auf das Produkt von abzählbar vielen Kopien des Raumes , in dem jede Kopie die trägt diskrete Topologie . Dies ist der Raum aller Folgen in zwei Ziffern ${\displaystyle \{0,1\}}$

${\displaystyle 2^{\mathbb{N}}=\{(x_{n})\mid x_{n}\in\{0,1\}{\text{ für }}n\in\mathbb{N } \},}$

die auch mit der Menge der 2-adischen ganzen Zahlen identifiziert werden kann . Die Grundlage für die offenen Sätze der Produkttopologie sind Zylindersätze ; der Homöomorphismus bildet diese auf die Unterraumtopologie ab , die die Cantor-Menge von der natürlichen Topologie auf der reellen Zahlengeraden erbt. Diese Charakterisierung des Cantor-Raums als Produkt kompakter Räume liefert einen zweiten Beweis dafür, dass der Cantor-Raum kompakt ist, über den Satz von Tychonoff .

Aus der obigen Charakterisierung ist die Cantor-Menge homöomorph zu den p-adischen ganzen Zahlen und, wenn ein Punkt davon entfernt wird, zu den p-adischen Zahlen .

Die Cantor-Menge ist eine Teilmenge der reellen Zahlen, die bezüglich der gewöhnlichen Distanzmetrik ein metrischer Raum sind ; daher ist die Cantor-Menge selbst ein metrischer Raum, indem dieselbe Metrik verwendet wird. Alternativ kann man die p-adische Metrik verwenden bei : gegebenen zwei Sequenzen ist der Abstand zwischen ihnen , wobei der kleinste Index so ist, dass ; gibt es keinen solchen Index, dann sind die beiden Folgen gleich, und man definiert den Abstand als Null. Diese beiden Metriken generieren dieselbe Topologie auf der Cantor-Menge. ${\displaystyle 2^{\mathbb{N}}}$${\displaystyle(x_{n}),(y_{n})\in 2^{\mathbb{N}}}$${\displaystyle d((x_{n}),(y_{n}))=2^{-k}}$${\displaystyle k}$${\displaystyle x_{k}\neq y_{k}}$

Wir haben oben gesehen, dass die Cantor-Menge ein völlig getrennter perfekter kompakter metrischer Raum ist. Tatsächlich ist er in gewisser Weise der einzige: Jeder nichtleere, total unzusammenhängende perfekte kompakte metrische Raum ist homöomorph zur Cantor-Menge. Siehe Cantor-Raum für mehr über Räume, die zur Cantor-Menge homöomorph sind.

Die Cantor-Menge wird manchmal als "universal" in der Kategorie der kompakten metrischen Räume angesehen , da jeder kompakte metrische Raum ein kontinuierliches Bild der Cantor-Menge ist; diese Konstruktion ist jedoch nicht einzigartig und daher ist die Cantor-Menge nicht im genauen kategorialen Sinne universell . Die "universelle" Eigenschaft hat wichtige Anwendungen in der Funktionalanalyse , wo sie manchmal als Darstellungssatz für kompakte metrische Räume bekannt ist .

Für jede ganze Zahl q ≥ 2 ist die Topologie auf der Gruppe G= Z _q ^ω (die abzählbare direkte Summe) diskret. Obwohl das Pontrjagin-Dual Γ auch Z _q ^{ω ist} , ist die Topologie von Γ kompakt. Man sieht, dass Γ total unzusammenhängend und perfekt ist – also homöomorph zur Cantor-Menge. Im Fall q = 2 ist es am einfachsten, den Homöomorphismus explizit auszuschreiben . (Siehe Rudin 1962, S. 40.)

Das geometrische Mittel der Cantor-Menge beträgt ungefähr 0,274974.

Maß und Wahrscheinlichkeit

Die Cantor-Menge kann als kompakte Gruppe binärer Folgen angesehen werden und ist als solche mit einem natürlichen Haar-Maß ausgestattet . Wenn es so normalisiert wird, dass das Maß des Satzes 1 ist, ist es ein Modell einer unendlichen Folge von Münzwürfen. Außerdem kann man zeigen, dass das übliche Lebesgue-Maß auf dem Intervall ein Abbild des Haar-Maßes auf der Cantor-Menge ist, während die natürliche Injektion in die ternäre Menge ein kanonisches Beispiel für ein singuläres Maß ist . Es kann auch gezeigt werden, dass das Haar-Maß ein Bild einer beliebigen Wahrscheinlichkeit ist , was den Cantor-Satz in gewisser Weise zu einem universellen Wahrscheinlichkeitsraum macht.

In der Lebesgue- Maßtheorie ist die Cantor-Menge ein Beispiel für eine Menge, die nicht abzählbar ist und kein Maß hat.

Kantorenzahlen

Wenn wir eine Cantor-Zahl als Mitglied der Cantor-Menge definieren, dann

1. Jede reelle Zahl in [0, 2] ist die Summe zweier Cantor-Zahlen.
2. Zwischen zwei beliebigen Cantor-Zahlen steht eine Zahl, die keine Cantor-Zahl ist.

Beschreibende Mengenlehre

Die Cantor-Menge ist eine magere Menge (oder eine Menge der ersten Kategorie) als Teilmenge von [0,1] (jedoch nicht als Teilmenge ihrer selbst, da sie ein Baire-Raum ist ). Die Cantor-Menge demonstriert somit, dass Begriffe von "Größe" in Bezug auf Kardinalität, Maß und (Baire-)Kategorie nicht übereinstimmen müssen. Wie die Menge ist die Cantor-Menge "klein" in dem Sinne, dass sie eine Nullmenge (eine Menge von Maß Null) und eine magere Teilmenge von [0,1] ist. Im Gegensatz zu , das abzählbar ist und eine "kleine" Kardinalität hat, ist die Kardinalität von jedoch die gleiche wie die von [0,1], dem Kontinuum , und ist "groß" im Sinne der Kardinalität. In der Tat ist es auch möglich , eine Teilmenge von [0,1] zu konstruieren , die mageren aber positiver Maßnahme ist und eine Teilmenge , die nicht mager ist , aber vom Maße Null: Durch die abzählbare Vereinigung von „Fett“ Cantor setzt unter der Maßnahme (zur Konstruktion siehe Smith–Volterra–Cantor-Menge weiter unten), erhalten wir eine Menge, die ein positives Maß (gleich 1) hat, aber in [0,1] mager ist, da jede nirgends dicht ist. Betrachten Sie dann die Menge . Da , nicht mager sein, aber da , muss Maß Null. ${\displaystyle \mathbb{Q} \cap [0,1]}$${\displaystyle {\mathcal {C}}}$${\displaystyle \mathbb{Q} \cap [0,1]}$${\displaystyle \aleph _{0}}$${\displaystyle {\mathcal {C}}}$${\displaystyle {\mathfrak{c}}}$${\displaystyle {\mathcal {C}}^{(n)}}$${\displaystyle \lambda =(n-1)/n}$${\textstyle {\mathcal{A}}:=\bigcup_{n=1}^{\infty }{\mathcal{C}}^{(n)}}$${\displaystyle {\mathcal {C}}^{(n)}}$${\textstyle {\mathcal{A}}^{\mathrm{c}}=[0,1]\setminus \bigcup_{n=1}^{\infty }{\mathcal{C}}^{(n )}}$${\displaystyle {\mathcal{A}}\cup {\mathcal{A}}^{\mathrm {c}}=[0,1]}$${\displaystyle {\mathcal{A}}^{\mathrm{c}}}$${\displaystyle \mu({\mathcal{A}})=1}$${\displaystyle {\mathcal{A}}^{\mathrm{c}}}$

Varianten

Smith–Volterra–Cantor-Set

Anstatt wie im Cantor-Set das mittlere Drittel jedes Stücks wiederholt zu entfernen, könnten wir auch jeden anderen festen Prozentsatz (außer 0% und 100%) aus der Mitte entfernen. In dem Fall, in dem die Mitte8/10des Intervalls entfernt wird, erhalten wir einen bemerkenswert zugänglichen Fall – die Menge besteht aus allen Zahlen in [0,1], die als Dezimalzahl geschrieben werden können, die ausschließlich aus 0 und 9 besteht. Wenn ein fester Prozentsatz in jeder Stufe entfernt wird, dann wird der Begrenzungssatz hat Maß Null, da die Länge des Rests , wie für jeden f derart , daß . ${\displaystyle (1-f)^{n}\to 0}$${\displaystyle n\to\infty}$${\displaystyle 0<f\leq 1}$

Andererseits können "fette Cantor-Sätze" mit positivem Maß erzeugt werden, indem in jeder Iteration kleinere Bruchteile der Mitte des Segments entfernt werden. Somit kann man zur Cantor-Menge homöomorphe Mengen konstruieren, die ein positives Lebesgue-Maß haben, aber dennoch nirgendwo dicht sind. Wenn bei der n- ten Iteration ein Längenintervall ( ) aus der Mitte jedes Segments entfernt wird , dann ist die entfernte Gesamtlänge , und die begrenzende Menge hat ein Lebesgue-Maß von . Somit ist die Cantor-Menge im mittleren Drittel gewissermaßen ein Grenzfall mit . Wenn , dann hat der Rest ein positives Maß mit . Der Fall ist als Smith-Volterra-Cantor-Satz bekannt , der ein Lebesgue-Maß von hat . ${\displaystyle r^{n}}$${\displaystyle r\leq 1/3}$${\textstyle \sum _{n=1}^{\infty}2^{n-1}r^{n}=r/(1-2r)}$${\displaystyle \lambda =(1-3r)/(1-2r)}$${\displaystyle r=1/3}$${\displaystyle 0<r<1/3}$${\displaystyle 0<\lambda<1}$${\displaystyle r=1/4}$${\displaystyle 1/2}$

Stochastisches Cantor-Set

Man kann die Konstruktion der Cantor-Menge modifizieren, indem man zufällig statt gleichmäßig teilt. Außerdem können wir, um die Zeit einzubeziehen, bei jedem Schritt nur eines der verfügbaren Intervalle teilen, anstatt alle verfügbaren Intervalle zu teilen. Im Fall einer stochastischen triadischen Cantor-Menge kann der resultierende Prozess durch die folgende Geschwindigkeitsgleichung beschrieben werden

${\displaystyle {\frac {\partial c(x,t)}{\partial t}}=-{\frac {x^{2}}{2}}c(x,t)+2\int _{ x}^{\infty}(yx)c(y,t)\,dy,}$

und für die stochastische dyadische Cantor-Menge

${\displaystyle {{\partial c(x,t)} \over {\partial t}}=-xc(x,t)+(1+p)\int _{x}^{\infty}c(y ,t)\,dy,}$

wobei die Anzahl der Größenintervalle zwischen und ist . Im Fall von triadischen Cantor-Mengen ist die fraktale Dimension kleiner als ihr deterministisches Gegenstück . Im Fall der stochastischen dyadischen Cantor-Menge ist die fraktale Dimension wiederum kleiner als die ihres deterministischen Gegenstücks . Im Fall der stochastischen dyadischen Cantor-Menge weist die Lösung für dynamische Skalierung auf, da ihre Lösung im Langzeitlimit dort liegt, wo die fraktale Dimension der stochastischen dyadischen Cantor-Menge liegt . In beiden Fällen sind auch das te Moment ( ) der stochastischen triadischen und der dyadischen Cantor-Menge Erhaltungsgrößen. ${\displaystyle c(x,t)dx}$${\displaystyle x}$${\displaystyle x+dx}$${\displaystyle 0.5616}$${\displaystyle 0.6309}$${\displaystyle p}$${\displaystyle \ln(1+p)/\ln2}$${\displaystyle c(x,t)}$${\displaystyle t^{-(1+d_{f})}e^{-xt}}$${\displaystyle d_{f}=p}$${\displaystyle d_{f}}$${\textstyle \int x^{d_{f}}c(x,t)\,dx={\text{konstante}}}$

Kantorenstaub

Cantor Dust ist eine mehrdimensionale Version des Cantor-Sets. Er kann gebildet werden, indem man ein endliches kartesisches Produkt der Cantor-Menge mit sich selbst nimmt, was ihn zu einem Cantor-Raum macht . Wie das Cantor-Set hat Cantor-Staub null Maß .

Cantor-Würfel Rekursionsfortschritt in Richtung Cantor-Staub

Kantorenstaub (2D)

Kantorenstaub (3D)

Ein anderes 2D-Analogon des Cantor-Sets ist der Sierpinski-Teppich , bei dem ein Quadrat in neun kleinere Quadrate unterteilt und das mittlere entfernt wird. Die verbleibenden Quadrate werden dann weiter in jeweils neun unterteilt und die Mitte entfernt, und so weiter bis ins Unendliche. Ein 3D-Analogon davon ist der Menger-Schwamm .

Historische Bemerkungen

Spaltenkapital mit Muster, das an die Cantor-Menge erinnert, aber nicht ternär, sondern binär ausgedrückt. Kupferstich der Île de Philae aus der Beschreibung d'Égypte von Jean-Baptiste Prosper Jollois und Édouard Devilliers, Imprimerie Impériale, Paris, 1809-1828

Cantor selbst definierte die Menge in allgemeiner, abstrakter Weise und erwähnte die ternäre Konstruktion nur am Rande, als Beispiel für eine allgemeinere Idee, die einer perfekten Menge , die nirgendwo dicht ist . Das Originalpapier bietet mehrere verschiedene Konstruktionen des abstrakten Konzepts.

Dieses Set wäre zu der Zeit, als Cantor es erdachte, als abstrakt angesehen worden. Cantor selbst wurde dazu geführt durch praktische Bedenken hinsichtlich der Menge von Punkten, an denen eine trigonometrische Reihe möglicherweise nicht konvergiert. Die Entdeckung trug viel dazu bei, ihn auf den Weg zu bringen, eine abstrakte, allgemeine Theorie der unendlichen Mengen zu entwickeln .

Siehe auch

• Die Indikatorfunktion des Cantor-Sets
• Smith–Volterra–Cantor-Set
• Hexagramme (I Ging)
• Cantor-Funktion
• Kantorwürfel
• Antoines Halskette
• Koch-Schneeflocke
• Knaster-Kuratowski-Fan
• Liste der Fraktale nach Hausdorff-Dimension
• Moser–de Bruijn-Folge

Anmerkungen

Verweise

Externe Links

• "Kantorensatz" , Enzyklopädie der Mathematik , EMS Press , 2001 [1994]
• Cantor Sets und Cantor Set und Funktion auf den Punkt
• Cantor Set in Platonischen Reichen