Mikromagnetik - Micromagnetics

Die Mikromagnetik ist ein Gebiet der Physik, das sich mit der Vorhersage magnetischer Verhaltensweisen auf Längenskalen im Submikrometerbereich befasst. Die betrachteten Längenskalen sind groß genug, um die Atomstruktur des Materials zu ignorieren ( Kontinuumsnäherung ), aber klein genug, um magnetische Strukturen wie Domänenwände oder Wirbel aufzulösen .

Die Mikromagnetik kann mit statischen Gleichgewichten umgehen , indem sie die magnetische Energie minimiert, und mit dynamischem Verhalten, indem sie die zeitabhängige dynamische Gleichung löst.

Geschichte

Die Mikromagnetik als Feld ( dh das sich speziell mit dem Verhalten ferromagnetischer Materialien auf Längenskalen im Submikrometerbereich befasst) wurde 1963 eingeführt, als William Fuller Brown Jr. einen Artikel über antiparallele Domänenwandstrukturen veröffentlichte. Bis vor relativ kurzer Zeit war die rechnergestützte Mikromagnetik in Bezug auf die Rechenleistung unerschwinglich teuer, aber kleinere Probleme sind jetzt auf einem modernen Desktop- PC lösbar .

Statische Mikromagnetik

Der Zweck der statischen Mikromagnetik besteht darin, die räumliche Verteilung der Magnetisierung M im Gleichgewicht zu ermitteln. In den meisten Fällen ist der Modul | , da die Temperatur viel niedriger als die Curie-Temperatur des betrachteten Materials ist M | der Magnetisierung wird angenommen, dass sie überall gleich der Sättigungsmagnetisierung M _{s ist} . Das Problem besteht dann darin, die räumliche Orientierung der Magnetisierung zu finden, die durch den Magnetisierungsrichtungsvektor m = M / M _{s gegeben ist} , der auch als reduzierte Magnetisierung bezeichnet wird .

Die statischen Gleichgewichte werden durch Minimierung der magnetischen Energie gefunden,

${\ displaystyle E = E _ {\ text {exchange}} + E _ {\ text {anis}} + E _ {\ text {Z}} + E _ {\ text {demag}} + E _ {\ text {me}}}$ ,

vorbehaltlich der Einschränkung | M | = M _s oder | m | = 1.

Die Beiträge zu dieser Energie sind folgende:

Energie austauschen

Die Austauschenergie ist eine phänomenologische Kontinuumsbeschreibung der quantenmechanischen Austauschwechselwirkung . Es ist geschrieben als:

${\ displaystyle E _ {\ text {exchange}} = A \ int _ {V} \ left ((\ nabla m_ {x}) ^ {2} + (\ nabla m_ {y}) ^ {2} + (\ nabla m_ {z}) ^ {2} \ right) \ mathrm {d} V}$

wobei A die Austauschkonstante ist ; m _x , m _y und m _z sind die Komponenten von m ; und das Integral wird über das Volumen der Probe durchgeführt.

Die Austauschenergie begünstigt tendenziell Konfigurationen, bei denen die Magnetisierung über die Probe nur langsam variiert. Diese Energie wird minimiert, wenn die Magnetisierung vollkommen gleichmäßig ist.

Anisotropieenergie

Die magnetische Anisotropie entsteht aufgrund einer Kombination aus Kristallstruktur und Spin-Bahn-Wechselwirkung . Es kann allgemein geschrieben werden als:

${\ displaystyle E _ {\ text {anis}} = \ int _ {V} F _ {\ text {anis}} (\ mathbf {m}) \ mathrm {d} V}$

wobei F _anis , die Anisotropieenergiedichte, eine Funktion der Ausrichtung der Magnetisierung ist. Richtungen mit minimaler Energie für F _anis werden einfache Achsen genannt .

Die Zeitumkehrsymmetrie stellt sicher, dass F _anis eine gerade Funktion von m ist . Die einfachste solche Funktion ist

${\ displaystyle F _ {\ text {anis}} (\ mathbf {m}) = - Km_ {z} ^ {2}}$ .

wobei K die Anisotropiekonstante genannt wird . In dieser als uniaxiale Anisotropie bezeichneten Näherung ist die einfache Achse die z- Richtung.

Die Anisotropieenergie begünstigt magnetische Konfigurationen, bei denen die Magnetisierung überall entlang einer einfachen Achse ausgerichtet ist.

Zeeman Energie

Die Zeeman-Energie ist die Wechselwirkungsenergie zwischen der Magnetisierung und einem von außen angelegten Feld. Es ist geschrieben als:

${\ displaystyle E _ {\ text {Z}} = - \ mu _ {0} \ int _ {V} \ mathbf {M} \ cdot \ mathbf {H} _ {\ text {a}} \ mathrm {d} V}$

Dabei ist H _a das angelegte Feld und µ ₀ die Vakuumpermeabilität .

Die Zeeman-Energie begünstigt die Ausrichtung der Magnetisierung parallel zum angelegten Feld.

Energie des Entmagnetisierungsfeldes

Beispiel einer mikromagnetischen Konfiguration. Im Vergleich zu einem gleichmäßigen Zustand senkt die Flussschlussstruktur die Energie des Entmagnetisierungsfeldes auf Kosten einer gewissen Austauschenergie.

Das Entmagnetisierungsfeld ist das Magnetfeld, das von der Magnetprobe auf sich selbst erzeugt wird. Die damit verbundene Energie ist:

${\ displaystyle E _ {\ text {demag}} = - {\ frac {\ mu _ {0}} {2}} \ int _ {V} \ mathbf {M} \ cdot \ mathbf {H} _ {\ text {d}} \ mathrm {d} V}$

wobei H _d das Entmagnetisierungsfeld ist . Dieses Feld hängt von der magnetischen Konfiguration selbst ab und kann durch Lösen von:

${\ displaystyle \ nabla \ cdot \ mathbf {H} _ {\ text {d}} = - \ nabla \ cdot \ mathbf {M}}$

${\ displaystyle \ nabla \ times \ mathbf {H} _ {\ text {d}} = 0}$

wobei −∇ · M manchmal als magnetische Ladungsdichte bezeichnet wird . Die Lösung dieser Gleichungen (vgl. Magnetostatik ) lautet:

${\ displaystyle \ mathbf {H} _ {\ text {d}} = - {\ frac {1} {4 \ pi}} \ int _ {V} \ nabla \ cdot \ mathbf {M} {\ frac {\ mathbf {r}} {r ^ {3}}} \ mathrm {d} V}$

Dabei ist r der Vektor, der vom aktuellen Integrationspunkt zu dem Punkt geht, an dem H _d berechnet wird.

Es ist anzumerken, dass die magnetische Ladungsdichte an den Rändern der Probe unendlich sein kann, da sich M diskontinuierlich von einem endlichen Wert innerhalb innerhalb von Null außerhalb der Probe ändert. Dies wird normalerweise durch die Verwendung geeigneter Randbedingungen am Rand der Probe behoben.

Die Energie des Entmagnetisierungsfeldes begünstigt magnetische Konfigurationen, die magnetische Ladungen minimieren. Insbesondere an den Rändern der Probe neigt die Magnetisierung dazu, parallel zur Oberfläche zu verlaufen. In den meisten Fällen ist es nicht möglich, diesen Energieterm gleichzeitig mit den anderen zu minimieren. Das statische Gleichgewicht ist dann ein Kompromiss, der die gesamte magnetische Energie minimiert, obwohl es möglicherweise keinen bestimmten Begriff einzeln minimiert.

Magnetoelastische Energie

Die magnetoelastische Energie beschreibt den Energiespeicher aufgrund elastischer Gitterverzerrungen. Es kann vernachlässigt werden, wenn magnetoelastisch gekoppelte Effekte vernachlässigt werden. Es gibt eine bevorzugte lokale Verzerrung des kristallinen Feststoffs, die mit dem Magnetisierungsdirektor m ,. Für ein einfaches Modell kann man annehmen, dass diese Dehnung in lateraler Richtung isochor und vollständig isotrop ist, was den deviatorischen Ansatz ergibt

${\ displaystyle \ mathbf {\ varepsilon} _ {0} (\ mathbf {m}) = {\ frac {3} {2}} E \, [\ mathbf {m} \ otimes \ mathbf {m} - {\ frac {1} {3}} \ mathbf {1}]}$

wobei der Materialparameter E> 0 die magnetostriktive Konstante ist. Es ist klar, dass E die durch die Magnetisierung in Richtung m induzierte Dehnung ist . Mit diesem Ansatz betrachten wir die elastische Energiedichte als eine Funktion der elastischen, spannungserzeugenden Dehnungen . Eine quadratische Form für die magnetoelastische Energie ist ${\ displaystyle \ mathbf {\ varepsilon} _ {e}: = \ mathbf {\ varepsilon} - \ mathbf {\ varepsilon} _ {0}}$

${\ displaystyle E _ {\ text {me}} = {\ frac {1} {2}} [\ mathbf {\ varepsilon} - \ mathbf {\ varepsilon} _ {0} (\ mathbf {m})]: \ mathbb {C}: [\ mathbf {\ varepsilon} - \ mathbf {\ varepsilon} _ {0} (\ mathbf {m})]}$

wo ist der Elastizitätstensor vierter Ordnung. Hier wird angenommen, dass die elastische Antwort isotrop ist (basierend auf den beiden Lamé-Konstanten λ und μ). Unter Berücksichtigung der konstanten Länge von m erhalten wir die invariantenbasierte Darstellung ${\ displaystyle \ mathbb {C}: = \ lambda \ mathbf {1} \ otimes \ mathbf {1} +2 \ mu \ mathbb {I}}$

${\ displaystyle E _ {\ text {me}} = {\ frac {\ lambda} {2}} {\ mbox {tr}} ^ {2} [\ mathbf {\ varepsilon}] + \ mu \, {\ mbox {tr}} [\ mathbf {\ varepsilon} ^ {2}] - 3 \ mu E {\ big \ {} {\ mbox {tr}} [\ mathbf {\ varepsilon} (\ mathbf {m} \ otimes \ mathbf {m})] - {\ frac {1} {3}} {\ mbox {tr}} [\ mathbf {\ varepsilon}] {\ big \}}.}$

Dieser Energiebegriff trägt zur Magnetostriktion bei.

Dynamische Mikromagnetik

Der Zweck der dynamischen Mikromagnetik besteht darin, die zeitliche Entwicklung der magnetischen Konfiguration einer Probe unter bestimmten instationären Bedingungen wie dem Anlegen eines Feldimpulses oder eines Wechselstromfeldes vorherzusagen. Dies geschieht durch Lösen der Landau-Lifshitz-Gilbert-Gleichung , einer partiellen Differentialgleichung, die die Entwicklung der Magnetisierung anhand des auf sie einwirkenden lokalen effektiven Feldes beschreibt .

Effektives Feld

Das effektive Feld ist das lokale Feld , das durch die Magnetisierung gefühlt wird. Es kann informell als Ableitung der magnetischen Energiedichte in Bezug auf die Ausrichtung der Magnetisierung beschrieben werden, wie in:

${\ displaystyle \ mathbf {H} _ {\ mathrm {eff}} = - {\ frac {1} {\ mu _ {0} M_ {s}}} {\ frac {\ mathrm {d} ^ {2} E} {\ mathrm {d} \ mathbf {m} \ mathrm {d} V}}}$

wobei d E / d V die Energiedichte ist. In Variationsbedingungen eine Änderung d m der Magnetisierung und die damit verbundenen Änderung d E sind der magnetischen Energie im Zusammenhang mit:

${\ displaystyle \ mathrm {d} E = - \ mu _ {0} M_ {s} \ int _ {V} (\ mathrm {d} \ mathbf {m}) \ cdot \ mathbf {H} _ {\ text {eff}} \, \ mathrm {d} V}$

Da m ein Einheitsvektor ist, steht d m immer senkrecht zu m . Dann lässt die obige Definition die Komponente von H _eff , die parallel zu m ist, nicht spezifiziert . Dies ist normalerweise kein Problem, da diese Komponente keinen Einfluss auf die Magnetisierungsdynamik hat.

Aus dem Ausdruck der verschiedenen Beiträge zur magnetischen Energie ergibt sich: Das effektive Feld ist:

${\ displaystyle \ mathbf {H} _ {\ mathrm {eff}} = {\ frac {2A} {\ mu _ {0} M_ {s}}} \ nabla ^ {2} \ mathbf {m} - {\ frac {1} {\ mu _ {0} M_ {s}}} {\ frac {\ partielles F _ {\ text {anis}}} {\ partielles \ mathbf {m}}} + \ mathbf {H} _ { \ text {a}} + \ mathbf {H} _ {\ text {d}}}$

Landau-Lifshitz-Gilbert-Gleichung

Die Terme der Landau-Lifshitz-Gilbert-Gleichung: Präzession (rot) und Dämpfung (blau). Die Trajektorie der Magnetisierung (gepunktete Spirale) wird unter der vereinfachenden Annahme gezeichnet, dass das effektive Feld H _eff konstant ist.

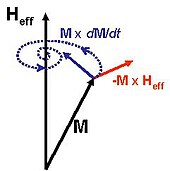
Dies ist die Bewegungsgleichung der Magnetisierung. Es beschreibt eine Larmor-Präzession der Magnetisierung um das effektive Feld, wobei sich ein zusätzlicher Dämpfungsterm aus der Kopplung des Magnetsystems an die Umgebung ergibt. Die Gleichung kann in der sogenannten Gilbert-Form (oder impliziten Form) wie folgt geschrieben werden :

${\ displaystyle {\ frac {\ partielle \ mathbf {m}} {\ partielle t}} = - | \ gamma | \ mathbf {m} \ times \ mathbf {H} _ {\ mathrm {eff}} + \ alpha \ mathbf {m} \ times {\ frac {\ teilweise \ mathbf {m}} {\ teilweise t}}}$

Dabei ist γ das elektronengyromagnetische Verhältnis und α die Gilbert-Dämpfungskonstante.

Es kann gezeigt werden, dass dies mathematisch der folgenden Landau-Lifshitz- Form (oder expliziten Form) entspricht:

${\ displaystyle {\ frac {\ partielle \ mathbf {m}} {\ partielle t}} = - {\ frac {| \ gamma |} {1+ \ alpha ^ {2}}} \ mathbf {m} \ times \ mathbf {H} _ {\ mathrm {eff}} - {\ frac {\ alpha | \ gamma |} {1+ \ alpha ^ {2}}} \ mathbf {m} \ times (\ mathbf {m} \ times \ mathbf {H} _ {\ text {eff}})}$

Anwendungen

Die Wechselwirkung von Mikromagnetik mit Mechanik ist auch im Zusammenhang mit industriellen Anwendungen von Interesse, die sich mit magnetoakustischer Resonanz befassen, wie z. B. in Hypersound-Lautsprechern, magnetostriktiven Hochfrequenzwandlern usw. FEM-Simulationen, die den Effekt der Magnetostriktion auf Mikromagnetik berücksichtigen, sind von Bedeutung. Solche Simulationen verwenden die oben beschriebenen Modelle innerhalb eines Finite-Elemente-Rahmens.

Neben herkömmlichen magnetischen Domänen und Domänenwänden behandelt die Theorie auch die Statik und Dynamik topologischer Linien- und Punktkonfigurationen, z. B. magnetische Wirbel- und Antivortexzustände; oder sogar 3d-Bloch-Punkte, an denen beispielsweise die Magnetisierung vom Ursprung radial in alle Richtungen oder in topologisch äquivalente Konfigurationen führt. So werden sowohl räumlich als auch zeitlich Nano- (und sogar Piko-) Skalen verwendet.

Es wird angenommen, dass die entsprechenden topologischen Quantenzahlen als Informationsträger verwendet werden, um die neuesten und bereits untersuchten Aussagen in der Informationstechnologie anzuwenden .

Eine weitere Anwendung, die sich im letzten Jahrzehnt herausgebildet hat, ist die Anwendung der Mikromagnetik zur neuronalen Stimulation. In dieser Disziplin werden numerische Methoden wie die Finite-Elemente-Analyse verwendet, um die vom Stimulationsapparat erzeugten elektrischen / magnetischen Felder zu analysieren; Anschließend werden die Ergebnisse mithilfe einer neuronalen In-vivo-Stimulation oder einer In-vitro-Stimulation validiert oder weiter untersucht. Unter Verwendung dieser Methodik wurden mehrere unterschiedliche Neuronengruppen untersucht, darunter Netzhautneuronen, Cochlea-Neuronen, vestibuläre Neuronen und kortikale Neuronen embryonaler Ratten.

Siehe auch

• Magnetismus
• Magnetische Nanopartikel

Fußnoten und Referenzen

Weiterführende Literatur

Externe Links

• µMAG - Aktivitätsgruppe für mikromagnetische Modellierung .
• OOMMF - Mikromagnetisches Modellierungswerkzeug .
• MuMax - GPU-beschleunigtes mikromagnetisches Modellierungswerkzeug .