Verma-Modul - Verma module

Verma-Module , benannt nach Daya-Nand Verma , sind Objekte in der Darstellungstheorie der Lie-Algebren , einem Zweig der Mathematik .

Verma-Module können bei der Klassifizierung irreduzibler Darstellungen einer komplexen halbeinfachen Lie-Algebra verwendet werden. Insbesondere obwohl ichduersiees Verma Module unendlichdimensionalen ist, Quotienten von ihnen können verwendet werden , endlich-dimensionale Darstellungen mit höchstem Gewicht zu konstruieren , wo ist dominant und Integral. Ihre Homomorphismen entsprechen invarianten Differentialoperatoren über Flag-Mannigfaltigkeiten . ${\displaystyle \lambda}$${\displaystyle \lambda}$

Informelles Bauen

Wir können die Idee eines Verma-Moduls wie folgt erklären. Sei eine halbeinfache Lie-Algebra (über , der Einfachheit halber). Sei eine feste Cartan-Subalgebra von und sei das zugehörige Wurzelsystem. Sei eine feste Menge positiver Nullstellen. Wählen Sie für jeden ein Element ungleich null für den entsprechenden Wurzelraum und ein Element ungleich null im Wurzelraum aus . Wir betrachten das 's als "Erhöhungsoperatoren" und das 's als "senkende Operatoren". ${\displaystyle {\mathfrak {g}}}$${\displaystyle \mathbb{C}}$${\displaystyle {\mathfrak{h}}}$${\displaystyle {\mathfrak {g}}}$${\displaystyle R}$${\displaystyle R^{+}}$${\displaystyle \alpha\in R^{+}}$${\displaystyle X_{\alpha}}$${\displaystyle {\mathfrak {g}}_{\alpha}}$${\displaystyle Y_{\alpha}}$${\displaystyle {\mathfrak {g}}_{-\alpha}}$${\displaystyle X_{\alpha}}$${\displaystyle Y_{\alpha}}$

Sei nun ein beliebiges lineares Funktional, nicht unbedingt dominant oder integral. Unser Ziel ist es, eine Darstellung von mit höchstem Gewicht zu konstruieren , die durch einen einzelnen von Null verschiedenen Vektor mit Gewicht erzeugt wird . Das Verma-Modul ist ein solches Modul mit dem höchsten Gewicht, das in dem Sinne maximal ist, dass jedes andere Modul mit dem höchsten Gewicht mit dem höchsten Gewicht ein Quotient des Verma-Moduls ist. Es wird sich herausstellen, dass Verma-Module immer unendlich dimensional sind; Wenn jedoch ein dominantes Integral ist, kann man einen endlichdimensionalen Quotientenmodul des Verma-Moduls konstruieren. Somit spielen Verma-Module eine wichtige Rolle bei der Klassifizierung endlich-dimensionaler Darstellungen von . Insbesondere sind sie ein wichtiges Werkzeug im harten Teil des Satzes vom höchsten Gewicht, nämlich zu zeigen, dass jedes dominante Integralelement tatsächlich als das höchste Gewicht einer endlichdimensionalen irreduziblen Darstellung von entsteht . ${\displaystyle \lambda\in {\mathfrak{h}}^{*}}$${\displaystyle W_{\lambda}}$${\displaystyle {\mathfrak {g}}}$${\displaystyle \lambda}$${\displaystyle v}$${\displaystyle \lambda}$${\displaystyle \lambda}$${\displaystyle \lambda}$${\displaystyle {\mathfrak {g}}}$${\displaystyle {\mathfrak {g}}}$

Wir versuchen nun intuitiv zu verstehen, wie das Verma-Modul mit dem höchsten Gewicht aussehen soll. Da soll ein Vektor mit höchstem Gewicht mit weight sein , wollen wir sicherlich ${\displaystyle \lambda}$${\displaystyle v}$${\displaystyle \lambda}$

${\displaystyle H\cdot v=\lambda(H)v,\quad H\in {\mathfrak{h}}}$

und

${\displaystyle X_{\alpha}\cdot v=0,\quad\alpha\in R^{+}}$.

Dann sollten überspannte Elemente durch Absenken durch die Aktion des 's erhalten werden: ${\displaystyle W_{\lambda}}$${\displaystyle v}$${\displaystyle Y_{\alpha}}$

${\displaystyle Y_{\alpha_{i_{1}}}\cdots Y_{\alpha_{i_{M}}}\cdot v}$.

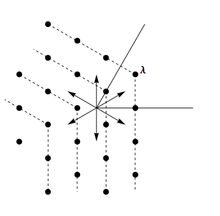
Wir erlegen jetzt nur die Beziehungen zwischen Vektoren der obigen Form auf, die für die Kommutierungsbeziehungen zwischen den 's erforderlich sind . Insbesondere das Verma-Modul ist immer unendlichdimensional. Die Gewichte des Verma-Moduls mit der höchsten Gewichtung bestehen aus allen Elementen , die durch Subtrahieren ganzzahliger Kombinationen positiver Wurzeln erhalten werden können. Die Abbildung zeigt die Gewichte eines Verma-Moduls für . ${\displaystyle Y}$${\displaystyle \lambda}$${\displaystyle\mu}$${\displaystyle \lambda}$${\displaystyle\mathrm{sl} (3;\mathbb{C})}$

Ein einfaches Umordnungsargument zeigt, dass es nur einen möglichen Weg gibt, wie die vollständige Lie-Algebra auf diesem Raum wirken kann. Insbesondere, wenn ein Element von ist , dann können wir mit dem einfachen Teil des Poincaré-Birkhoff-Witt-Theorems umschreiben ${\displaystyle {\mathfrak {g}}}$${\displaystyle Z}$${\displaystyle {\mathfrak {g}}}$

${\displaystyle ZY_{\alpha_{i_{1}}}\cdots Y_{\alpha_{i_{M}}}}$

als Linearkombination von Produkten von Lie-Algebra-Elementen, wobei zuerst die Erhöhungsoperatoren , die Elemente der Cartan-Subalgebra und zuletzt die Erniedrigungsoperatoren wirken . Wendet man diese Summe von Termen auf an , ist jeder Term mit einem Erhöhungsoperator null, alle Faktoren im Cartan wirken als Skalare, und somit erhalten wir ein Element der ursprünglichen Form. ${\displaystyle X_{\alpha}}$${\displaystyle Y_{\alpha}}$${\displaystyle v}$

Um die Struktur des Verma-Moduls etwas besser zu verstehen, können wir eine Ordnung der positiven Wurzeln als wählen und die entsprechenden Absenkungsoperatoren mit lassen . Dann kann durch ein einfaches Umordnungsargument jedes Element der obigen Form als Linearkombination von Elementen mit den 's in einer bestimmten Reihenfolge umgeschrieben werden: ${\displaystyle \alpha_{1},\ldots\alpha_{n}}$${\displaystyle Y_{1},\ldots Y_{n}}$${\displaystyle Y}$

${\displaystyle Y_{1}^{k_{1}}\cdots Y_{n}^{k_{n}}v}$,

wobei die 's nicht negative ganze Zahlen sind. Tatsächlich stellt sich heraus, dass solche Vektoren eine Grundlage für das Verma-Modul bilden. ${\displaystyle k_{j}}$

Obwohl diese Beschreibung des Verma-Moduls eine intuitive Vorstellung davon vermittelt, wie es aussieht, muss es dennoch rigoros konstruiert werden. Auf jeden Fall liefert das Verma-Modul – für alle , nicht unbedingt dominant oder ganzzahlig – eine Darstellung mit höchstem Gewicht . Der Preis, den wir für diese relativ einfache Konstruktion zahlen, ist, dass sie immer unendlich dimensional ist. Für den Fall, dass dominant und ganzzahlig ist, kann man einen endlichdimensionalen, irreduziblen Quotienten des Verma-Moduls konstruieren. ${\displaystyle W_{\lambda}}$ ${\displaystyle \lambda}$${\displaystyle \lambda}$${\displaystyle W_{\lambda}}$${\displaystyle \lambda}$

Der Fall von sl(2; C)

Seien Sie die übliche Grundlage für : ${\displaystyle {X,Y,H}}$${\displaystyle \mathrm{sl} (2;\mathbb{C})}$

${\displaystyle X={\begin{pmatrix}0&1\\0&0\end{pmatrix}}\qquad Y={\begin{pmatrix}0&0\\1&0\end{pmatrix}}\qquad H={\begin{pmatrix }1&0\\0&-1\end{pmatrix}}~,}$

wobei die Cartan-Subalgebra die Spanne von ist . Sei definiert durch für eine beliebige komplexe Zahl . Dann wird der Verma-Modul mit dem höchsten Gewicht von linear unabhängigen Vektoren aufgespannt und die Wirkung der Basiselemente ist wie folgt: ${\displaystyle H}$${\displaystyle \lambda}$${\displaystyle \lambda(H)=m}$${\displaystyle m}$${\displaystyle \lambda}$${\displaystyle v_{0},v_{1},v_{2},\dots}$

${\displaystyle Y\cdot v_{j}=v_{j+1};\quad X\cdot v_{j}=j(m-(j-1))v_{j-1};\quad H\cdot v_{j}=(m-2j)v_{j}}$.

(Das bedeutet insbesondere that und that .) Diese Formeln sind motiviert durch die Wirkungsweise der Basiselemente in den endlich-dimensionalen Darstellungen von , außer dass wir nicht mehr verlangen, dass die "Kette" der Eigenvektoren für terminiert. ${\displaystyle H\cdot v_{0}=mv_{0}}$${\displaystyle X\cdot v_{0}=0}$${\displaystyle \mathrm{sl} (2;\mathbb{C})}$${\displaystyle H}$

In dieser Konstruktion ist eine beliebige komplexe Zahl, die nicht unbedingt reell oder positiv oder eine ganze Zahl ist. Nichtsdestotrotz ist der Fall, in dem eine nicht negative ganze Zahl ist, etwas Besonderes. In diesem Fall kann man leicht erkennen, dass die Spanne der Vektoren invariant ist – weil . Der Quotientenmodul ist dann die endlichdimensionale irreduzible Darstellung von Dimension${\displaystyle m}$${\displaystyle m}$${\displaystyle v_{m+1},v_{m+2},\ldots}$${\displaystyle X\cdot v_{m+1}=0}$${\displaystyle \mathrm{sl} (2;\mathbb{C})}$${\displaystyle m+1.}$

Definition der Verma-Module

Es gibt zwei Standardkonstruktionen des Verma-Moduls, die beide das Konzept der universellen Hüllalgebra beinhalten . Wir setzen die Notation des vorherigen Abschnitts fort: ist eine komplexe halbeinfache Lie-Algebra, ist eine feste Cartan-Subalgebra, ist das zugehörige Wurzelsystem mit einer festen Menge positiver Wurzeln. Für jedes wählen wir Elemente ungleich null und . ${\displaystyle {\mathfrak {g}}}$${\displaystyle {\mathfrak{h}}}$${\displaystyle R}$${\displaystyle R^{+}}$${\displaystyle \alpha\in R^{+}}$${\displaystyle X_{\alpha}\in {\mathfrak {g}}_{\alpha}}$${\displaystyle Y_{\alpha}\in {\mathfrak {g}}_{-\alpha}}$

Als Quotient der Hüllalgebra

Die erste Konstruktion des Verma-Moduls ist ein Quotient der universellen Hüllalgebra von . Da das Verma-Modul ein -Modul sein soll, wird es aufgrund der universellen Eigenschaft der einhüllenden Algebra auch ein -Modul sein. Wenn wir also ein Verma-Modul mit dem höchsten Gewichtungsvektor haben , gibt es eine lineare Abbildung von in gegeben durch ${\displaystyle U({\mathfrak{g}})}$${\displaystyle {\mathfrak {g}}}$${\displaystyle {\mathfrak {g}}}$${\displaystyle U({\mathfrak{g}})}$${\displaystyle W_{\lambda}}$${\displaystyle v}$${\displaystyle \Phi}$${\displaystyle U({\mathfrak{g}})}$${\displaystyle W_{\lambda}}$

${\displaystyle \Phi(x)=x\cdot v,\quad x\in U({\mathfrak{g}})}$.

Da von generiert werden soll , sollte die Karte surjektiv sein. Da es sich um einen Vektor mit dem höchsten Gewicht handeln soll, sollte der Kern von alle Wurzelvektoren für in enthalten . Da auch ein Gewichtungsvektor mit Gewicht sein soll , sollte der Kern von alle Vektoren der Form ${\displaystyle W_{\lambda}}$${\displaystyle v}$${\displaystyle \Phi}$${\displaystyle v}$${\displaystyle \Phi}$${\displaystyle X_{\alpha}}$${\displaystyle\alpha}$${\displaystyle R^{+}}$${\displaystyle v}$${\displaystyle \lambda}$${\displaystyle \Phi}$

${\displaystyle H-\lambda(H)1,\quad H\in{\mathfrak{h}}}$.

Schließlich sollte der Kern von ein linkes Ideal in sein ; schließlich, wenn dann für alle . ${\displaystyle \Phi}$${\displaystyle U({\mathfrak{g}})}$${\displaystyle x\cdot v=0}$${\displaystyle (yx)\cdot v=y\cdot (x\cdot v)=0}$${\displaystyle y\in U({\mathfrak{g}})}$

Die vorangegangene Diskussion motiviert die folgende Konstruktion des Verma-Moduls. Wir definieren als Quotientenvektorraum ${\displaystyle W_{\lambda}}$

${\displaystyle W_{\lambda}=U({\mathfrak{g}})/I_{\lambda}}$,

wo ist das linke Ideal, das von allen Elementen der Form erzeugt wird ${\displaystyle I_{\lambda}}$

${\displaystyle X_{\alpha},\quad\alpha\in R^{+},}$

und

${\displaystyle H-\lambda(H)1,\quad H\in{\mathfrak{h}}}$.

Da es sich um ein Linksideal handelt, überträgt sich die natürliche Linkswirkung auf sich selbst auf den Quotienten. Also ist ein -Modul und damit auch ein -Modul. ${\displaystyle I_{\lambda}}$${\displaystyle U({\mathfrak{g}})}$${\displaystyle W_{\lambda}}$${\displaystyle U({\mathfrak{g}})}$${\displaystyle {\mathfrak {g}}}$

Durch Erweiterung von Skalaren

Die Prozedur " Erweiterung von Skalaren " ist ein Verfahren zum Ändern eines linken Moduls über einer (nicht unbedingt kommutativen) Algebra in ein linkes Modul über einer größeren Algebra , die als Subalgebra enthält . Wir können uns einen Rechts- Modul vorstellen, bei dem durch Multiplikation auf das Recht einwirkt . Da ist ein Links- Modul und ist ein Rechts- Modul, können wir das Tensorprodukt der beiden über die Algebra bilden : ${\displaystyle V}$${\displaystyle A_{1}}$${\displaystyle A_{2}}$${\displaystyle A_{1}}$${\displaystyle A_{2}}$${\displaystyle A_{1}}$${\displaystyle A_{1}}$${\displaystyle A_{2}}$${\displaystyle V}$${\displaystyle A_{1}}$${\displaystyle A_{2}}$${\displaystyle A_{1}}$${\displaystyle A_{1}}$

${\displaystyle A_{2}\otimes_{A_{1}}V}$.

Da nun ein linker -Modul über sich selbst ist, trägt das obige Tensorprodukt eine linke Modulstruktur über der größeren Algebra , die eindeutig durch die Forderung bestimmt wird, dass ${\displaystyle A_{2}}$${\displaystyle A_{2}}$${\displaystyle A_{2}}$

${\displaystyle a_{1}\cdot (a_{2}\otimes v)=(a_{1}a_{2})\otimes v}$

für alle und in . Somit haben wir ausgehend vom left- Modul ein left- Modul erzeugt . ${\displaystyle a_{1}}$${\displaystyle a_{2}}$${\displaystyle A_{2}}$${\displaystyle A_{1}}$${\displaystyle V}$${\displaystyle A_{2}}$${\displaystyle A_{2}\otimes_{A_{1}}V}$

Wir wenden diese Konstruktion nun im Rahmen einer halbeinfachen Lie-Algebra an. Wir seien die Subalgebra von aufgespannt von und die Wurzelvektoren mit . (Ist also eine "Borel-Subalgebra" von .) Wir können ein linkes Modul über der universellen Hüllalgebra wie folgt bilden: ${\displaystyle {\mathfrak {b}}}$${\displaystyle {\mathfrak {g}}}$${\displaystyle {\mathfrak{h}}}$${\displaystyle X_{\alpha}}$${\displaystyle \alpha\in R^{+}}$${\displaystyle {\mathfrak {b}}}$${\displaystyle {\mathfrak {g}}}$${\displaystyle F_{\lambda}}$${\displaystyle U({\mathfrak {b}})}$

• ${\displaystyle F_{\lambda}}$ist der eindimensionale Vektorraum, der von einem einzelnen Vektor zusammen mit einer - Modulstruktur aufgespannt wird, so dass die Multiplikation mit und die positiven Wurzelräume trivial wirken:${\displaystyle v}$${\displaystyle {\mathfrak {b}}}$${\displaystyle {\mathfrak{h}}}$${\displaystyle \lambda}$

${\displaystyle \quad H\cdot v=\lambda(H)v,\quad H\in {\mathfrak{h}};\quad X_{\alpha}\cdot v=0,\quad\alpha\in R ^{+}}$.

Die Motivation für diese Formel ist, dass sie beschreibt, wie auf den höchsten Gewichtsvektor in einem Verma-Modul wirken soll. ${\displaystyle U({\mathfrak {b}})}$

Aus dem Satz von Poincaré-Birkhoff-Witt folgt nun, dass eine Subalgebra von ist . Daher können wir die Erweiterung der Skalartechnik anwenden, um von einem linken -Modul in ein linkes -Modul wie folgt umzuwandeln : ${\displaystyle U({\mathfrak {b}})}$${\displaystyle U({\mathfrak{g}})}$${\displaystyle F_{\lambda}}$${\displaystyle U({\mathfrak {b}})}$${\displaystyle U({\mathfrak{g}})}$${\displaystyle W_{\lambda}}$

${\displaystyle W_{\lambda}:=U({\mathfrak{g}})\otimes_{U({\mathfrak{b}})}F_{\lambda}}$.

Da es sich um ein linkes -Modul handelt, ist es insbesondere ein Modul (Repräsentation) für . ${\displaystyle W_{\lambda}}$${\displaystyle U({\mathfrak{g}})}$${\displaystyle {\mathfrak {g}}}$

Der Aufbau des Verma-Moduls

Welche Konstruktion des Verma-Moduls auch immer verwendet wird, man muss beweisen, dass es nicht trivial ist, dh nicht das Nullmodul. Tatsächlich ist es möglich, den Satz von Poincaré-Birkhoff-Witt zu verwenden, um zu zeigen, dass der zugrunde liegende Vektorraum von isomorph zu ${\displaystyle W_{\lambda}}$

${\displaystyle U({\mathfrak {g}}_{-})}$

wo ist die Lie-Subalgebra, die von den negativen Wurzelräumen von (d. h. den 's) erzeugt wird. ${\displaystyle {\mathfrak {g}}_{-}}$${\displaystyle {\mathfrak {g}}}$${\displaystyle Y_{\alpha}}$

Grundeigenschaften

Verma Module, gilt als - Module sind höchste Gewicht Module , dh sie werden von einem erzeugten höchsten Gewichtsvektor . Diese höchste Gewichtsvektor ist (der erste ist die Einheit , in und die zweite ist die Einheit in dem Bereich , betrachtet als - Modul ) , und es hat Gewicht . ${\displaystyle {\mathfrak {g}}}$${\displaystyle 1\otimes 1}$${\displaystyle 1}$${\displaystyle {\mathcal{U}}({\mathfrak{g}})}$${\displaystyle F}$${\displaystyle {\mathfrak {b}}}$ ${\displaystyle F_{\lambda}}$${\displaystyle \lambda}$

Vielfältigkeit

Verma Module sind Gewichtsmodule , dh eine direkte Summe aller seiner Gewichtsräume . Jeder Gewichtsraum in ist endlichdimensional und die Dimension des -Gewichtsraums ist die Anzahl der Möglichkeiten, sich als Summe positiver Wurzeln auszudrücken (dies steht in engem Zusammenhang mit der sogenannten Kostanten Teilungsfunktion ). Diese Behauptung folgt aus der früheren Behauptung, dass der Verma-Modul als Vektorraum zu isomorph ist , zusammen mit dem Poincaré-Birkhoff-Witt-Theorem für . ${\displaystyle W_{\lambda}}$${\displaystyle W_{\lambda}}$${\displaystyle\mu}$${\displaystyle W_{\mu}}$${\displaystyle \lambda -\mu}$${\displaystyle U({\mathfrak {g}}_{-})}$${\displaystyle U({\mathfrak {g}}_{-})}$

Universelles Eigentum

Verma Module hat eine sehr wichtige Eigenschaft: Wenn irgendeine Darstellung von einem höchsten Gewichtsvektor von Gewicht erzeugt , gibt es einen surjektiven - Homomorphismus Das heißt, alle Darstellungen mit höchstem Gewicht , die durch den höchsten Gewichtsvektor erzeugt werden (so genannte höchstes Gewicht Module ) sind Quotienten von${\displaystyle V}$${\displaystyle \lambda}$ ${\displaystyle {\mathfrak {g}}}$ ${\displaystyle W_{\lambda}\to V.}$${\displaystyle \lambda}$${\displaystyle W_{\lambda}.}$

Irreduzibler Quotientenmodul

${\displaystyle W_{\lambda}}$enthält einen eindeutigen maximalen Untermodul , und sein Quotient ist die (bis auf Isomorphie ) eindeutige irreduzible Darstellung mit höchstem Gewicht. Wenn das höchste Gewicht dominant und ganzzahlig ist, dann beweist man, dass dieser irreduzible Quotient tatsächlich endlichdimensional ist. ${\displaystyle \lambda.}$${\displaystyle \lambda}$

Betrachten Sie als Beispiel den oben diskutierten Fall . Wenn das höchste Gewicht ein "dominantes Integral" ist – was einfach bedeutet, dass es eine nicht negative ganze Zahl ist – dann ist die Spanne der Elemente invariant. Die Quotientendarstellung ist dann mit Dimension irreduzibel . Die Quotientendarstellung wird von linear unabhängigen Vektoren aufgespannt . Die Wirkung von ist die gleiche wie im Verma-Modul, außer dass im Quotienten im Vergleich zum Verma-Modul. ${\displaystyle {\mathfrak {g}}=\operatorname {sl} (2;\mathbb {C})}$${\displaystyle m}$${\displaystyle Xv_{m+1}=0}$${\displaystyle v_{m+1},v_{m+2},\ldots}$${\displaystyle m+1}$${\displaystyle v_{0},v_{1},\ldots ,v_{m}}$${\displaystyle \operatorname {sl} (2;\mathbb {C} )}$${\displaystyle Yv_{m}=0}$${\displaystyle Yv_{m}=v_{m+1}}$

Das Verma-Modul selbst ist genau dann irreduzibel, wenn keine der Koordinaten von in der Basis der Fundamentalgewichte aus der Menge stammt . ${\displaystyle W_{\lambda}}$${\displaystyle \lambda}$${\displaystyle \{0,1,2,\ldots\}}$

Andere Eigenschaften

Das Verma-Modul heißt regulär , wenn sein höchstes Gewicht λ auf der affinen Weyl-Bahn eines dominanten Gewichts liegt . Mit anderen Worten, es gibt ein Element w der Weyl-Gruppe W mit ${\displaystyle W_{\lambda}}$${\displaystyle {\tilde {\lambda}}}$

${\displaystyle \lambda =w\cdot {\tilde {\lambda}}}$

wo ist die affine Wirkung der Weyl-Gruppe . ${\displaystyle \cdot}$

Das Verma-Modul heißt singulär , wenn es kein dominantes Gewicht auf der affinen Bahn von gibt. In diesem Fall ist ein Gewicht gibt es so , dass an der Wand der ist fundamental Weyl Kammer (δ ist die Summe aller grundlegenden Gewichte ). ${\displaystyle W_{\lambda}}$${\displaystyle {\tilde {\lambda}}}$${\displaystyle {\tilde {\lambda}}+\delta}$

Homomorphismen von Verma-Modulen

Für zwei beliebige Gewichte ein nichttrivialer Homomorphismus${\displaystyle \lambda,\mu}$

${\displaystyle W_{\mu}\rightarrow W_{\lambda}}$

können nur existieren, wenn und mit einer affinen Wirkung der Weyl-Gruppe der Lie-Algebra verbunden sind . Dies folgt leicht aus dem Harish-Chandra-Theorem über infinitesimale Zentralzeichen . ${\displaystyle\mu}$${\displaystyle \lambda}$ ${\displaystyle W}$${\displaystyle {\mathfrak {g}}}$

Jeder Homomorphismus von Verma-Modulen ist injektiv und die Dimension

${\displaystyle \dim(\operatorname {Hom} (W_{\mu},W_{\lambda}))\leq 1}$

für irgendwelche . So gibt es eine Nicht - Null , wenn und nur wenn ist isomorph zu einem (einmaligen) Submodul . ${\displaystyle\mu,\lambda}$${\displaystyle W_{\mu}\rightarrow W_{\lambda}}$${\displaystyle W_{\mu}}$${\displaystyle W_{\lambda}}$

Die vollständige Klassifikation der Verma-Modulhomomorphismen wurde von Bernstein–Gelfand–Gelfand und Verma vorgenommen und kann in der folgenden Aussage zusammengefasst werden:

Es existiert genau dann ein Homomorphismus ungleich Null, wenn es existiert ${\displaystyle W_{\mu}\rightarrow W_{\lambda}}$

eine Folge von Gewichten

${\displaystyle\mu=\nu_{0}\leq\nu_{1}\leq\ldots\leq\nu_{k}=\lambda}$

so dass für einige positive Wurzeln (und ist die entsprechende Wurzelreflexion und ist die Summe aller Fundamentalgewichte ) und für jede eine natürliche Zahl ( ist die mit der Wurzel verbundene Kowurzel ).${\displaystyle \nu_{i-1}+\delta =s_{\gamma_{i}}(\nu_{i}+\delta)}$${\displaystyle \gamma_{i}}$${\displaystyle s_{\gamma_{i}}}$${\displaystyle\delta}$${\displaystyle 1\leq i\leq k,(\nu_{i}+\delta)(H_{\gamma_{i}})}$${\displaystyle H_{\gamma_{i}}}$${\displaystyle \gamma_{i}}$

Wenn die Module Verma und sind regelmäßig , so gibt es ein einzigartiges dominierendes Gewicht und einzigartige Elemente w , w 'der Weyl - Gruppe W , so dass ${\displaystyle M_{\mu}}$${\displaystyle M_{\lambda}}$ ${\displaystyle {\tilde {\lambda}}}$

${\displaystyle \mu =w'\cdot {\tilde {\lambda}}}$

und

${\displaystyle \lambda =w\cdot {\tilde {\lambda}},}$

wo ist die affine Wirkung der Weyl-Gruppe. Sind die Gewichte weiter ganzzahlig , dann existiert ein Homomorphismus ungleich Null ${\displaystyle \cdot}$

${\displaystyle W_{\mu}\to W_{\lambda}}$

dann und nur dann, wenn

${\displaystyle w\leq w'}$

in der Bruhat-Ordnung der Weyl-Gruppe.

Jordan–Hölder-Reihe

Lassen

${\displaystyle 0\subset A\subset B\subset W_{\lambda}}$

eine Folge von -Modulen sein, so dass der Quotient B/A mit dem höchsten Gewicht μ irreduzibel ist . Dann existiert ein Homomorphismus ungleich Null . ${\displaystyle {\mathfrak {g}}}$${\displaystyle W_{\mu}\to W_{\lambda}}$

Eine einfache Konsequenz daraus ist, dass für alle Module mit dem höchsten Gewicht, so dass ${\displaystyle V_{\mu},V_{\lambda}}$

${\displaystyle V_{\mu}\subset V_{\lambda}}$

es existiert ein Homomorphismus ungleich Null . ${\displaystyle W_{\mu}\to W_{\lambda}}$

Bernstein–Gelfand–Gelfand-Auflösung

Sei eine endlichdimensionale irreduzible Darstellung der Lie-Algebra mit dem höchsten Gewicht λ. Aus dem Abschnitt über Homomorphismen von Verma-Modulen wissen wir, dass es einen Homomorphismus gibt ${\displaystyle V_{\lambda}}$ ${\displaystyle {\mathfrak {g}}}$

${\displaystyle W_{w'\cdot\lambda}\to W_{w\cdot\lambda}}$

dann und nur dann, wenn

${\displaystyle w\leq w'}$

in der Bruhat-Ordnung der Weyl-Gruppe . Der folgende Satz beschreibt eine Auflösung von in Verma-Modulen (er wurde 1975 von Bernstein – Gelfand – Gelfand bewiesen ): ${\displaystyle V_{\lambda}}$

Es existiert eine exakte Folge von -Homomorphismen ${\displaystyle {\mathfrak {g}}}$

${\displaystyle 0\to\oplus_{w\in W,\,\,\ell(w)=n}W_{w\cdot\lambda}\to\cdots\to \oplus_{w\in W, \,\,\ell (w)=2}W_{w\cdot \lambda }\to \oplus _{w\in W,\,\,\ell (w)=1}W_{w\cdot \lambda }\to W_{\lambda}\to V_{\lambda}\to 0}$

wobei n die Länge des größten Elements der Weyl-Gruppe ist.

Eine ähnliche Auflösung existiert auch für verallgemeinerte Verma-Module . Er wird kurz als BGG-Beschluss bezeichnet .

Siehe auch

• Klassifizieren endlich-dimensionaler Darstellungen von Lie-Algebren
• Satz vom höchsten Gewicht
• Generalisiertes Verma-Modul
• Weyl-Modul

Anmerkungen

Verweise

• Bäuerle, GGA; de Kerf, EA; ten Kroode, APE (1997). A. van Groesen; EM de Jäger (Hrsg.). Endliche und unendlichdimensionale Lie-Algebren und ihre Anwendung in der Physik . Studium der mathematischen Physik. 7 . Nordholland. Kapitel 20. ISBN 978-0-444-82836-1– über ScienceDirect .
• Carter, R. (2005), Lie Algebras of Finite and Affin Type , Cambridge University Press, ISBN 978-0-521-85138-1.
• Dixmier, J. (1977), Enveloping Algebras , Amsterdam, New York, Oxford: Nordholland, ISBN 978-0-444-11077-0.
• Hall, Brian C. (2015), Lie Groups, Lie Algebras, and Representations: An Elementary Introduction , Graduate Texts in Mathematics, 222 (2. Aufl.), Springer, ISBN 978-3319134666
• Humphreys, J. (1980), Einführung in die Lügenalgebren und Darstellungstheorie , Springer Verlag, ISBN 978-3-540-90052-8.
• Knapp, AW (2002), Lie Groups Beyond eine Einführung (2. Aufl.), Birkhäuser, p. 285, ISBN 978-0-8176-3926-6.
• Rocha, Alvany (2001) [1994], "BGG Resolution" , Encyclopedia of Mathematics , EMS Press
• Roggenkamp, ​​K.; Stefanescu, M. (2002), Algebra - Darstellungstheorie , Springer, ISBN 978-0-7923-7114-4.

Dieser Artikel enthält Material aus dem Verma-Modul auf PlanetMath , das unter der Creative Commons-Lizenz Namensnennung/Weitergabe unter gleichen Bedingungen lizenziert ist .