Farey-Sequenz - Farey sequence

Farey-Diagramm zu F ₉ mit Kreisbögen dargestellt. Bewegen Sie den Mauszeiger im SVG-Bild über eine Kurve, um sie und ihre Begriffe hervorzuheben.

Farey-Diagramm zu F ₉ .

Symmetrisches Muster aus den Nennern der Farey-Folge, F ₉ .

Symmetrisches Muster aus den Nennern der Farey-Folge, F ₂₅ .

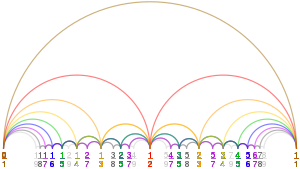
In der Mathematik , die Farey - Sequenz der Ordnung n ist die Sequenz von vollständig reduzierten Fraktionen , entweder zwischen 0 und 1 ist , oder ohne diese Einschränkung, die , wenn sie in niedrigsten Begriffen haben Nenner weniger als oder gleich n , in der Reihenfolge zunehmender Größe angeordnet ist .

Bei der eingeschränkten Definition beginnt jede Farey-Folge mit dem Wert 0, gekennzeichnet durch den Bruch 0/1, und endet mit dem Wert 1, gekennzeichnet durch den Bruch 1/1 (obwohl einige Autoren diese Begriffe weglassen).

Eine Farey-Folge wird manchmal als Farey- Reihe bezeichnet , was nicht ganz korrekt ist, da die Terme nicht summiert werden.

Beispiele

Die Farey-Reihenfolgen der Ordnungen 1 bis 8 sind:

F ₁ = {0/1_, 1/1 }

F ₂ = {0/1_, 1/2_, 1/1 }

F ₃ = {0/1_, 1/3_, 1/2_, 2/3_, 1/1 }

F ₄ = {0/1_, 1/4_, 1/3_, 1/2_, 2/3_, 3/4_, 1/1 }

F ₅ = {0/1_, 1/5_, 1/4_, 1/3_, 2/5_, 1/2_, 3/5_, 2/3_, 3/4_, 4/5_, 1/1 }

F ₆ = {0/1_, 1/6_, 1/5_, 1/4_, 1/3_, 2/5_, 1/2_, 3/5_, 2/3_, 3/4_, 4/5_, 5/6_, 1/1 }

F ₇ = {0/1_, 1/7_, 1/6_, 1/5_, 1/4_, 2/7_, 1/3_, 2/5_, 3/7_, 1/2_, 4/7_, 3/5_, 2/3_, 5/7_, 3/4_, 4/5_, 5/6_, 6/7_, 1/1 }

F ₈ = {0/1_, 1/8_, 1/7_, 1/6_, 1/5_, 1/4_, 2/7_, 1/3_, 3/8_, 2/5_, 3/7_, 1/2_, 4/7_, 3/5_, 5/8_, 2/3_, 5/7_, 3/4_, 4/5_, 5/6_, 6/7_, 7/8_, 1/1 }

 F1 = {0/1, 1/1}
 F2 = {0/1, 1/2, 1/1}
 F3 = {0/1, 1/3, 1/2, 2/3, 1/1}
 F4 = {0/1, 1/4, 1/3, 1/2, 2/3, 3/4, 1/1}
 F5 = {0/1, 1/5, 1/4, 1/3, 2/5, 1/2, 3/5, 2/3, 3/4, 4/5, 1/1}
 F6 = {0/1, 1/6, 1/5, 1/4, 1/3, 2/5, 1/2, 3/5, 2/3, 3/4, 4/5, 5/6 , 1/1}
 F7 = {0/1, 1/7, 1/6, 1/5, 1/4, 2/7, 1/3, 2/5, 3/7, 1/2, 4/7, 3/5 , 2/3, 5/7, 3/4, 4/5, 5/6, 6/7, 1/1}
 F8 = {0/1, 1/8, 1/7, 1/6, 1/5, 1/4, 2/7, 1/3, 3/8, 2/5, 3/7, 1/2 , 4/7, 3/5, 5/8, 2/3, 5/7, 3/4, 4/5, 5/6, 6/7, 7/8, 1/1}

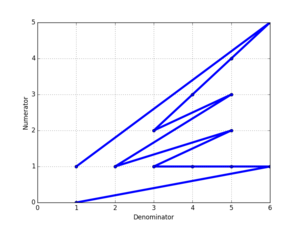
Wenn man die Zähler gegen die Nenner einer Farey-Folge aufträgt, erhält man eine Form wie rechts, gezeigt für F ₆ .

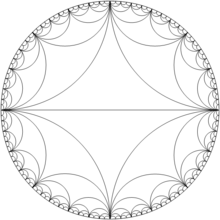
Das Reflektieren dieser Form um die Diagonal- und Hauptachse erzeugt den unten gezeigten Farey-Sonnendurchbruch . Der Farey-Sunburst der Ordnung n verbindet die sichtbaren ganzzahligen Gitterpunkte vom Ursprung im Quadrat der Seite 2 n , im Ursprung zentriert. Unter Verwendung des Satzes von Pick beträgt die Fläche des Sonnendurchbruchs 4(| F _n |−1), wobei | F _n | ist die Anzahl der Brüche in F _n .

Geschichte

Die Geschichte der 'Farey-Serie' ist sehr kurios — Hardy & Wright (1979)

... wieder einmal war der Mann, dessen Namen einer mathematischen Beziehung gegeben wurde, nach den Aufzeichnungen nicht der ursprüngliche Entdecker. — Beiler (1964)

Farey - Sequenzen werden nach dem Namen britischen Geologen John Farey, Sr. , dessen Brief über diese Sequenzen wurde in der veröffentlichten Philosophical Magazine in 1816. Farey gemutmaßt, ohne Opfer Beweis, dass jeder neue Begriff in einer Farey Folge Expansion ist die mediant seiner Nachbarn . Fareys Brief wurde von Cauchy gelesen , der in seinen Exercices de mathématique einen Beweis lieferte und dieses Ergebnis Farey zuschrieb. Tatsächlich hatte ein anderer Mathematiker, Charles Haros , 1802 ähnliche Ergebnisse veröffentlicht, die weder Farey noch Cauchy bekannt waren. Es war also ein historischer Zufall, der Fareys Namen mit diesen Sequenzen verband. Dies ist ein Beispiel für das Stiglersche Gesetz der Namensgebung .

Eigenschaften

Sequenzlänge und Index eines Bruchs

Die Farey-Folge der Ordnung n enthält alle Mitglieder der Farey-Folgen niedrigerer Ordnung. Insbesondere enthält F _n alle Glieder von F _{n -1} und enthält auch einen zusätzlichen Bruch für jede Zahl, die kleiner als n ist und zu n teilerfremd ist . Somit besteht F ₆ aus F ₅ zusammen mit den Brüchen1/6 und 5/6.

Der mittlere Term einer Farey-Folge F _n ist immer1/2, für n > 1. Daraus können wir die Längen von F _n und F _{n −1} mit der Eulerschen Totient-Funktion in Beziehung setzen  : ${\displaystyle\varphi(n)}$

${\displaystyle |F_{n}|=|F_{n-1}|+\varphi(n).}$

Ausgehend von der Tatsache, dass | F ₁ | = 2, können wir einen Ausdruck für die Länge von F _n herleiten :

${\displaystyle |F_{n}|=1+\sum_{m=1}^{n}\varphi(m)=1+\Phi(n),}$

wo ist der summative totient . ${\displaystyle \Phi(n)}$

Wir haben auch :

${\displaystyle |F_{n}|={\frac {1}{2}}\left(3+\sum_{d=1}^{n}\mu(d)\left\lfloor {\tfrac { n}{d}}\right\rfloor ^{2}\right),}$

und durch eine Möbius-Inversionsformel  :

${\displaystyle |F_{n}|={\frac {1}{2}}(n+3)n-\sum _{d=2}^{n}|F_{\lfloor n/d\rfloor} |,}$

wobei µ( d ) die zahlentheoretische Möbius-Funktion und die Bodenfunktion ist . ${\displaystyle \lfloor {\tfrac {n}{d}}\rfloor}$

Das asymptotische Verhalten von | F _n | ist :

${\displaystyle |F_{n}|\sim {\frac {3n^{2}}{\pi^{2}}}.}$

Der Index eines Bruchs in der Farey-Folge ist einfach die Position, die in der Folge eingenommen wird. Dies ist von besonderer Relevanz, da es in einer alternativen Formulierung der Riemann-Hypothese verwendet wird , siehe unten . Es folgen verschiedene nützliche Eigenschaften: ${\displaystyle I_{n}(a_{k,n})=k}$${\displaystyle a_{k,n}}$${\displaystyle F_{n}=\{a_{k,n}:k=0,1,\ldots,m_{n}\}}$${\displaystyle a_{k,n}}$

${\displaystyle I_{n}(0/1)=0,}$

${\displaystyle I_{n}(1/n)=1,}$

${\displaystyle I_{n}(1/2)=(|F_{n}|-1)/2,}$

${\displaystyle I_{n}(1/1)=|F_{n}|-1,}$

${\displaystyle I_{n}(h/k)=|F_{n}|-1-I_{n}((kh)/k).}$

Der Index von where und ist das kleinste gemeinsame Vielfache der ersten Zahlen, , ist gegeben durch: ${\displaystyle 1/k}$${\displaystyle n/(i+1)<k\leq n/i}$${\displaystyle n}$${\displaystyle i}$${\displaystyle n={\rm {lcm}}([2,i])}$

${\displaystyle I_{n}(1/k)=1+n\sum_{j=1}^{i}{\frac {\varphi (j)}{j}}-k\Phi (i). }$

Farey Nachbarn

Brüche, die benachbarte Terme in einer beliebigen Farey-Folge sind, werden als Farey-Paar bezeichnet und haben die folgenden Eigenschaften.

Ob ein/B und C/D sind Nachbarn in einer Farey-Sequenz, mit ein/B < C/D, dann ihr Unterschied C/D − ein/B entspricht 1/bd. Dies liegt daran, dass jedes aufeinanderfolgende Paar von Farey-Rationalen eine äquivalente Fläche von 1 hat.

Wenn r1=p/q und r2=p'/q' als Vektoren (p,q) in der x,y-Ebene interpretiert werden, ist die Fläche von A(p/q,p'/q') gegeben durch qp' - q'p. Da jeder hinzugefügte Bruch zwischen zwei vorherigen aufeinanderfolgenden Fraktionen der Farey-Sequenz als Medianwert (⊕) berechnet wird

A(r1,r1⊕r2) = A(r1,r1) + A(r1,r2) = A(r1,r2) = 1 (da r1=1/0 und r2=0/1 sein muss, muss seine Fläche eins sein) .

Seit:${\displaystyle {\frac {c}{d}}-{\frac {a}{b}}={\frac {bc-ad}{bd}},}$

das ist gleichbedeutend damit, das zu sagen

${\displaystyle bc-ad=1}$.

Daher 1/3 und 2/5sind Nachbarn in F ₅ , und ihr Unterschied ist1/fünfzehn.

Das Umgekehrte gilt auch. Ob

${\displaystyle bc-ad=1}$

für positive ganze Zahlen a , b , c und d mit a < b und c < d dannein/B und C/Dwerden Nachbarn in der Farey-Folge der Ordnung max( b, d ).

Ob P/Q hat Nachbarn ein/B und C/D in einer Farey-Sequenz, mit

${\displaystyle {\frac {a}{b}}<{\frac {p}{q}}<{\frac {c}{d}}}$

dann P/Qist der Median vonein/B und C/D - mit anderen Worten,

${\displaystyle {\frac {p}{q}}={\frac {a+c}{b+d}}.}$

Dies folgt leicht aus der vorherigen Eigenschaft, denn wenn bp – aq = qc – pd = 1 , dann bp + pd = qc + aq , p ( b + d ) = q ( a + c ) ,P/Q = a + c/b + d.

Daraus folgt, dass wenn ein/B und C/D Nachbarn in einer Farey-Folge sind, dann ist der erste Term, der zwischen ihnen erscheint, wenn die Reihenfolge der Farey-Folge erhöht wird,

${\displaystyle {\frac {a+c}{b+d}},}$

die zuerst in der Farey-Folge der Ordnung b + d auftritt .

Somit erscheint der erste Term zwischen 1/3 und 2/5 ist 3/8, das in F _{8 erscheint} .

Die Gesamtzahl von Farey-Nachbarpaaren in F _n beträgt 2|F _n |-3.

Der Stern-Brocot-Baum ist eine Datenstruktur, die zeigt, wie die Sequenz von 0 (=0/1) und 1 (= 1/1), indem aufeinanderfolgende Medianten genommen werden.

Farey Nachbarn und Kettenbrüche

Brüche, die als Nachbarn in einer Farey-Folge auftreten, haben eng verwandte Kettenbruchentwicklungen . Jeder Bruch hat zwei Kettenbruchentwicklungen – in einer ist der letzte Term 1; im anderen ist der letzte Term größer als 1. WennP/Q, die zuerst in der Farey-Folge F _{q vorkommt} , hat Kettenbruchentwicklungen

[0; a ₁ , a ₂ , ..., a _{n − 1} , a _n , 1]

[0; a ₁ , a ₂ , ..., a _{n − 1} , a _n + 1]

dann der nächste Nachbar von P/Qin F _q (das sein Nachbar mit dem größeren Nenner sein wird) hat eine Kettenbruchentwicklung

[0; a ₁ , a ₂ , ..., a _n ]

und sein anderer Nachbar hat eine kontinuierliche Bruchteilexpansion

[0; a ₁ , a ₂ , ..., a _{n − 1} ]

Beispielsweise, 3/8hat die beiden Kettenbruchentwicklungen [0; 2, 1, 1, 1] und [0; 2, 1, 2] , und seine Nachbarn in F ₈ sind2/5, die erweitert werden kann als [0; 2, 1, 1] ; und1/3, die erweitert werden kann als [0; 2, 1] .

Farey-Brüche und das kleinste gemeinsame Vielfache

Der lcm kann als Produkt von Farey-Bruchteilen ausgedrückt werden als

${\displaystyle {\text{lcm}}[1,2,...,N]=e^{\psi(N)}={\frac {1}{2}}\left(\prod_{r \in F_{N},0<r\leq 1/2}2\sin(\pi r)\right)^{2}}$

wo ist die zweite Chebyshev-Funktion . ${\displaystyle \psi (N)}$

Farey-Brüche und der größte gemeinsame Teiler

Da die Totientenfunktion des Euler direkt mit dem verbunden ist GCD so ist die Anzahl der Elemente in F _n ,

${\displaystyle |F_{n}|=1+\sum_{m=1}^{n}\varphi(m)=1+\sum\limits_{m=1}^{n}\sum\limits _{k=1}^{m}\gcd(k,m)\cos {2\pi {\frac {k}{m}}}.}$

Für beliebige 3 Farey-Brüche ein/B, C/D und e/Fdie folgende Identität zwischen den gcd 's der 2x2- Matrix-Determinanten im Absolutwert gilt:

${\displaystyle \gcd \left({\begin{Vmatrix}a&c\\b&d\end{Vmatrix}},{\begin{Vmatrix}a&e\\b&f\end{Vmatrix}}\right)=\gcd \left( {\begin{Vmatrix}a&c\\b&d\end{Vmatrix}},{\begin{Vmatrix}c&e\\d&f\end{Vmatrix}}\right)=\gcd \left({\begin{Vmatrix}a&e\ \b&f\end{Vmatrix}},{\begin{Vmatrix}c&e\\d&f\end{Vmatrix}}\right)}$

Anwendungen

Farey-Folgen sind sehr nützlich, um rationale Approximationen irrationaler Zahlen zu finden. Zum Beispiel verwendet Eliahous Konstruktion einer unteren Schranke für die Länge nichttrivialer Zyklen im 3 x +1-Prozess Farey-Folgen, um eine Kettenbruchentwicklung der Zahl log ₂ (3) zu berechnen .

In physikalischen Systemen mit Resonanzphänomenen bieten Farey-Sequenzen eine sehr elegante und effiziente Methode zur Berechnung von Resonanzorten in 1D und 2D.

Farey-Sequenzen spielen eine wichtige Rolle bei Studien der Bahnplanung mit beliebigem Winkel auf quadratischen Gittern, zum Beispiel bei der Charakterisierung ihrer Rechenkomplexität oder Optimalität. Die Verbindung kann als r- beschränkte Pfade betrachtet werden, nämlich Pfade, die aus Liniensegmenten bestehen, die jeweils höchstens Zeilen und höchstens Zellenspalten durchqueren . Sei die Menge der Vektoren, so dass , , und , teilerfremd sind. Sei das Ergebnis der Reflexion in der Linie . Lassen Sie . Dann kann jeder r- beschränkte Pfad als eine Folge von Vektoren aus beschrieben werden . Es gibt eine Bijektion zwischen und der Farey-Reihenfolge, die durch die Abbildung auf gegeben wird . ${\displaystyle r}$${\displaystyle r}$${\displaystyle Q}$${\displaystyle (q,p)}$${\displaystyle 1\leq q\leq r}$${\displaystyle 0\leq p\leq q}$${\displaystyle p}$${\displaystyle q}$${\displaystyle Q*}$${\displaystyle Q}$${\displaystyle y=x}$${\displaystyle S=\{(\pm x,\pm y):(x,y)\in Q\cup Q*\}}$${\displaystyle S}$${\displaystyle Q}$${\displaystyle r}$${\displaystyle (q,p)}$${\displaystyle {\tfrac {p}{q}}}$

Ford Kreise

Vergleich von Ford-Kreisen und einem Farey-Diagramm mit Kreisbögen für n von 1 bis 9. Jeder Bogen schneidet seine entsprechenden Kreise im rechten Winkel. Bewegen Sie den Mauszeiger im SVG-Bild über einen Kreis oder eine Kurve, um ihn und seine Begriffe hervorzuheben.

Es gibt eine Verbindung zwischen der Farey-Sequenz und den Ford-Kreisen .

Für jeden Bruch P/Q (in seinen niedrigsten Ausdrücken) gibt es einen Ford-Kreis C[P/Q], das ist der Kreis mit Radius 1/(2 q ² ) und Mittelpunkt bei (P/Q, 1/ 2 q ² ). Zwei Ford-Kreise für unterschiedliche Brüche sind entweder disjunkt oder tangential zueinander – zwei Ford-Kreise schneiden sich nie. Wenn 0 <P/Q < 1 dann die Ford-Kreise, die C[P/Q] sind genau die Ford-Kreise für Brüche, die Nachbarn von . sind P/Q in einer Farey-Sequenz.

Also C [2/5] ist tangential zu C [1/2], C [1/3], C [3/7], C [3/8] etc.

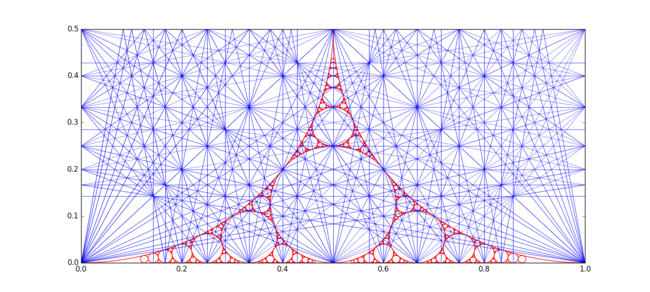
Ford-Kreise erscheinen auch in der apollinischen Dichtung (0,0,1,1). Das Bild unten veranschaulicht dies zusammen mit Farey-Resonanzlinien.

Apollonische Dichtung (0,0,1,1) und das Farey-Resonanzdiagramm.

Riemann-Hypothese

Farey-Sequenzen werden in zwei äquivalenten Formulierungen der Riemann-Hypothese verwendet . Angenommen, die Bedingungen von sind . Definiere , mit anderen Worten, ist die Differenz zwischen dem k- ten Term der n- ten Farey-Folge und dem k- ten Glied einer Menge der gleichen Anzahl von Punkten, gleichmäßig auf dem Einheitsintervall verteilt. 1924 bewies Jérôme Franel , dass die Aussage ${\displaystyle F_{n}}$${\displaystyle \{a_{k,n}:k=0,1,\ldots,m_{n}\}}$${\displaystyle d_{k,n}=a_{k,n}-k/m_{n}}$${\displaystyle d_{k,n}}$

${\displaystyle \sum_{k=1}^{m_{n}}d_{k,n}^{2}=O(n^{r})\quad \forall r>-1}$

entspricht der Riemann-Hypothese, und dann bemerkte Edmund Landau (direkt nach Franels Aufsatz), dass die Aussage

${\displaystyle \sum_{k=1}^{m_{n}}|d_{k,n}|=O(n^{r})\quad \forall r>1/2}$

ist auch äquivalent zur Riemann-Hypothese.

Andere Summen mit Farey-Bruchteilen

Die Summe aller Farey-Brüche der Ordnung n ist die halbe Anzahl der Elemente:

${\displaystyle \sum_{r\in F_{n}}r={\frac {1}{2}}|F_{n}|.}$

Die Summe der Nenner in der Farey-Folge ist das Doppelte der Summe der Zähler und bezieht sich auf die Eulersche Totient-Funktion:

${\displaystyle \sum_{a/b\in F_{n}}b=2\sum_{a/b\in F_{n}}a=1+\sum_{i=1}^{n} i\varphi (i),}$

was 1962 von Harold L. Aaron vermutet und 1966 von Jean A. Blake demonstriert wurde. Ein einzeiliger Beweis der Harold L. Aaron-Vermutung ist wie folgt. Die Summe der Zähler ist . Die Summe der Nenner ist . Der Quotient der ersten Summe zur zweiten Summe ist . ${\displaystyle {\displaystyle 1+\sum _{2\leq b\leq n}\sum _{(a,b)=1}a=1+\sum _{2\leq b\leq n}b{ \frac {\varphi(b)}{2}}}}$${\displaystyle {\displaystyle 2+\sum _{2\leq b\leq n}\sum _{(a,b)=1}b=2+\sum _{2\leq b\leq n}b\ varphi (b)}}$${\displaystyle {\frac {1}{2}}}$

Seien b _j die geordneten Nenner von F _n , dann gilt:

${\displaystyle \sum_{j=0}^{|F_{n}|-1}{\frac {b_{j}}{b_{j+1}}}={\frac {3|F_{n }|-4}{2}}}$

und

${\displaystyle \sum_{j=0}^{|F_{n}|-1}{\frac {1}{b_{j+1}b_{j}}}=1.}$

Sei a _j / b _j der j-te Farey-Bruch in F _n , dann

${\displaystyle \sum_{j=1}^{|F_{n}|-1}(a_{j-1}b_{j+1}-a_{j+1}b_{j-1})= \sum _{j=1}^{|F_{n}|-1}{\begin{Vmatrix}a_{j-1}&a_{j+1}\\b_{j-1}&b_{j+1 }\end{Vmatrix}}=3(|F_{n}|-1)-2n-1,}$

was in demonstriert wird. Auch nach dieser Referenz kann der Term innerhalb der Summe auf viele verschiedene Arten ausgedrückt werden:

${\displaystyle a_{j-1}b_{j+1}-a_{j+1}b_{j-1}={\frac {b_{j-1}+b_{j+1}}{b_{ j}}}={\frac {a_{j-1}+a_{j+1}}{a_{j}}}=\left\lfloor {\frac {n+b_{j-1}}{b_ {j}}}\right\rfloor ,}$

So erhält man viele verschiedene Summen über die Farey-Elemente mit dem gleichen Ergebnis. Mit der Symmetrie um 1/2 kann die ehemalige Summe auf die Hälfte der Folge begrenzt werden, da

${\displaystyle \sum_{j=1}^{\lfloor |F_{n}|/2\rfloor}(a_{j-1}b_{j+1}-a_{j+1}b_{j- 1})=3(|F_{n}|-1)/2-n-\lceil n/2\rceil ,}$

Die Mertens-Funktion kann als Summe über Farey-Brüche ausgedrückt werden als

${\displaystyle M(n)=-1+\sum_{a\in {\mathcal{F}}_{n}}e^{2\pi ia}}$   wo     ist die Farey-Folge der Ordnung n .${\displaystyle {\mathcal {F}}_{n}}$

Diese Formel wird im Beweis des Franel-Landau-Theorems verwendet .

Nächstes Semester

Es existiert ein überraschend einfacher Algorithmus, um die Terme von F _n entweder in traditioneller Reihenfolge (aufsteigend) oder nicht-traditioneller Reihenfolge (absteigend) zu erzeugen . Der Algorithmus berechnet jeden nachfolgenden Eintrag in Bezug auf die vorherigen zwei Einträge unter Verwendung der oben angegebenen Medianteneigenschaft. Obein/B und C/D sind die beiden angegebenen Einträge, und P/Q ist der unbekannte nächste Eintrag, dann C/D = a  +  p/b  +  q. SeitC/Din niedrigsten Begriffe ist, muss eine ganze Zahl sein k , so dass kc  =  a  +  p und kd  =  b  +  q , so dass p  =  kc  -  ein und q  =  kd  -  b . Betrachten wir p und q als Funktionen von k , dann

${\displaystyle {\frac {p(k)}{q(k)}}-{\frac {c}{d}}={\frac {cb-da}{d(kd-b)}}}$

je größer k wird, desto näherP/Q kommt an C/D.

Um den nächsten Term in der Folge anzugeben, muss k so groß wie möglich sein, vorbehaltlich kd  −  b  ≤  n (da wir nur Zahlen mit Nennern nicht größer als n betrachten ), also ist k die größte ganze Zahl ≤ n  +  b/D. Setzt man diesen Wert von k wieder in die Gleichungen für p und q ein, erhält man

${\displaystyle p=\left\lfloor {\frac {n+b}{d}}\right\rfloor ca}$

${\displaystyle q=\left\lfloor {\frac {n+b}{d}}\right\rfloor db}$

Dies ist in Python wie folgt implementiert :

def farey_sequence(n: int, descending: bool = False) -> None:
    """Print the n'th Farey sequence. Allow for either ascending or descending."""
    (a, b, c, d) = (0, 1, 1, n)
    if descending:
        (a, c) = (1, n - 1)
    print("{0}/{1}".format(a, b))
    while (c <= n and not descending) or (a > 0 and descending):
        k = (n + b) // d
        (a, b, c, d) = (c, d, k * c - a, k * d - b)
        print("{0}/{1}".format(a, b))

Brute-Force-Suchen nach Lösungen für diophantische Gleichungen in rationalen Zahlen können oft die Farey-Reihe nutzen (um nur reduzierte Formen zu suchen). Die mit (*) markierten Zeilen können auch so geändert werden, dass sie zwei benachbarte Terme enthalten, um Terme zu erzeugen, die nur größer (oder kleiner) als ein gegebener Term sind.

Siehe auch

• ABACABA-Muster
• Stern-Brocot-Baum
• Eulersche Totient-Funktion

Fußnoten

Verweise

Weiterlesen

• Hatcher, Allen . "Topologie der Zahlen" . Mathematik. Ithaka, NY: Cornell U.
• Graham, Ronald L. ; Knuth, Donald E. ; Pataschnik, Oren (1989). Konkrete Mathematik: Eine Grundlage für die Informatik (2. Aufl.). Boston, MA: Addison-Wesley. S. 115–123, 133–139, 150, 462–463, 523–524. ISBN 0-201-55802-5. — siehe insbesondere §4.5 (S. 115–123), Bonusaufgabe 4.61 (S. 150, 523–524), §4.9 (S. 133–139), §9.3, Aufgabe 9.3.6 (S. 462– 463).
• Vepstas, Linas. "Das Minkowski-Fragezeichen, GL(2,Z) und die Modulare Gruppe" (PDF) . — überprüft die Isomorphismen des Stern-Brocot Tree.
• Vepstas, Linas. "Symmetrien von Periodenverdopplungskarten" (PDF) . — überprüft Verbindungen zwischen Farey-Fraktionen und Fraktalen.
• Cobeli, Cristian; Zaharescu, Alexandru (2003). „Die Haros-Farey-Sequenz nach zweihundert Jahren. Eine Umfrage“. Acta Univ. Apulensis Math. Informieren. (5): 1–38. "S. 1–20" (PDF) . Acta Univ. Apulensis . "S. 21–38" (PDF) . Acta Univ. Apulensis .
• Matveev, Andrey O. (2017). Farey-Sequenzen: Dualität und Karten zwischen Untersequenzen . Berlin, DE: De Gruyter. ISBN 978-3-11-054662-0.

Externe Links

• Bogomolny, Alexander . "Farey-Serie" . Cut-the-Knoten .
• Bogomolny, Alexander . "Stern-Brocot-Baum" . Cut-the-Knoten .
• Pennestri, Ettore. "Ein Brocot-Tisch der Basis 120" .
• "Farey series" , Encyclopedia of Mathematics , EMS Press , 2001 [1994]
• Weisstein, Eric W. "Stern-Brocot Tree" . MathWorld .
• OEIS- Sequenz A005728 (Anzahl der Brüche in der Farey-Reihe der Ordnung n)
• OEIS- Sequenz A006842 (Zähler der Farey-Reihe der Ordnung n)
• OEIS- Sequenz A006843 (Nenner der Farey-Reihe der Ordnung n)
• Bonahon, Franz . Lustige Brüche und Ford-Kreise (Video). Brady Haran . Abgerufen am 9. Juni 2015 – über YouTube.