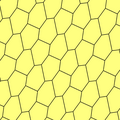
Sechseckige Fliesen - Hexagonal tiling

Sechseckige Fliesen

Typ	Normales Fliesenlegen
Vertex-Konfiguration	6.6.6 (oder 6 ³ )
Gesichtskonfiguration	V3.3.3.3.3.3 (oder V3 ⁶ )
Schläfli-Symbol(e)	{6,3} t{3,6}
Wythoff-Symbol(e)	3 \| 6 2 2 6 \| 3 3 3 3 \|
Coxeter-Diagramm(e)
Symmetrie	p6m , [6,3], (*632)
Rotationssymmetrie	p6 , [6,3] ⁺ , (632)
Dual	Dreieckige Fliesen
Eigenschaften	Scheitel-transitiv , kantentransitiv , flächentransitiv

In der Geometrie ist die hexagonale Kachelung oder hexagonale Tessellation eine regelmäßige Kachelung der Euklidischen Ebene , bei der sich an jedem Scheitelpunkt genau drei Sechsecke treffen. Es hat das Schläfli-Symbol von {6,3} oder t {3,6} (als abgeschnittene dreieckige Kachelung).

Der englische Mathematiker John Conway nannte es ein Hextille .

Der Innenwinkel des Sechsecks beträgt 120 Grad, so dass drei Sechsecke an einem Punkt volle 360 Grad ergeben. Es ist eine von drei regelmäßigen Kacheln des Flugzeugs . Die anderen beiden sind die dreieckigen und die quadratischen Fliesen .

Anwendungen

Die sechseckige Kachelung ist die dichteste Art , Kreise in zwei Dimensionen anzuordnen . Die Wabenvermutung besagt, dass die hexagonale Kachelung der beste Weg ist, um eine Fläche in Bereiche gleicher Fläche mit dem geringsten Gesamtumfang zu unterteilen. Die optimale dreidimensionale Struktur zur Herstellung von Waben (oder besser gesagt Seifenblasen) wurde von Lord Kelvin untersucht , der glaubte, dass die Kelvin-Struktur (oder das kubisch raumzentrierte Gitter) optimal ist. Die weniger regelmäßige Weaire-Phelan-Struktur ist jedoch etwas besser.

Diese Struktur existiert natürlicherweise in Form von Graphit , wobei jede Graphenschicht einem Hühnerdraht ähnelt, mit starken kovalenten Kohlenstoffbindungen. Röhrenförmige Graphenschichten wurden synthetisiert; diese werden als Kohlenstoff-Nanoröhrchen bezeichnet . Aufgrund ihrer hohen Zugfestigkeit und elektrischen Eigenschaften haben sie viele Anwendungsmöglichkeiten . Silicen ist ähnlich.

Hühnerdraht besteht aus einem sechseckigen Gitter (oft nicht regelmäßig) von Drähten.

Die dichteste Kreis Verpackung ist wie die Hexagone in diesen Kacheln angeordnet
Maschendraht Fechten
Graphen
Eine Kohlenstoff-Nanoröhrchen kann als eine sechseckige Kachelung auf einer zylindrischen Oberfläche betrachtet werden
Sechseckige persische Fliese um 1955

Die sechseckige Kachelung erscheint in vielen Kristallen. In drei Dimensionen sind die kubisch-flächenzentrierte und hexagonale dichte Packung übliche Kristallstrukturen. Sie sind die dichtesten Kugelpackungen in drei Dimensionen. Strukturell bestehen sie aus parallelen Schichten hexagonaler Kacheln, ähnlich der Struktur von Graphit. Sie unterscheiden sich darin, dass die Schichten gegeneinander versetzt sind, wobei der kubisch flächenzentrierte der beiden regelmäßiger ist. Reines Kupfer bildet unter anderem ein kubisch flächenzentriertes Gitter.

Einheitliche Färbungen

Es gibt drei unterschiedliche einheitliche Färbungen einer sechseckigen Kachelung, die alle aus der reflektierenden Symmetrie der Wythoff-Konstruktionen generiert wurden . Die ( h , k ) stellen die periodische Wiederholung einer farbigen Kachel dar, wobei die hexagonalen Abstände als h zuerst und k als zweites gezählt werden. Dieselbe Zählung wird in den Goldberg-Polyedern mit der Notation { p +,3} _{h , k verwendet} und kann auf hyperbolische Kacheln für p > 6 angewendet werden .

k-uniform	1-uniform			2-uniform		3-uniform
Symmetrie	p6m, (*632)		p3m1, (*333)	p6m, (*632)		S.6, (632)
Bild
Farben	1	2	3	2	4	2	7
(h,k)	(1,0)	(1,1)		(2,0)		(2,1)
Schläfli	{6,3}	t{3,6}	t{3 ^[3] }
Wythoff	3 \| 6 2	2 6 \| 3	3 3 3 \|
Coxeter
Conway	h	tΔ		cH=t6daH		wH=t6dsH

Die 3-farbige Kachelung ist eine Tesselation, die durch die Permutoeder der Ordnung 3 erzeugt wird .

Abgeschrägte sechseckige Fliesen

Eine abgeschrägte Sechskantfliese ersetzt Kanten durch neue Sechsecke und verwandelt sich in eine andere Sechskantfliese. In der Grenze verschwinden die ursprünglichen Flächen, und die neuen Sechsecke degenerieren zu Rauten, und es wird eine Rautenfliese .

Der abgeschrägte hexagonal tiling degeneriert in eine rhombille Fliese am Limit

Sechsecke (H)	Abgeschrägte Sechsecke (cH)			Rhombi (daH)

Zugehörige Fliesen

Die Sechsecke können in Sätze von 6 Dreiecken zerlegt werden. Dieser Vorgang führt zu zwei 2-gleichmäßigen Kacheln und der dreieckigen Kachelung :

Normales Fliesenlegen	Präparation	2-einheitliche Fliesen		Normales Fliesenlegen
Original		1/3 seziert	2/3 seziert	vollständig seziert
Regelmäßiges Fliesenlegen	Einsatz	2-Uniform Duals		Regelmäßiges Fliesenlegen
Original		1/3 Einschub	2/3 Einschub	vollständig eingelassen

Die hexagonale Kachelung kann als verlängerte rhombische Kachelung betrachtet werden , bei der jeder Scheitelpunkt der rhombischen Kachelung zu einer neuen Kante gedehnt wird. Dies ist ähnlich der Beziehung des rhombischen Dodekaeders und der rhombo-hexagonalen Dodekaeder- Tessellationen in 3 Dimensionen.

Rhombische Fliesen	Sechseckige Fliesen	Fechten nutzt diese Beziehung

Es ist auch möglich, die Prototile bestimmter sechseckiger Kacheln durch zwei, drei, vier oder neun gleiche Fünfecke zu unterteilen:

Fünfeckige Kachelung Typ 1 mit Überlagerungen von regelmäßigen Sechsecken (jeweils aus 2 Fünfecken).	Fünfeck-Kachelung Typ 3 mit Überlagerungen von regelmäßigen Sechsecken (jeweils aus 3 Fünfecken).	Fünfeckige Kachelung Typ 4 mit Überlagerungen von halbregelmäßigen Sechsecken (jeweils aus 4 Fünfecken).	Fünfeckige Kachelung Typ 3 mit Überlagerungen von zwei Größen regelmäßiger Sechsecke (bestehend aus 3 bzw. 9 Fünfecken).

Symmetriemutationen

Diese Kachelung ist topologisch verwandt als Teil einer Folge von regelmäßigen Kacheln mit hexagonalen Flächen, beginnend mit der hexagonalen Kachelung, mit Schläfli-Symbol {6,n} und Coxeter-Diagramm , fortschreitend ins Unendliche.

* n 62 Symmetriemutation von regulären Kacheln: {6, n } v T e
Sphärisch	Euklidisch	Hyperbolische Kacheln
{6,2}	{6,3}	{6,4}	{6,5}	{6,6}	{6,7}	{6,8}	...	{6,∞}

Diese Kachelung ist topologisch mit regulären Polyedern mit der Scheitelpunktfigur n ^{3 verwandt} , als Teil einer Sequenz, die sich in die hyperbolische Ebene fortsetzt .

* n 32 Symmetriemutation von regulären Kacheln: { n ,3} v T e
Sphärisch				Euklidisch	Kompakter Hyperb.		Parako.	Nicht kompakt hyperbolisch

{2,3}	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}	{12i,3}	{9i,3}	{6i,3}	{3i,3}

Ähnlich verhält es sich mit den gleichförmigen gestutzten Polyedern mit der Scheitelzahl n .6.6.

* n 32 Symmetriemutation von abgeschnittenen Kacheln: n .6.6 v T e
Sym. * N 42 [n, 3]	Sphärisch				Euklid.	Kompakt		Parak.	Nicht kompakt hyperbolisch
Sym. * N 42 [n, 3]	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]
Abgeschnittene Zahlen
Konfig.	2.6.6	3.6.6	4.6.6	5.6.6	6.6.6	7.6.6	8.6.6	.6.6	12i.6.6	9i.6.6	6i.6.6
n-kis- Figuren
Konfig.	V2.6.6	V3.6.6	V4.6.6	V5.6.6	V6.6.6	V7.6.6	V8.6.6	V∞.6.6	V12i.6.6	V9i.6.6	V6i.6.6

Diese Kachelung ist auch Teil einer Folge von abgeschnittenen rhombischen Polyedern und Kacheln mit [n,3] Coxeter-Gruppensymmetrie . Der Würfel kann als rhombisches Hexaeder angesehen werden, wobei die Rhomben Quadrate sind. Die abgeschnittenen Formen haben regelmäßige n-Ecke an den abgeschnittenen Scheitelpunkten und nicht regelmäßige sechseckige Flächen.

Symmetriemutationen dualer quasiregulärer Kacheln: V(3.n) ²
*n32	Sphärisch			Euklidisch	Hyperbolisch
*n32	*332	*432	*532	*632	*732	*832...	*∞32
Fliesen
Konf.	V(3.3) ²	V(3.4) ²	V(3.5) ²	V(3.6) ²	V(3.7) ²	V(3.8) ²	V(3.∞) ²

Wythoff Konstruktionen aus sechseckigen und dreieckigen Fliesen

Wie bei den gleichförmigen Polyedern gibt es acht gleichförmige Kacheln , die auf der regelmäßigen sechseckigen Kachelung (oder der dualen dreieckigen Kachelung ) basieren können .

Wenn man die Kacheln auf den ursprünglichen Flächen rot, gelb an den ursprünglichen Scheitelpunkten und blau entlang der ursprünglichen Kanten färbt, gibt es 8 Formen, 7 die sich topologisch unterscheiden. (Die abgeschnittene dreieckige Kachelung ist topologisch identisch mit der hexagonalen Kachelung.)

Gleichmäßige sechseckige/dreieckige Fliesen
Fundamentale Domänen	Symmetrie : [6,3], (*632)							[6,3] ⁺ , (632)
	{6,3}	t{6,3}	r{6,3}	t{3,6}	{3,6}	rr{6,3}	tr{6,3}	sr{6,3}


Konfig.	6 ³	3.12.12	(6.3) ²	6.6.6	3 ⁶	3.4.6.4	4.6.12	3.3.3.3.6

Monoedrische konvexe hexagonale Fliesen

Es gibt 3 Arten von monoedrischen konvexen hexagonalen Kacheln. Sie sind alle isoedrisch . Jeder hat parametrische Variationen innerhalb einer festen Symmetrie. Typ 2 enthält Gleitspiegelung und 2-isohedral keeping chiral Paare verschieden sind .

3 Arten von monoedrischen konvexen hexagonalen Fliesen
1	2		3
p2, 2222	pgg, 22×	p2, 2222	p3, 333

b=e B+C+D=360°	b=e, d=f B+C+E=360°		a=f, b=c, d=e B=D=F=120°
2-Fliesen-Gitter	4-Fliesen-Gitter		3-Fliesen-Gitter

Topologisch äquivalente Kacheln

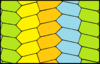
Hexagonale Kacheln können mit der identischen {6,3}-Topologie wie die reguläre Kachelung (3 Hexagone um jeden Scheitelpunkt) erstellt werden. Bei isohedralen Flächen gibt es 13 Variationen. Die angegebene Symmetrie setzt voraus, dass alle Gesichter die gleiche Farbe haben. Farben repräsentieren hier die Gitterpositionen. Einfarbige (1-Kachel) Gitter sind Parallelogon- Sechsecke.

13 isohedrisch gekachelte Sechsecke
Seite (××)	S.3 (333)	pmg (22*)

Seite (22×)	p31m (3*3)	p2 (2222)	cmm (2*22)	p6m (*632)

Andere isohedral gekachelte topologische hexagonale Kacheln werden als Vierecke und Fünfecke angesehen, die nicht Kante an Kante sind, sondern als kolineare benachbarte Kanten interpretiert:

Isoederförmig gekachelte Vierecke
pmg (22*)		Seite (22×)			cmm (2*22)	p2 (2222)
Parallelogramm	Trapezoid	Parallelogramm	Rechteck	Parallelogramm	Rechteck	Rechteck

Isoederförmig gekachelte Fünfecke
p2 (2222)	Seite (22×)	S.3 (333)

Die 2-einheitlichen und 3-einheitlichen Tessellationen haben einen Rotationsfreiheitsgrad, der 2/3 der Sechsecke verzerrt, einschließlich eines kolinearen Falls, der auch als eine nicht-randlose Kachelung von Sechsecken und größeren Dreiecken angesehen werden kann.

Es kann auch in ein chirales vierfarbiges tridirektionales Webmuster verzerrt werden, wodurch einige Sechsecke zu Parallelogrammen verzerrt werden . Das gewebte Muster mit 2 farbigen Gesichtern hat 632 (p6) Rotationssymmetrie . Ein Chevron- Muster hat eine pmg (22*)-Symmetrie, die mit 3 oder 4 farbigen Kacheln auf p1 (°) abgesenkt wird.

Regulär	Gyrated	Regulär	Gewebt	Chevron
p6m, (*632)	S.6, (632)	p6m (*632)	S.6 (632)	p1 (°)

p3m1, (*333)	p3, (333)	p6m (*632)	p2 (2222)	p1 (°)

Kreisverpackung

Die hexagonalen Kacheln können eingesetzt werden Kreis Verpackung , in der Mitte von jedem Punkt gleiche Durchmesser Kreise platzieren. Jeder Kreis hat Kontakt zu 3 anderen Kreisen in der Verpackung ( Kussnummer ). Die Lücke innerhalb jedes Sechsecks lässt einen Kreis zu, wodurch die dichteste Packung aus der dreieckigen Kachelung entsteht , wobei jeder Kreis maximal 6 Kreise berührt.

Siehe auch

Verweise

Coxeter, HSM Regular Polytopes , (3. Auflage, 1973), Dover-Ausgabe, ISBN 0-486-61480-8 p. 296, Tabelle II: Normale Waben
Grünbaum, Branko ; Shephard, GC (1987). Fliesen und Muster . New York: WH Freeman. ISBN 0-7167-1193-1.(Kapitel 2.1: Regelmäßige und einheitliche Fliesen , S. 58–65)
Williams, Robert (1979). Die geometrische Grundlage der natürlichen Struktur: Ein Quellbuch des Designs . Dover Publications, Inc. p. 35. ISBN 0-486-23729-X.
John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss , The Symmetries of Things 2008, ISBN 978-1-56881-220-5 [1]

Externe Links

DNA | urlname=HexagonalGrid | title=Hexagonales Gitter}}
- Weisstein, Eric W. "Regelmäßige Tesselation" . MathWorld .
- Weisstein, Eric W. "Einheitliche Tesselation" . MathWorld .
Klitzing, Richard. "2D euklidische Kacheln o3o6x - hexat - O3" .

v T e Grundlegende konvexe regelmäßige und gleichmäßige Waben in den Dimensionen 2-9
Platz	Familie	${\tilde {A}}_{n-1}$	${\tilde {C}}_{n-1}$	${\tilde {B}}_{n-1}$	${\tilde {D}}_{n-1}$	${\tilde {G}}_{2}$ / / ${\tilde {F}}_{4}$ ${\tilde {E}}_{n-1}$
E ²	Gleichmäßige Fliesenverlegung	{3 ^[3] }	δ ₃	hδ ₃	qδ ₃	Sechseckig
E ³	Gleichmäßige konvexe Wabe	{3 ^[4] }	δ ₄	hδ ₄	qδ ₄
E ⁴	Uniform 4-Waben	{3 ^[5] }	δ ₅	hδ ₅	qδ ₅	24-zellige Wabe
E ⁵	Uniform 5-Waben	{3 ^[6] }	δ ₆	hδ ₆	qδ ₆
E ⁶	Uniform 6-Waben	{3 ^[7] }	δ ₇	hδ ₇	qδ ₇	2 ₂₂
E ⁷	Uniform 7-Waben	{3 ^[8] }	δ ₈	hδ ₈	qδ ₈	1 ₃₃ • 3 ₃₁
E ⁸	Uniform 8-Waben	{3 ^[9] }	δ ₉	hδ ₉	qδ ₉	1 ₅₂ • 2 ₅₁ • 5 ₂₁
E ⁹	Uniform 9-Waben	{3 ^[10] }	δ ₁₀	hδ ₁₀	qδ ₁₀
E ¹⁰	Uniform 10-Waben	{3 ^[11] }	δ ₁₁	hδ ₁₁	qδ ₁₁
E ^{n -1}	Einheitlich ( n -1) - Wabe	{3 ^[n] }	δ _nein	hδ _n	qδ _n	1 _k2 • 2 _k1 • k ₂₁

Languages

In other projects