Ikosaeder - Icosahedron

In Geometrie , ein Ikosaeder ( / ˌ aɪ k ɒ s ə h í d r ən , - k ə -, - k oʊ - / oder / aɪ ˌ k ɒ s ə h í d r ən / ) ein Polyeder mit 20 Gesichter. Der Name kommt aus dem Altgriechischen εἴκοσι (eíkosi) „zwanzig“ und aus dem Altgriechischen ἕδρα (hédra) „Sitz“. Der Plural kann entweder "Ikosaeder" ( /- d r ə / ) oder "Ikosaeder" sein.

Es gibt unendlich viele nicht ähnliche Formen von Ikosaedern, von denen einige symmetrischer sind als andere. Am bekanntesten ist das ( konvexe , nicht sternförmige ) regelmäßige Ikosaeder – einer der platonischen Körper – dessen Flächen 20 gleichseitige Dreiecke sind .

Regelmäßige Ikosaeder

Zwei Arten von regelmäßigen Ikosaedern
Konvexes regelmäßiges Ikosaeder	Großes Ikosaeder

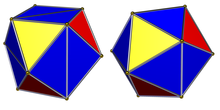
Es gibt zwei Objekte, ein konvexes und ein nichtkonvexes, die beide als reguläre Ikosaeder bezeichnet werden können. Jeder hat 30 Kanten und 20 gleichseitige Dreiecksflächen, wobei sich fünf an jedem seiner zwölf Eckpunkte treffen. Beide haben ikosaedrische Symmetrie . Der Begriff "reguläres Ikosaeder" bezieht sich im Allgemeinen auf die konvexe Variante, während die nichtkonvexe Form als großes Ikosaeder bezeichnet wird .

Konvexes regelmäßiges Ikosaeder

Das konvexe regelmäßige Ikosaeder wird normalerweise einfach als das regelmäßige Ikosaeder bezeichnet , einer der fünf regelmäßigen platonischen Körper , und wird durch sein Schläfli-Symbol {3, 5} dargestellt, das 20 Dreiecksflächen enthält, wobei sich 5 Flächen um jeden Scheitelpunkt treffen.

Sein duales Polyeder ist das regelmäßige Dodekaeder {5, 3} mit drei regelmäßigen fünfeckigen Flächen um jeden Scheitelpunkt.

Großes Ikosaeder

Der große Ikosaeder ist einer der vier regulären Kepler-Poinsot-Polyeder . Sein Schläfli-Symbol ist {3,5/2}. Wie die konvexe Form hat es auch 20 gleichseitige Dreiecksflächen, aber seine Scheitelfigur ist eher ein Pentagramm als ein Fünfeck, was zu geometrisch sich schneidenden Flächen führt. Die Schnittpunkte der Dreiecke stellen keine neuen Kanten dar.

Sein duales Polyeder ist das große sternförmige Dodekaeder {5/2, 3}, mit drei regelmäßigen fünfeckigen Sternflächen um jeden Scheitelpunkt herum.

Sternförmige Ikosaeder

Stellation ist der Vorgang, bei dem die Flächen oder Kanten eines Polyeders verlängert werden, bis sie sich zu einem neuen Polyeder treffen. Dies geschieht symmetrisch, so dass die resultierende Figur die Gesamtsymmetrie der Elternfigur beibehält.

In ihrem Buch The Fifty-Nine Icosahedra , Coxeter et al. zählte 58 solcher Stellationen des regelmäßigen Ikosaeders auf.

Von diesen haben viele ein einzelnes Gesicht in jeder der 20 Gesichtsebenen und sind daher auch Ikosaeder. Das große Ikosaeder gehört dazu.

Andere Sternbilder haben mehr als eine Fläche in jeder Ebene oder bilden Verbindungen einfacherer Polyeder. Diese sind nicht streng Ikosaeder, obwohl sie oft als solche bezeichnet werden.

(konvexes) Ikosaeder	Kleines triambisches Ikosaeder	Verbindung von fünf Oktaedern	Großes Ikosaeder	Ausgegrabener Dodekaeder
Bemerkenswerte Stellationen des Ikosaeders
Regulär	Einheitliche Duals	Regelmäßige Verbindungen	Normaler Stern	Andere


Der Stellationsprozess auf dem Ikosaeder erzeugt eine Reihe verwandter Polyeder und Verbindungen mit Ikosaedersymmetrie .

Pyritoedrische Symmetrie

Pyritoedrische und tetraedrische Symmetrien

Coxeter-Diagramme

(pyritoedrisch)

(tetraedrisch)

Schläfli-Symbol

s{3,4}
sr{3,3} oder

s{\begin{Bmatrix}3\\3\end{Bmatrix}}

Gesichter

20 Dreiecke:
8 gleichseitige
12 gleichschenklige

Kanten

30 (6 kurz + 24 lang)

Scheitelpunkte

12

Symmetriegruppe

T _h , [4,3 ⁺ ], (3*2), Ordnung 24

Rotationsgruppe

T _d , [3,3] ⁺ , (332), Ordnung 12

Doppelpolyeder

Pyritoeder

Eigenschaften

konvex

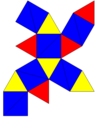
Netz


Ein regelmäßiges Ikosaeder ist topologisch identisch mit einem Kuboktaeder mit seinen 6 quadratischen Flächen, die auf Diagonalen mit Pyritoeder-Symmetrie halbiert sind.

Ein Ikosaeder kann als untere verzerrt oder markiert werden pyritohedral Symmetrie und ist ein sogenannter Einschnürtrommel Oktaeder , Einschnürtrommel tetratetrahedron , Einschnürtrommel Tetraeders und pseudo-Ikosaeder . Dies kann als alternierender abgeschnittener Oktaeder angesehen werden . Wenn alle Dreiecke gleichseitig sind , kann die Symmetrie auch dadurch unterschieden werden, dass die 8- und 12-Dreiecksätze unterschiedlich eingefärbt werden.

Pyritoedrische Symmetrie hat das Symbol (3*2), [3 ⁺ ,4], mit Ordnung 24. Tetraeder Symmetrie hat das Symbol (332), [3,3] ⁺ , mit Ordnung 12. Diese niedrigeren Symmetrien erlauben geometrische Verzerrungen ab 20 gleichseitige Dreiecksflächen, stattdessen mit 8 gleichseitigen Dreiecken und 12 kongruenten gleichschenkligen Dreiecken .

Diese Symmetrien bieten Coxeter-Diagramme : und jeweils die niedrigere Symmetrie zum regulären Ikosaeder darstellen , (*532), [5,3] ikosaedrische Symmetrie der Ordnung 120.

Kartesischen Koordinaten

Konstruktion aus den Eckpunkten eines abgeschnittenen Oktaeders , der innere Rechtecke zeigt.

Die Koordinaten der 12 Eckpunkte können durch die Vektoren definiert werden, die durch alle möglichen zyklischen Permutationen und Vorzeichenwechsel von Koordinaten der Form (2, 1, 0) definiert werden. Diese Koordinaten repräsentieren das abgeschnittene Oktaeder mit gelöschten abwechselnden Scheitelpunkten.

Diese Konstruktion ist ein sogenannter Einschnürtrommel Tetraeders in seiner Ikosaeder Form, durch die gleichen Operationen durchgeführt , erzeugte mit dem Vektor ausgehend ( φ , 1, 0), wobei φ die ist goldenes Verhältnis .

Jessens Ikosaeder

In Jessens Ikosaeder, manchmal auch Jessens orthogonaler Ikosaeder genannt , sind die 12 gleichschenkligen Flächen unterschiedlich angeordnet, so dass die Figur nicht konvex ist und rechtwinklige Diederwinkel hat .

Es ist eine zu einem Würfel kongruente Schere , was bedeutet, dass sie in kleinere polyedrische Stücke geschnitten werden kann, die neu angeordnet werden können, um einen festen Würfel zu bilden.

Andere Ikosaeder

Rhombischer Ikosaeder

Das rhombische Ikosaeder ist ein Zonoeder , der aus 20 kongruenten Rauten besteht. Es kann aus dem rhombischen Triacontaeder abgeleitet werden, indem 10 Mittelflächen entfernt werden. Obwohl alle Gesichter kongruent sind, ist das rhombische Ikosaeder nicht gesichtstransitiv .

Pyramiden- und Prismensymmetrien

Häufige Ikosaeder mit Pyramiden- und Prismensymmetrien sind:

19-seitige Pyramide (plus 1 Basis = 20).
18-seitiges Prisma (plus 2 Enden = 20).
9-seitiges Antiprisma (2 Sätze von 9 Seiten + 2 Enden = 20).
10-seitige Doppelpyramide (2 Sätze von 10 Seiten = 20).
10-seitiges Trapezoeder (2 Sätze von 10 Seiten = 20).

Johnson-Feststoffe

Mehrere Johnson-Feststoffe sind Ikosaeder:

J22	J35	J36	J59	J60	J92
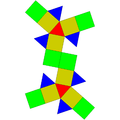
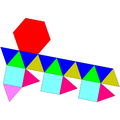
Kreiselgestreckte dreieckige Kuppel	Längliche dreieckige orthobicupola	Längliche dreieckige Gyrobicupola	Parabiaaugmentiertes Dodekaeder	Metabiaaugmentiertes Dodekaeder	Dreieckige Hebesphenorotunda

16 Dreiecke 3 Quadrate 1 Sechseck	8 Dreiecke 12 Quadrate	8 Dreiecke 12 Quadrate	10 Dreiecke 10 Fünfecke	10 Dreiecke 10 Fünfecke	13 Dreiecke 3 Quadrate 3 Fünfecke 1 Sechseck