Mikrokanonisches Ensemble - Microcanonical ensemble

Statistische Mechanik
Thermodynamik Kinetische Theorie
Partikelstatistik Spin-Statistik-Theorem Identische Partikel Maxwell–Boltzmann Bose–Einstein Fermi-Dirac Parastatistik Anyonic-Statistiken Geflechtstatistiken
Thermodynamische Ensembles NVE Microcanonical NVT Canonical μVT großkanonische NPH Isoenthalp–isobar NPT Isotherm–isobar
Modelle Debye Einstein Ich singe Potts
Potenziale Innere Energie Enthalpie Freie Helmholtz-Energie Gibbs freie Energie Großes Potenzial / Freie Energie Landau
Wissenschaftler Maxwell Boltzmann Gibbs Einstein Ehrenfest von Neumann Tolman Debye Fermi Bose
v T e

In der statistischen Mechanik ist das mikrokanonische Ensemble ein statistisches Ensemble , das die möglichen Zustände eines mechanischen Systems darstellt, dessen Gesamtenergie genau angegeben ist. Das System wird in dem Sinne als isoliert angenommen, dass es keine Energie oder Teilchen mit seiner Umgebung austauschen kann, so dass sich (durch Energieerhaltung ) die Energie des Systems mit der Zeit nicht ändert.

Die primären makroskopischen Variablen des mikrokanonischen Ensembles sind die Gesamtzahl der Teilchen im System (Symbol: N ), das Volumen des Systems (Symbol: V ) sowie die Gesamtenergie im System (Symbol: E ). Jede davon wird im Ensemble als konstant angenommen. Aus diesem Grund wird das mikrokanonische Ensemble manchmal als NVE- Ensemble bezeichnet .

Einfach ausgedrückt, wird das mikrokanonische Ensemble definiert, indem jedem Mikrozustand, dessen Energie in einen bei E zentrierten Bereich fällt , eine gleiche Wahrscheinlichkeit zugewiesen wird . Alle anderen Mikrozustände erhalten eine Wahrscheinlichkeit von Null. Da sich die Wahrscheinlichkeiten zu 1 addieren müssen, ist die Wahrscheinlichkeit P der Kehrwert der Anzahl der Mikrozustände W im Energiebereich,

${\displaystyle P=1/W,}$

Der Energiebereich wird dann in der Breite reduziert, bis er unendlich schmal ist und immer noch bei E zentriert ist . Im Grenzbereich dieses Prozesses wird das mikrokanonische Ensemble erhalten.

Anwendbarkeit

Aufgrund seiner Verbindung mit den elementaren Annahmen der statistischen Gleichgewichtsmechanik (insbesondere dem Postulat a priori gleicher Wahrscheinlichkeiten ) ist die mikrokanonische Gesamtheit ein wichtiger konzeptioneller Baustein der Theorie. Sie wird manchmal als die grundlegende Verteilung der statistischen Gleichgewichtsmechanik angesehen. Es ist auch in einigen numerischen Anwendungen nützlich, wie z. B. in der Molekulardynamik . Andererseits sind die meisten nichttrivialen Systeme im mikrokanonischen Ensemble mathematisch schwer zu beschreiben, und es gibt auch Unklarheiten bezüglich der Definitionen von Entropie und Temperatur. Aus diesen Gründen werden für theoretische Berechnungen oft andere Ensembles bevorzugt.

Die Anwendbarkeit des mikrokanonischen Ensembles auf reale Systeme hängt von der Bedeutung von Energiefluktuationen ab, die aus Wechselwirkungen zwischen dem System und seiner Umgebung sowie unkontrollierten Faktoren bei der Vorbereitung des Systems resultieren können. Im Allgemeinen sind Schwankungen vernachlässigbar, wenn ein System makroskopisch groß ist oder wenn es mit genau bekannter Energie hergestellt und danach von seiner Umgebung nahezu isoliert gehalten wird. In solchen Fällen ist das mikrokanonische Ensemble anwendbar. Ansonsten sind andere Ensembles besser geeignet – wie das kanonische Ensemble (Schwankende Energie) oder das großkanonische Ensemble (Schwankende Energie und Teilchenzahl).

Eigenschaften

Thermodynamische Größen

Das grundlegende thermodynamische Potenzial des mikrokanonischen Ensembles ist die Entropie . Es gibt mindestens drei mögliche Definitionen, die jeweils durch die Phasenvolumenfunktion v ( E ) angegeben werden , die die Gesamtzahl der Zustände mit einer Energie kleiner als E zählt (siehe den Abschnitt Präzise Ausdrücke für die mathematische Definition von v ):

Im mikrokanonischen Ensemble ist die Temperatur eine abgeleitete Größe und kein externer Kontrollparameter. Sie ist definiert als die Ableitung der gewählten Entropie nach der Energie. Beispielsweise kann man die „Temperaturen“ T _v und T _s wie folgt definieren:

${\displaystyle 1/T_{v}=dS_{v}/dE,}$

${\displaystyle 1/T_{s}=dS_{s}/dE=dS_{\text{B}}/dE.}$

Wie die Entropie gibt es mehrere Möglichkeiten, die Temperatur im mikrokanonischen Ensemble zu verstehen. Allgemeiner gesagt ist die Übereinstimmung zwischen diesen ensemblebasierten Definitionen und ihren thermodynamischen Gegenstücken nicht perfekt, insbesondere für endliche Systeme.

Der mikrokanonische Druck und das chemische Potential sind gegeben durch:

${\displaystyle {\frac {p}{T}}={\frac {\partial S}{\partial V}};\qquad {\frac {\mu}{T}}=-{\frac {\partial S}{\partielles N}}}$

Phasenübergänge

Nach ihrer strengen Definition entsprechen Phasenübergänge dem nichtanalytischen Verhalten im thermodynamischen Potential oder seinen Ableitungen. Nach dieser Definition können Phasenübergänge im mikrokanonischen Ensemble in Systemen beliebiger Größe auftreten. Dies steht im Gegensatz zu den kanonischen und großkanonischen Ensembles, bei denen Phasenübergänge nur im thermodynamischen Limes auftreten können , also in Systemen mit unendlich vielen Freiheitsgraden. Grob gesagt führen die Reservoirs, die die kanonischen oder großkanonischen Ensembles definieren, Fluktuationen ein, die jedes nichtanalytische Verhalten in der freien Energie endlicher Systeme "glätten". Dieser Glättungseffekt ist in makroskopischen Systemen normalerweise vernachlässigbar, da diese so groß sind, dass die freie Energie dem nichtanalytischen Verhalten sehr gut angenähert werden kann. Der technische Unterschied bei Ensembles kann jedoch bei der theoretischen Analyse kleiner Systeme von Bedeutung sein.

Informationsentropie

Für ein gegebenes mechanisches System (festes N , V ) und einen gegebenen Energiebereich maximiert die gleichmäßige Verteilung der Wahrscheinlichkeit über Mikrozustände (wie in der mikrokanonischen Gesamtheit) den Gesamtmittelwert −⟨log P ⟩ .

Thermodynamische Analogien

Frühe Arbeiten in der statistischen Mechanik von Ludwig Boltzmann führten zu seiner gleichnamigen Entropiegleichung für ein System einer gegebenen Gesamtenergie, S = k log W , wobei W die Anzahl der verschiedenen Zustände ist, die dem System bei dieser Energie zugänglich sind. Boltzmann ging nicht weiter darauf ein, was genau die Menge der verschiedenen Zustände eines Systems ausmacht, abgesehen vom Spezialfall eines idealen Gases. Dieses Thema wurde von Josiah Willard Gibbs vollständig untersucht , der die verallgemeinerte statistische Mechanik für beliebige mechanische Systeme entwickelt und das in diesem Artikel beschriebene mikrokanonische Ensemble definiert hat. Gibbs untersuchte sorgfältig die Analogien zwischen der mikrokanonischen Gesamtheit und der Thermodynamik, insbesondere wie sie sich bei Systemen mit wenigen Freiheitsgraden auflösen. Er führte zwei weitere Definitionen der mikrokanonischen Entropie ein, die nicht von ω - der oben beschriebenen Volumen- und Oberflächenentropie - abhängen . (Beachten Sie, dass sich die Oberflächenentropie von der Boltzmann-Entropie nur durch einen ω -abhängigen Offset unterscheidet.)

Die Volumenentropie S _v und die zugehörige T _v bilden eine enge Analogie zur thermodynamischen Entropie und Temperatur. Genau das kann man zeigen

${\displaystyle dE=T_{\rm {v}}dS_{\rm {v}}-\langle P\rangle dV,}$

( ⟨ P ⟩ ist der durchschnittliche Gesamtdruck) wie für den ersten Hauptsatz der Thermodynamik erwartet . Eine ähnliche Gleichung kann für die Oberflächenentropie (Boltzmann) und die zugehörige T _{s gefunden werden} , jedoch ist der "Druck" in dieser Gleichung eine komplizierte Größe, die nichts mit dem mittleren Druck zu tun hat.

Die mikrokanonischen T _v und T _s sind in ihrer Analogie zur Temperatur nicht ganz zufriedenstellend. Außerhalb der thermodynamischen Grenze treten eine Reihe von Artefakten auf.

• Nicht triviales Ergebnis der Kombination zweier Systeme : Zwei Systeme, die jeweils durch ein unabhängiges mikrokanonisches Ensemble beschrieben werden, können in thermischen Kontakt gebracht und zu einem kombinierten System, das auch durch ein mikrokanonisches Ensemble beschrieben wird, ausgleichen. Leider kann der Energiefluss zwischen den beiden Systemen nicht basierend auf den anfänglichen Ts vorhergesagt werden . Selbst wenn die anfänglichen T gleich sind, kann Energie übertragen werden. Außerdem unterscheidet sich das T der Kombination von den Anfangswerten. Dies widerspricht der Intuition, dass die Temperatur eine intensive Größe sein sollte und dass zwei temperaturgleiche Systeme nicht durch thermischen Kontakt beeinflusst werden sollten.
• Seltsames Verhalten für Systeme mit wenigen Teilchen : Viele Ergebnisse wie das mikrokanonische Äquipartitionstheorem erhalten einen Offset von ein oder zwei Freiheitsgraden, wenn sie in Form von T _{s geschrieben werden} . Für kleine Systeme ist dieser Offset signifikant, und wenn wir also S _s zum Analogon der Entropie machen, müssen für Systeme mit nur einem oder zwei Freiheitsgraden mehrere Ausnahmen gemacht werden.
• Falsche negative Temperaturen : Ein negatives T _s tritt immer dann auf, wenn die Zustandsdichte mit der Energie abnimmt. In einigen Systemen ist die Zustandsdichte energetisch nicht monoton , und so kann T _s mit zunehmender Energie das Vorzeichen mehrfach ändern.

Die bevorzugte Lösung für diese Probleme besteht darin, die Verwendung des mikrokanonischen Ensembles zu vermeiden. In vielen realistischen Fällen wird ein System auf ein Wärmebad thermostatisiert, so dass die Energie nicht genau bekannt ist. Eine genauere Beschreibung ist dann das kanonische Ensemble oder das großkanonische Ensemble , die beide vollständig der Thermodynamik entsprechen.

Präzise Ausdrücke für das Ensemble

Der genaue mathematische Ausdruck für ein statistisches Ensemble hängt von der Art der betrachteten Mechanik ab – Quanten- oder klassische Mechanik –, da sich der Begriff „Mikrozustand“ in diesen beiden Fällen erheblich unterscheidet. In der Quantenmechanik liefert die Diagonalisierung einen diskreten Satz von Mikrozuständen mit spezifischen Energien. Der klassische mechanische Fall beinhaltet stattdessen ein Integral über den kanonischen Phasenraum , und die Größe der Mikrozustände im Phasenraum kann etwas willkürlich gewählt werden.

Um das mikrokanonische Ensemble zu konstruieren, ist es in beiden Mechaniken erforderlich, zunächst einen Energiebereich anzugeben. In der Ausdrücken unter der Funktion (eine Funktion von H , bei Peaking E mit einer Breite ω ) verwendet werden , um den Bereich der Energie darzustellen , in dem Zustand einschließen. Ein Beispiel für diese Funktion wäre ${\displaystyle f({\tfrac {HE}{\omega }})}$

${\displaystyle f(x)={\begin{cases}1,&\mathrm {if} ~|x|<{\tfrac {1}{2}},\\0,&\mathrm {sonst.} \ Ende{Fälle}}}$

oder, einfacher,

${\displaystyle f(x)=e^{-\pi x^{2}}.}$

Quantenmechanik

Beispiel eines mikrokanonischen Ensembles für ein Quantensystem bestehend aus einem Teilchen in einem Potentialtopf.

Darstellung aller möglichen Zustände dieses Systems. Die verfügbaren stationären Zustände werden als horizontale Balken unterschiedlicher Dunkelheit gemäß | . angezeigt ψ _i (x) | ² .

Ein Ensemble, das nur die Zustände innerhalb eines engen Energieintervalls enthält. Wenn die Energiebreite auf Null gesetzt wird, wird ein mikrokanonisches Ensemble erhalten (vorausgesetzt, das Intervall enthält mindestens einen Zustand).

Der Hamilton-Operator des Teilchens ist vom Schrödinger- Typ, Ĥ = U ( x ) + p ² /2 m (das Potential U ( x ) ist als rote Kurve aufgetragen). Jedes Feld zeigt ein Energiepositionsdiagramm mit den verschiedenen stationären Zuständen zusammen mit einem Seitendiagramm, das die Verteilung der Energiezustände zeigt.

Ein statistisches Ensemble in der Quantenmechanik wird durch eine Dichtematrix repräsentiert , die mit bezeichnet wird . Die mikrokanonische Gesamtheit kann in der Bra-Ket-Notation in Form der Energieeigenzustände und Energieeigenwerte des Systems geschrieben werden . Gegeben eine vollständige Basis von Energieeigenzuständen | ψ _i ⟩ , indexiert durch i , die mikrokanonische Gesamtheit ist ${\displaystyle {\hat {\rho}}}$

${\displaystyle {\hat{\rho}}={\frac {1}{W}}\sum _{i}f\left({\tfrac {H_{i}-E}{\omega}}\right )|\psi_{i}\rangle\langle\psi_{i}|,}$

wobei die H _i die Energieeigenwerte sind, die durch bestimmt werden (hier ist Ĥ der Gesamtenergieoperator des Systems, dh der Hamilton-Operator ). Der Wert von W wird bestimmt, indem verlangt wird, dass es sich um eine normalisierte Dichtematrix handelt, und so ${\displaystyle {\hat{H}}|\psi_{i}\rangle =H_{i}|\psi_{i}\rangle}$${\displaystyle {\hat {\rho}}}$

${\displaystyle W=\sum_{i}f\left({\tfrac {H_{i}-E}{\omega}}\right).}$

Die Zustandsvolumenfunktion (zur Berechnung der Entropie) ist gegeben durch

${\displaystyle v(E)=\sum _{H_{i}<E}1.}$

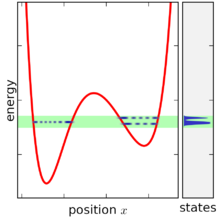
Das mikrokanonische Ensemble wird definiert, indem die Grenze der Dichtematrix genommen wird, wenn die Energiebreite auf Null geht, jedoch tritt eine problematische Situation auf, sobald die Energiebreite kleiner wird als der Abstand zwischen den Energieniveaus. Bei sehr kleiner Energiebreite existiert das Ensemble für die meisten Werte von E überhaupt nicht , da keine Zustände in den Bereich fallen. Wenn das Ensemble existiert, enthält es normalerweise nur einen ( oder zwei ) Zustände, da in einem komplexen System die Energieniveaus nur zufällig immer gleich sind (siehe die Zufallsmatrixtheorie für weitere Diskussionen zu diesem Punkt). Außerdem nimmt die Zustands-Volumen-Funktion auch nur in diskreten Inkrementen zu, sodass ihre Ableitung immer nur unendlich oder null ist, was die Definition der Zustandsdichte erschwert. Dieses Problem lässt sich dadurch lösen, dass man den Energiebereich nicht vollständig auf Null setzt und die Zustandsvolumenfunktion glättet, was jedoch die Definition des Ensembles komplizierter macht, da es dann notwendig wird, den Energiebereich neben anderen Variablen (zusammen , ein NVEω- Ensemble).

Klassische Mechanik

Beispiel für ein mikrokanonisches Ensemble für ein klassisches System bestehend aus einem Teilchen in einem Potentialtopf.

Darstellung aller möglichen Zustände dieses Systems. Die verfügbaren physikalischen Zustände sind im Phasenraum gleichmäßig verteilt, jedoch mit einer ungleichmäßigen Energieverteilung; das Seitendiagramm zeigt dv / dE an .

Ein Ensemble, das nur auf die Zustände innerhalb eines engen Energieintervalls beschränkt ist. Dieses Ensemble erscheint als dünne Schale im Phasenraum. Wenn die Energiebreite auf Null gebracht wird, wird ein mikrokanonisches Ensemble erhalten.

Jedes Panel zeigt den Phasenraum (obere Grafik) und den Energiepositionsraum (untere Grafik). Der Hamiltonoperator des Teilchens ist H = U ( x ) + p ² /2 m , wobei das Potential U ( x ) als rote Kurve dargestellt ist. Das Seitendiagramm zeigt die Verteilung der Zustände in der Energie.

In der klassischen Mechanik wird ein Ensemble durch eine über den Phasenraum des Systems definierte gemeinsame Wahrscheinlichkeitsdichtefunktion ρ ( p ₁ , … p _n , q ₁ , … q _n ) dargestellt . Der Phasenraum hat n verallgemeinerte Koordinaten namens q ₁ , … q _n und n zugehörige kanonische Impulse namens p ₁ , … p _n .

Die Wahrscheinlichkeitsdichtefunktion für die mikrokanonische Gesamtheit lautet:

${\displaystyle \rho ={\frac {1}{h^{n}C}}{\frac {1}{W}}f({\tfrac {HE}{\omega}}),}$

wo

• H ist die Gesamtenergie ( Hamiltonian ) des Systems, eine Funktion der Phase ( p ₁ , … q _n ) ,
• h ist eine willkürlicheaber vorbestimmte Konstante mit den Einheiten der Energie x Zeit ,das Ausmaß eines Mikrozustand einstellen und korrekte Abmessungen bereitzustellen ρ .
• C ist ein Überzähl-Korrekturfaktor, der häufig für Partikelsysteme verwendet wird, in denen identische Partikel ihren Platz untereinander tauschen können.

Auch hier wird der Wert von W bestimmt, indem verlangt wird, dass ρ eine normalisierte Wahrscheinlichkeitsdichtefunktion ist:

${\displaystyle W=\int\ldots\int {\frac {1}{h^{n}C}}f({\tfrac {HE}{\omega}})\,dp_{1}\ldots dq_{ n}}$

Dieses Integral wird über den gesamten Phasenraum genommen . Die Zustandsvolumenfunktion (zur Berechnung der Entropie) ist definiert durch

${\displaystyle v(E)=\int\ldots\int_{H<E}{\frac{1}{h^{n}C}}\,dp_{1}\ldots dq_{n}.}$

Da die Energiebreite ω auf Null genommen wird, der Wert von W sinkt proportional zu & ohgr; als W = ω ( dv / dE ) .

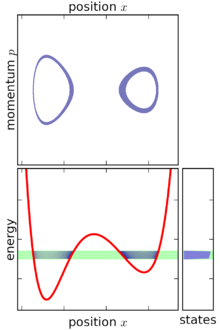
Basierend auf der obigen Definition kann das mikrokanonische Ensemble als eine infinitesimal dünne Schale im Phasenraum visualisiert werden, die auf einer konstanten Energiefläche zentriert ist. Obwohl das mikrokanonische Ensemble auf diese Oberfläche beschränkt ist, ist es nicht unbedingt gleichmäßig über diese Oberfläche verteilt: Wenn der Energiegradient im Phasenraum variiert, dann ist das mikrokanonische Ensemble in einigen Teilen der Oberfläche „dicker“ (konzentrierter) als in anderen . Dieses Merkmal ist eine unvermeidliche Folge der Forderung, dass das mikrokanonische Ensemble ein stationäres Ensemble ist.

Beispiele

Ideales Gas

Die Grundgröße in der mikrokanonischen Gesamtheit ist , die gleich dem mit gegebenem Phasenraumvolumen ist . Aus können alle thermodynamischen Größen berechnet werden. Bei einem idealen Gas ist die Energie unabhängig von den Teilchenpositionen, die daher einen Faktor von zu tragen . Die Impulse hingegen sind auf eine -dimensionale (hyper-)sphärische Schale mit Radius beschränkt ; ihr Beitrag ist gleich dem Oberflächenvolumen dieser Schale. Der resultierende Ausdruck für ist: ${\displaystyle W(E,V,N)}$${\displaystyle (E,V,N)}$${\displaystyle W}$${\displaystyle V^{N}}$${\displaystyle W}$${\displaystyle 3N}$${\displaystyle {\sqrt {2mE}}}$${\displaystyle W}$

${\displaystyle W={\frac {V^{N}}{N!}}{\frac {2\pi^{3N/2}}{\Gamma (3N/2)}}\left(2mE\right )^{(3N-1)/2}}$

wo ist die Gamma-Funktion , und der Faktor wurde aufgenommen, um die Ununterscheidbarkeit von Partikeln zu berücksichtigen (siehe Gibbs-Paradox ). In der großen Grenze, die Boltzmann - Entropie ist ${\displaystyle \Gamma (.)}$${\displaystyle N!}$${\displaystyle N}$${\displaystyle S=k_{\textrm {B}}\log W}$

${\displaystyle S=k_{\rm {B}}N\log \left[{\frac {V}{N}}\left({\frac {4\pi m}{3}}{\frac {E }{N}}\right)^{3/2}\right]+{\frac {5}{2}}k_{\rm {B}}N+O\left(\log N\right)}$

Dies wird auch als Sackur-Tetrode-Gleichung bezeichnet .

Die Temperatur ist gegeben durch

${\displaystyle {\frac {1}{T}}\equiv {\frac {\partial S}{\partial E}}={\frac {3}{2}}{\frac {Nk_{\textrm {B } }}{E}}}$

was mit analogem Ergebnis aus der kinetischen Gastheorie übereinstimmt . Die Berechnung des Drucks ergibt das ideale Gasgesetz :

${\displaystyle {\frac {p}{T}}\equiv {\frac {\partial S}{\partial V}}={\frac {Nk_{\mathrm {B}}}{V}}\quad\ Pfeil nach rechts \quad pV=Nk_{\mathrm {B} }T}$

Schließlich ist das chemische Potential ist ${\displaystyle\mu}$

${\displaystyle \mu \equiv -T{\frac {\partial S}{\partial N}}=k_{\rm {B}}T\log \left[{\frac {V}{N}}\, \left({\frac {4\pi mE}{3N}}\right)^{3/2}\right]}$

Ideales Gas in einem gleichmäßigen Gravitationsfeld

Das mikrokanonische Phasenvolumen kann auch explizit für ein ideales Gas in einem gleichmäßigen Gravitationsfeld berechnet werden .

Die Ergebnisse werden im Folgenden für ein dreidimensionales ideales Gas aus Partikeln mit jeweils einer Masse angegeben , die in einem thermisch isolierten Behälter eingeschlossen sind, der in z- Richtung unendlich lang ist und eine konstante Querschnittsfläche hat . Es wird angenommen, dass das Gravitationsfeld in der Minus- z- Richtung mit Stärke wirkt . Das Phasenvolumen ist ${\displaystyle N}$${\displaystyle m}$${\displaystyle A}$${\displaystyle g}$${\displaystyle W(E,N)}$

${\displaystyle W(E,N)={\frac {(2\pi)^{3N/2}A^{N}m^{N/2}}{g^{N}\Gamma (5N/2 )}}E^{{\frac {5N}{2}}-1}}$

wo ist die Gesamtenergie, kinetisch plus Gravitation. ${\displaystyle E}$

Die Gasdichte als Funktion der Höhe kann durch Integration über die Phasenvolumenkoordinaten erhalten werden. Das Ergebnis ist: ${\displaystyle \rho (z)}$${\displaystyle z}$

${\displaystyle \rho(z)=\left({\frac{5N}{2}}-1\right){\frac {mg}{E}}\left(1-{\frac {mgz}{E }}\right)^{{\frac {5N}{2}}-2}}$

Ebenso ist die Verteilung der Geschwindigkeitsgröße (gemittelt über alle Höhen) ${\displaystyle |{\vec {v}}|}$

${\displaystyle f(|{\vec {v}}|)={\frac {\Gamma (5N/2)}{\Gamma (3/2)\Gamma (5N/2-3/2)}}\ mal {\frac {m^{3/2}|{\vec {v}}|^{2}}{2^{1/2}E^{3/2}}}\times \left(1- {\frac {m|{\vec {v}}|^{2}}{2E}}\right)^{\frac {5(N-1)}{2}}}$

Die Analoga dieser Gleichungen im kanonischen Ensemble sind die barometrische Formel bzw. die Maxwell-Boltzmann-Verteilung . In der Grenze fallen der mikrokanonische und der kanonische Ausdruck zusammen; sie unterscheiden sich jedoch für endliche . Insbesondere im mikrokanonischen Ensemble sind die Positionen und Geschwindigkeiten statistisch nicht unabhängig. Als Ergebnis ist die kinetische Temperatur, definiert als die durchschnittliche kinetische Energie in einem gegebenen Volumen , im gesamten Behälter ungleichmäßig: ${\displaystyle N\rightarrow\infty}$${\displaystyle N}$${\displaystyle A\,dz}$

${\displaystyle T_{\mathrm {kinetisch}}={\frac {3E}{5N-2}}\left(1-{\frac {mgz}{E}}\right)}$

Im Gegensatz dazu ist die Temperatur im kanonischen Ensemble für alle einheitlich . ${\displaystyle N}$

Siehe auch

• Isoliertes System
• Ergodische Hypothese
• Loschmidts Paradoxon

Anmerkungen

Verweise