Vektorpaket - Vector bundle

Der (unendlich ausgedehnte) Möbiusstreifen ist ein Linienbündel über der 1-Kugel S ¹ . Lokal um jeden Punkt in S ¹ , es sieht aus wie U × R (wobei U eine offene Bogen einschließlich dem Punkt ist), aber die Gesamtbündel unterscheidet sich von S ¹ × R (das ist ein Zylinder statt).

In der Mathematik ist ein Vektorbündel eine topologische Konstruktion, die die Idee einer Familie von Vektorräumen präzisiert, die durch einen anderen Raum X parametrisiert sind (z. B. könnte X ein topologischer Raum , eine Mannigfaltigkeit oder eine algebraische Varietät sein ): zu jedem Punkt x von dem Raum X assoziieren (oder "anhängen") wir einen Vektorraum V ( x ) so, dass diese Vektorräume zusammenpassen, um einen anderen Raum der gleichen Art wie X zu bilden (zB ein topologischer Raum, Mannigfaltigkeit oder algebraische Varietät) , das dann als Vektorbündel über X bezeichnet wird .

Das einfachste Beispiel ist der Fall , dass die Familie der Vektorräume konstant ist, dh es gibt eine feste Vektorraum V , so dass V ( x ) = V für alle x in X : in diesem Fall gibt es eine Kopie von V für jedes x in X und diese Kopien passen zusammen, um das Vektorbündel X × V über X zu bilden . Solche Vektorbündel nennt man trivial . Eine kompliziertere (und prototypische) -Klasse der Beispiele sind die Tangentialbündel von glatten (oder differenzierbar) Verteilern : zu jedem Punkt dieser einen Verteiler befestigen wir den Tangentenraum mit dem Verteiler an diesem Punkt. Tangentialbündel sind im Allgemeinen keine trivialen Bündel. Zum Beispiel ist das Tangentenbündel der Kugel nach dem Hairy-Ball-Theorem nicht trivial . Im Allgemeinen heißt eine Mannigfaltigkeit genau dann parallelisierbar , wenn ihr Tangentenbündel trivial ist.

Vektorbündel müssen jedoch fast immer lokal trivial sein , dh sie sind Beispiele für Faserbündel . Außerdem müssen die Vektorräume normalerweise über den reellen oder komplexen Zahlen liegen, wobei in diesem Fall das Vektorbündel als reelles oder komplexes Vektorbündel bezeichnet wird. Komplexe Vektorbündel können als reelle Vektorbündel mit zusätzlicher Struktur betrachtet werden. Im Folgenden konzentrieren wir uns auf reelle Vektorbündel in der Kategorie der topologischen Räume .

Definition und erste Konsequenzen

Ein Vektorbündel über einer Basis . Ein Punkt in entspricht dem Ursprung in einer Faser des Vektorbündels , und diese Faser wird durch die Projektion auf den Punkt herab abgebildet .

E

M

m_{1}

M

E_{m_{1}}

E

m_{1}

\pi :E\to M

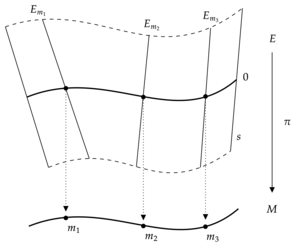
Ein reelles Vektorbündel besteht aus:

topologische Räume X ( Basisraum ) und E ( Gesamtraum )
eine stetige Surjektion $π$ : E → X ( Bündelprojektion )
für jedes x in X die Struktur eines endlichdimensionalen reellen Vektorraums auf der Faser $π$ ⁻¹ ({ x })

wobei folgende Kompatibilitätsbedingung erfüllt ist: Für jeden Punkt p in X gibt es eine offene Umgebung U ⊆ X von p , eine natürliche Zahl k und einen Homöomorphismus

{\displaystyle\varphi\colon U\times\mathbf{R}^{k}\to\pi^{-1}(U)}

so dass für alle x ∈ U ,

$(\pi\circ\varphi)(x,v)=x$ für alle Vektoren v in R ^k , und
die Abbildung ist ein linearer Isomorphismus zwischen den Vektorräumen R ^k und $π$ ⁻¹ ({ x }). $v\mapsto\varphi (x,v)$

Die offene Umgebung U zusammen mit dem Homöomorphismus wird als lokale Trivialisierung des Vektorbündels bezeichnet. Die lokale Trivialisierung zeigt, dass die Karte $π$ lokal "wie" die Projektion von U × R ^k auf U "sieht" . ${\displaystyle\varphi}$

Jede Faser $π$ ⁻¹ ({ x }) ist ein endlichdimensionaler reeller Vektorraum und hat daher eine Dimension k _x . Die lokalen Trivialisierungen zeigen , dass die Funktion x ↦ k _x ist lokal konstant und ist daher konstant auf jeder verbundenen Komponente von X . Wenn k _x gleich einer Konstanten k auf ganz X ist , dann heißt k der Rang des Vektorbündels und E heißt ein Vektorbündel vom Rang k . Oft beinhaltet die Definition eines Vektorbündels, dass der Rang wohldefiniert ist, sodass k _x konstant ist. Vektorbündel vom Rang 1 werden als Linienbündel bezeichnet , während diejenigen vom Rang 2 seltener als ebene Bündel bezeichnet werden.

Das kartesische Produkt X × R ^k , ausgestattet mit der Projektion X × R ^k → X , heißt triviales Bündel vom Rang k über X .

Übergangsfunktionen

Zwei triviale Vektorbündel über offene Mengen und können durch Übergangsfunktionen über den Schnittpunkt geklebt werden, die dazu dienen, die grau schattierten Bereiche nach Anwendung einer linearen Transformation auf die Fasern zusammenzukleben (man beachte die Transformation des blauen Vierecks unter dem Effekt von ). Unterschiedliche Wahlen von Übergangsfunktionen können zu unterschiedlichen Vektorbündeln führen, die nach Abschluss des Klebens nicht trivial sind.

U_{\alpha}

U_{\beta}

U_{\alpha\beta}

g_{\alpha\beta}

g_{\alpha\beta}

Der Möbius-Streifen kann durch ein nicht-triviales Kleben zweier trivialer Bündel auf offene Teilmengen U und V des Kreises S ¹ konstruiert werden . Trivial verklebt (mit g _UV =1 ) erhält man das triviale Bündel, aber mit der nicht-trivialen Verklebung von g _UV =1 auf einer Überlappung und g _UV =-1 auf der zweiten Überlappung erhält man das nicht-triviale Bündel E , der Möbiusstreifen. Dies kann als "Verdrehen" eines der lokalen Diagramme visualisiert werden.

Gegeben sei ein Vektorbündel E → X vom Rang k und ein Paar Umgebungen U und V, über die das Bündel trivialisiert über

{\begin{ausgerichtet}\varphi_{U}\colon U\times\mathbf{R}^{k}&\mathrel {\xrightarrow {\cong}} \pi^{-1}(U) ,\\\varphi_{V}\colon V\times \mathbf{R}^{k}&\mathrel {\xrightarrow {\cong}} \pi^{-1}(V)\end{ausgerichtet}}

die zusammengesetzte Funktion

\varphi_{U}^{-1}\circ\varphi_{V}\colon (U\cap V)\times \mathbf{R}^{k}\to (U\cap V)\ mal \mathbf{R}^{k}

ist an der Überlappung gut definiert und erfüllt

\varphi_{U}^{-1}\circ \varphi_{V}(x,v)=\left(x,g_{UV}(x)v\right)

für eine GL( k )-wertige Funktion

g_{UV}\colon U\cap V\to \operatorname {GL} (k).

Diese werden die Übergangsfunktionen (oder die Koordinatentransformationen ) des Vektorbündels genannt.

Die Menge der Übergangsfunktionen bildet einen ech-Kocyclus in dem Sinne, dass

g_{UU}(x)=I,\quad g_{UV}(x)g_{VW}(x)g_{WU}(x)=I

für alle U , V , W, über die das Bündel befriedigend trivialisiert . Somit werden die Daten ( E , X , $π$ , R ^k ) definiert ein Faserbündel ; die Zusatzdaten des g _UV spezifizieren eine GL( k )-Strukturgruppe, bei der die Wirkung auf die Faser die Standardwirkung von GL( k ) ist. $U\cap V\cap W\neq \emptyset$

Umgekehrt kann ein Faserbündel gegeben ( E , X , $π$ , R ^k ) mit einer GL ( k ) cocycle in üblichen Weise auf der Faser wirkenden R ^k , wird ein Vektorbündel verbunden. Dies ist ein Beispiel des Faserbündelkonstruktionssatzes für Vektorbündel und kann als alternative Definition eines Vektorbündels genommen werden.

Unterpakete

Ein Linien-Unterbündel eines trivialen Vektorbündels vom Rang 2 über einer eindimensionalen Mannigfaltigkeit .

L

E

M

Eine einfache Methode zum Konstruieren von Vektorbündeln besteht darin, Unterbündel anderer Vektorbündel zu nehmen. Bei einem Vektorbündel über einen topologischen Raum, ein Teilbündel ist einfach ein Unterraum , für die die Einschränkung der zu gibt auch die Struktur eines Vektorbündels. In diesem Fall ist die Faser ein Vektorunterraum für jede . $\pi :E\to X$ $F\subset E$ $\left.\pi \right|_{F}$ $\pi$ $F$ $\left.\pi \right|_{F}:F\to X$ $F_{x}\subset E_{x}$ $x\in X$

Ein Teilbündel eines trivialen Bündels muss nicht trivial sein, und tatsächlich kann jedes reelle Vektorbündel als Teilbündel eines trivialen Bündels von hinreichend hohem Rang angesehen werden. Beispielsweise kann das Möbius-Band , ein nicht-triviales Linienbündel über dem Kreis, als Unterbündel des trivialen Rang-2-Bündels über dem Kreis betrachtet werden.

Vektorbündelmorphismen

Ein Morphismus vom Vektorbündel $π$ ₁ : E ₁ → X ₁ zum Vektorbündel $π$ ₂ : E ₂ → X ₂ ist gegeben durch ein Paar stetiger Abbildungen f : E ₁ → E ₂ und g : X ₁ → X ₂ wie das

g ∘

π

₁ =

π

₂ ∘ f

für jedes x in X ₁ ist die durch f induzierte Abbildung

π

₁⁻¹ ({ x }) →

π

₂⁻¹ ({ g ( x )}) eine lineare Abbildung zwischen Vektorräumen.

Man beachte, dass g durch f bestimmt ist (weil $π$ ₁ surjektiv ist) und f dann g überdeckt .

Die Klasse aller Vektorbündel bildet zusammen mit Bündelmorphismen eine Kategorie . Beschränkt man sich auf Vektorbündel, deren Räume Mannigfaltigkeiten sind (und die Bündelprojektionen sind glatte Abbildungen) und glatte Bündelmorphismen, erhalten wir die Kategorie der glatten Vektorbündel. Vektorbündelmorphismen sind ein Spezialfall des Begriffs einer Bündelabbildung zwischen Faserbündeln und werden oft auch (Vektor-)Bündelhomomorphismen genannt .

Ein Bündel Homomorphismus von E ₁ bis E ₂ mit einer umgekehrten , das auch ein Bündel Homomorphismus ist (von E ₂ bis E ₁ ) ist ein sogenannter (Vektor) Bündel Isomorphismus und dann E ₁ und E ₂ sind die zu isomorphen Vektorbündel. Ein Isomorphismus eines (Rang k ) Vektorbündels E über X mit dem trivialen Bündel (Rang k über X ) heißt Trivialisierung von E , und E heißt dann trivial (oder trivialisierbar ). Die Definition eines Vektorbündels zeigt, dass jedes Vektorbündel lokal trivial ist .

Wir können auch die Kategorie aller Vektorbündel über einem festen Basisraum X betrachten . Als Morphismen in dieser Kategorie nehmen wir jene Morphismen von Vektorbündeln, deren Abbildung auf dem Basisraum die Identitätsabbildung auf X ist . Das heißt, Bündelmorphismen, für die das folgende Diagramm kommutiert :

(Beachten Sie, dass diese Kategorie nicht abelsch ist ; der Kern eines Morphismus von Vektorbündeln ist im Allgemeinen kein Vektorbündel auf natürliche Weise.)

Ein Vektorbündelmorphismus zwischen Vektorbündeln $π$ ₁ : E ₁ → X ₁ und $π$ ₂ : E ₂ → X _2, die eine Abbildung g von X ₁ bis X ₂ abdecken, kann auch als Vektorbündelmorphismus über X ₁ von E ₁ bis aufgefasst werden das Pullback-Bündel g * E ₂ .

Profile und örtlich freie Rollen

Ein Vektorbündel über einer Basis mit Schnitt .

E

M

s

Die Karte , die jedem Punkt auf einer Fläche eine Normale zuordnet, kann man sich als Schnitt vorstellen. Die Fläche ist der Raum X , und an jedem Punkt x befindet sich ein Vektor im Vektorraum, der bei x angehängt ist .

Gegeben ein Vektorbündel $π$ : E → X und eine offene Teilmenge U von X können wir Abschnitte von $π$ auf U betrachten , dh stetige Funktionen s : U → E wobei das zusammengesetzte $π$ ∘ s so ist, dass ( $π$ ∘ s )( u ) = u für alle u in U . Im Wesentlichen weist ein Abschnitt jedem Punkt von U einen Vektor aus dem angeschlossenen Vektorraum kontinuierlich zu. Als Beispiel sind Abschnitte des Tangentialbündels einer Differentialmannigfaltigkeit nichts anderes als Vektorfelder auf dieser Mannigfaltigkeit.

Lassen F ( U ) die Menge aller Abschnitte auf U . F ( U ) enthält immer mindestens ein Element, nämlich den Nullabschnitt : die Funktion s , die jedes Element x von U auf das Nullelement des Vektorraums $π$ ⁻¹ ({ x }) abbildet . Mit der punktweisen Addition und skalaren Multiplikation von Abschnitten wird F ( U ) selbst ein reeller Vektorraum. Die Sammlung dieser Vektorräume ist ein Bündel von Vektorräumen auf X .

Wenn s ein Element von F ( U ) ist und α: U → R eine stetige Abbildung ist, dann ist α s (punktweise Skalarmultiplikation) in F ( U ). Wir sehen, dass F ( U ) ein Modul über dem Ring stetiger reellwertiger Funktionen auf U ist . Wenn außerdem O _X die Strukturgarbe stetiger reellwertiger Funktionen auf X bezeichnet , dann wird F zu einer Garbe von O _X -Modulen.

Nicht jede Garbe von O _X -Modulen entsteht auf diese Weise aus einem Vektorbündel, sondern nur die lokal freien . (Der Grund: lokal suchen wir nach Abschnitten einer Projektion U × R ^k → U ; das sind genau die stetigen Funktionen U → R ^k , und eine solche Funktion ist ein k- Tupel von stetigen Funktionen U → R .)

Mehr noch: die Kategorie des Echtvektorbündels auf X ist äquivalent zu der Kategorie der lokal frei und endlich erzeugten Scheiben von O _X -Module.

Wir können uns also die Kategorie der reellen Vektorbündel auf X so vorstellen , dass sie innerhalb der Kategorie der Garben von O _X- Modulen sitzen ; diese letztere Kategorie ist abelsch, also können wir hier Kernel und Cokernel von Morphismen von Vektorbündeln berechnen.

Ein Vektorbündel vom Rang n ist genau dann trivial, wenn es n linear unabhängige globale Abschnitte hat.

Operationen an Vektorbündeln

Die meisten Operationen auf Vektorräumen können auf Vektorbündel erweitert werden, indem die Vektorraumoperation faserweise ausgeführt wird .

Ist beispielsweise E ein Vektorbündel über X , dann gibt es ein Bündel E* über X , das sogenannte Dualbündel , dessen Faser bei x ∈ X der duale Vektorraum ( E _x )* ist. Formal kann E* als Menge von Paaren ( x , φ) definiert werden, wobei x ∈ X und φ ∈ ( E _x )*. Das duale Bündel ist lokal trivial, weil der duale Raum der Inversen einer lokalen Trivialisierung von E eine lokale Trivialisierung von E* ist : Der entscheidende Punkt hier ist, dass die Operation des dualen Vektorraums funktoriell ist .

Es gibt viele funktionale Operationen, die an Paaren von Vektorräumen (über dem gleichen Körper) ausgeführt werden können, und diese erstrecken sich direkt auf Paare von Vektorbündeln E , F auf X (über dem gegebenen Körper). Es folgen einige Beispiele.

Die Whitney Summe (benannt nach Hassler Whitney ) oder direkte Summe Bündel von E und F ist ein Vektorbündel E ⊕ F über X , deren Faser über x ist die direkte Summe E _x ⊕ F _x der Vektorräume E _x und F _x .
Das Tensorproduktbündel E ⊗ F wird in ähnlicher Weise unter Verwendung des faserweisen Tensorprodukts von Vektorräumen definiert.
Das Hom-Bündel Hom( E , F ) ist ein Vektorbündel, dessen Faser bei x der Raum der linearen Abbildungen von E _x nach F _{x ist} (was oft als Hom( E _x , F _x ) oder L ( E _x , F _x )). Das Hom-Bündel ist so genannt (und nützlich), weil es eine Bijektion zwischen Vektorbündel-Homomorphismen von E nach F über X und Abschnitten von Hom( E , F ) über X gibt .
Aufbauend auf dem vorherigen Beispiel kann man mit einem gegebenen Abschnitt s eines Endomorphismusbündels Hom( E , E ) und einer Funktion f : X → R ein Eigenbündel konstruieren, indem man die Faser über einem Punkt x ∈ X als f ( x )- Eigenraum der linearen Abbildung s ( x ): E _x → E _x . Obwohl diese Konstruktion natürlich ist, wird das resultierende Objekt ohne Sorgfalt keine lokalen Trivialisierungen aufweisen. Betrachten wir den Fall, dass s der Nullabschnitt ist und f isolierte Nullen hat. Die Faser über diesen Nullstellen im resultierenden "Eigenbündel" wird isomorph zu der Faser darüber in E sein , während die Faser überall sonst der triviale 0-dimensionale Vektorraum ist.
Das duale Vektorbündel E* ist das Hom-Bündel Hom( E , R × X ) der Bündelhomomorphismen von E und das triviale Bündel R × X . Es gibt einen kanonischen Vektorbündelisomorphismus Hom( E , F ) = E* ⊗ F .

Jede dieser Operationen ist ein besonderes Beispiel für ein allgemeines Merkmal von Bündeln: dass viele Operationen, die an der Kategorie der Vektorräume durchgeführt werden können, auch an der Kategorie der Vektorbündel auf funktionale Weise ausgeführt werden können. Dies wird in der Sprache glatter Funktoren präzisiert . Eine Operation anderer Art ist die Pullback-Bundle- Konstruktion. Gegeben ein Vektorbündel E → Y und eine stetige Abbildung f : X → Y kann man E auf ein Vektorbündel f*E über X "zurückziehen" . Die Faser über einen Punkt x ∈ X ist im Wesentlichen nur die Faser über f ( x ) ∈ Y . Daher Whitney Summiereinrichtung E ⊕ F kann als Rücksetzer Bündel der diagonalen Karte definiert werden , von X zu X × X , wo das Bündel über X × X ist E × F .

Bemerkung : Sei X ein kompakter Raum. Jedes Vektorbündel E über X ist ein direkter Summand eines trivialen Bündels; dh es existiert ein Bündel E ‚ so dass E ⊕ E ‘ trivial. Dies schlägt fehl, wenn X nicht kompakt ist: zum Beispiel hat das tautologische Linienbündel über dem unendlichen reellen projektiven Raum diese Eigenschaft nicht.

Zusätzliche Strukturen und Verallgemeinerungen

Vektorbündeln wird oft mehr Struktur gegeben. Zum Beispiel können Vektorbündel mit einer Vektorbündelmetrik ausgestattet sein . Normalerweise muss diese Metrik positiv definit sein , in diesem Fall wird jede Faser von E ein euklidischer Raum. Ein Vektorbündel mit komplexer Struktur entspricht einem komplexen Vektorbündel , das auch dadurch erhalten werden kann, dass reelle Vektorräume in der Definition durch komplexe ersetzt werden und alle Abbildungen in den Fasern komplex-linear sein müssen. Allgemeiner kann man die einem Vektorbündel auferlegte zusätzliche Struktur typischerweise im Hinblick auf die resultierende Reduzierung der Strukturgruppe eines Bündels verstehen . Vektorbündel über allgemeinere topologische Felder können ebenfalls verwendet werden.

Nimmt man statt eines endlichdimensionalen Vektorraums die Faser F als Banach-Raum, so erhält man ein Banach-Bündel . Konkret muss man fordern, dass die lokalen Trivialisierungen Banachraum-Isomorphismen (und nicht nur lineare Isomorphismen) auf jeder der Fasern sind und dass außerdem die Übergänge

g_{UV}\colon U\cap V\to \operatorname {GL} (F)

sind stetige Abbildungen von Banachmannigfaltigkeiten . In der entsprechenden Theorie für C ^p -Bündel müssen alle Abbildungen C ^{p sein} .

Vektorbündel sind spezielle Faserbündel , deren Fasern Vektorräume sind und deren Kozykel die Vektorraumstruktur respektiert. Es können allgemeinere Faserbündel konstruiert werden, bei denen die Faser andere Strukturen aufweisen kann; beispielsweise Kugelbündel werden durch Kugeln fibered.

Glatte Vektorbündel

Die Regelmäßigkeit von Übergangsfunktionen, die ein Vektorbündel beschreiben, bestimmt die Art des Vektorbündels. Bei Verwendung der stetigen Übergangsfunktionen g _UV ist das resultierende Vektorbündel E nur stetig, aber nicht glatt. Werden die glatten Übergangsfunktionen h _UV verwendet, so ist das resultierende Vektorbündel F ein glattes Vektorbündel.

Ein Vektor Bündel ( E , P , M ) ist glatt , wenn E und M sind glatte Verteilern , p: E → M eine glatte Karte ist, und die lokalen Trivialisierungen sind Diffeomorphismen . Je nach dem erforderlichen Grad an Glätte, gibt es verschiedene entsprechende Vorstellungen von C ^p Bündeln, unendlich differenzierbare C ^∞ -bundles und reale analytische C ^ω -bundles. In diesem Abschnitt konzentrieren wir uns auf C ^∞ -Bündel. Das wichtigste Beispiel für ein C ^∞ -vector Bündel ist die Tangentialbündel ( TM , $π$ _TM , M ) ein C ^∞ Mannigfaltigkeit M .

Ein glattes Vektorbündel kann dadurch charakterisiert werden, dass es Übergangsfunktionen wie oben beschrieben zulässt, die glatte Funktionen auf Überlappungen von trivialisierenden Diagrammen U und V sind . Das heißt, ein Vektorbündel E ist glatt, wenn es eine Überdeckung durch Trivialisierung offener Mengen zulässt, so dass für zwei beliebige solcher Mengen U und V die Übergangsfunktion

g_{UV}:U\cap V\to \operatorname {GL} (k,\mathbb{R} )

ist eine glatte Funktion in die Matrixgruppe GL(k, R ), die eine Lie-Gruppe ist .

Ähnlich sind die Übergangsfunktionen:

C ^r dann ist das Vektorbündel ein C ^r -Vektorbündel ,
reell analytisch, dann ist das Vektorbündel ein reelles analytisches Vektorbündel (dafür muss die Matrixgruppe eine reelle analytische Struktur haben),
holomorph, dann ist das Vektorbündel ein holomorphes Vektorbündel (dafür muss die Matrixgruppe eine komplexe Lie-Gruppe sein ),
algebraische Funktionen dann ist das Vektorbündel ein algebraisches Vektorbündel (dafür muss die Matrixgruppe eine algebraische Gruppe sein ).

Die C ^∞ -vector Bündel ( E , p , M ) hat eine sehr wichtige Eigenschaft nicht durch allgemeinere geteilt C ^∞ -fibre Bundles. Nämlich der Tangentenraum T _v ( E _x ) zu jedem v ∈ E _x kann natürlich mit der Faser identifiziert werden E _x selbst. Diese Identifikation erhält man durch den vertikalen Auftrieb vl _v : E _x → T _v ( E _x ), definiert als

\operatorname {vl} _{v}w[f]:=\left.{\frac {d}{dt}}\right|_{t=0}f(v+tw),\quad f \in C^{\infty}(E_{x}).

Der vertikale Auftrieb kann auch als natürlicher C ^∞ -Vektorbündelisomorphismus p*E → VE angesehen werden , wobei ( p*E , p*p , E ) das Rückzugsbündel von ( E , p , M ) über E . ist durch p : E → M , und VE := Ker( p _* ) TE ist das vertikale Tangentialbündel , ein natürliches Vektorunterbündel des Tangentialbündels ( TE , $π$ _TE , E ) des Gesamtraums E .

Der Gesamtraum E eines glatten Vektorbündels trägt ein natürliches Vektorfeld V _v := vl _v v , das sogenannte kanonische Vektorfeld . Formaler ist V ein glatter Abschnitt von ( TE , $π$ _TE , E ) und kann auch als infinitesimaler Generator der Lie-Gruppenwirkung ( t , v ) ↦ e ^t v durch die faserweise Skalarmultiplikation definiert werden. Das kanonische Vektorfeld V charakterisiert vollständig die glatte Vektorbündelstruktur auf folgende Weise. Als Vorbereitung zu beachten , dass , wenn X ein glattes Vektorfeld auf einem glatten Mannigfaltigkeit M und x ∈ M , so daß X _x = 0 ist , die linearen Abbildungs

C_{x}(X):T_{x}M\to T_{x}M;\quad C_{x}(X)Y=(\nabla_{Y}X)_{x}

hängt nicht von der Wahl der linearen kovarianten Ableitung ∇ auf M ab . Das kanonische Vektorfeld V auf E erfüllt die Axiome

Der Fluss ( t , v ) → ^t_V ( v ) von V ist global definiert.
Für jedes v ∈ V gibt es einen eindeutigen lim _t→∞ Φ ^t_V ( v ) ∈ V .
C _v ( V )∘ C _v ( V ) = C _v ( V ), wenn V _v = 0.
Die Nullmenge von V ist eine glatte Untermannigfaltigkeit von E, deren Kodimension gleich dem Rang von C _v ( V ) ist.

Umgekehrt, wenn E eine beliebige glatte Mannigfaltigkeit und V ein glattes Vektorfeld auf E ist , das 1–4 erfüllt, dann gibt es eine eindeutige Vektorbündelstruktur auf E, deren kanonisches Vektorfeld V ist .

Für jedes glatte Vektorbündel ( E , p , M ) hat der Gesamtraum TE seines Tangentenbündels ( TE , $π$ _TE , E ) eine natürliche sekundäre Vektorbündelstruktur ( TE , p _* , TM ), wobei p _* der Schub -Vorwärts der kanonischen Projektion p : E → M . Die Vektorbündeloperationen in dieser sekundären Vektorbündelstruktur sind die Push-Forwards + _* : T ( E × E ) → TE und λ _* : TE → TE der ursprünglichen Addition +: E × E → E und Skalarmultiplikation λ: E → E .

K-Theorie

Die K-Theorie - Gruppe, $K (X)$ , von einem kompakten Hausdorff topologischen Raum wird als die abelschen Gruppe , die durch Isomorphieklassen erzeugt definiert $[E]$ des komplexen Vektorbündels modulo die Beziehung , daß , wenn wir haben eine genaue Abfolge

0\nach A\nach B\nach C\nach 0

dann

[B]=[A]+[C]

in der topologischen K-Theorie . Die KO-Theorie ist eine Version dieser Konstruktion, die reelle Vektorbündel betrachtet. K-Theorie mit kompakten Trägern kann ebenso definiert werden wie höhere K-Theorie-Gruppen.

Der berühmte Periodizitätssatz von Raoul Bott behauptet, dass die K-Theorie jedes Raumes $X$ isomorph zu der des $S 2 X ist$ , der doppelten Aufhängung von $X$ .

In der algebraischen Geometrie betrachtet man die K-Theorie-Gruppen bestehend aus kohärenten Garben auf einem Schema $X$ sowie die K-Theorie-Gruppen von Vektorbündeln auf dem Schema mit obiger Äquivalenzrelation. Die beiden Konstrukte sind gleich, vorausgesetzt, das zugrunde liegende Schema ist glatt .

Siehe auch

Allgemeine Begriffe

Grassmannian : Klassifikationsräume für Vektorbündel, darunter projektive Räume für Linienbündel
Merkmalsklasse
Spaltprinzip
Stabiles Bündel

Topologie und Differentialgeometrie

Eichtheorie : das allgemeine Studium der Zusammenhänge von Vektorbündeln und Hauptbündeln und ihre Beziehungen zur Physik.
Verbindung : Der Begriff, der benötigt wird, um Abschnitte von Vektorbündeln zu unterscheiden.

Algebraische und analytische Geometrie

Anmerkungen

Quellen

Abraham, Ralph H .; Marsden, Jerrold E. (1978), Grundlagen der Mechanik , London: Benjamin-Cummings, siehe Abschnitt 1.5, ISBN 978-0-8053-0102-1.
Hatcher, Allen (2003), Vektorbündel & K-Theorie (2.0 Aufl.).
Jost, Jürgen (2002), Riemannian Geometry and Geometric Analysis (3. Aufl.), Berlin, New York: Springer-Verlag , ISBN 978-3-540-42627-1, siehe Abschnitt 1.5.
Lang, Serge (1995), Differentielle und Riemannsche Mannigfaltigkeiten , Berlin, New York: Springer-Verlag , ISBN 978-0-387-94338-1.
Lee, Jeffrey M. (2009), Mannigfaltigkeiten und Differentialgeometrie , Graduate Studies in Mathematics , Vol. 2, No. 107, Providence: American Mathematical Society, ISBN 978-0-8218-4815-9 |volume=hat zusätzlichen Text ( Hilfe ).
Lee, John M. (2003), Einführung in glatte Verteiler , New York: Springer, ISBN 0-387-95448-1 siehe Kap.5
Rubei, Elena (2014), Algebraische Geometrie, ein kurzes Wörterbuch , Berlin/Boston: Walter De Gruyter, ISBN 978-3-11-031622-3.

Languages

In other projects