Modulraum - Moduli space

In der Mathematik , insbesondere der algebraischen Geometrie , ist ein Modulraum ein geometrischer Raum (normalerweise ein Schema oder ein algebraischer Stapel ), dessen Punkte algebro-geometrische Objekte einer festen Art oder Isomorphismusklassen solcher Objekte darstellen. Solche Räume treten häufig als Lösung von Klassifikationsproblemen auf: Kann man zeigen, dass eine Sammlung interessanter Objekte (z. B. die glatten algebraischen Kurven einer festen Gattung) die Struktur eines geometrischen Raums erhalten, dann kann man solche Objekte parametrisieren, indem man Koordinaten auf dem resultierenden Raum einführt. Der Begriff "Modul" wird in diesem Zusammenhang synonym mit "Parameter" verwendet; Modulräume wurden zunächst eher als Räume von Parametern denn als Räume von Objekten verstanden. Eine Variante von Modulräumen sind formale Moduli .

Motivation

Modulräume sind Lösungsräume geometrischer Klassifikationsprobleme. Das heißt, die Punkte eines Modulraums entsprechen Lösungen geometrischer Probleme. Hier werden verschiedene Lösungen identifiziert, wenn sie isomorph (dh geometrisch gleich) sind. Modulräume kann man sich als einen universellen Parameterraum für das Problem vorstellen. Betrachten Sie zum Beispiel das Problem, alle Kreise in der euklidischen Ebene bis zur Kongruenz zu finden. Jeder Kreis kann eindeutig beschrieben werden, indem drei Punkte angegeben werden, aber viele verschiedene Mengen von drei Punkten ergeben den gleichen Kreis: die Entsprechung ist n:1. Kreise werden jedoch eindeutig parametrisiert, indem ihr Mittelpunkt und ihr Radius angegeben werden: Dies sind zwei reelle Parameter und ein positiver reeller Parameter. Da uns nur Kreise "bis zur Kongruenz" interessieren, identifizieren wir Kreise mit unterschiedlichen Mittelpunkten, aber gleichem Radius, so dass der Radius allein ausreicht, um die interessierende Menge zu parametrisieren. Der Modulraum sind also die positiven reellen Zahlen .

Modulräume tragen oft auch natürliche geometrische und topologische Strukturen. Im Beispiel von Kreisen beispielsweise ist der Modulraum nicht nur eine abstrakte Menge, sondern der Absolutwert der Differenz der Radien definiert eine Metrik zur Bestimmung, wann zwei Kreise "nahe" sind. Die geometrische Struktur von Modulräumen sagt uns lokal, wann zwei Lösungen eines geometrischen Klassifikationsproblems "nahe" sind, aber im Allgemeinen haben Modulräume auch eine komplizierte globale Struktur.

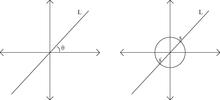
Überlegen Sie beispielsweise, wie Sie die Sammlung von Linien in R ^{2 beschreiben,} die den Ursprung schneiden. Wir wollen jeder Linie L dieser Familie eine Größe zuordnen , die sie eindeutig identifizieren kann – einen Modul. Ein Beispiel für eine solche Größe ist der positive Winkel θ( L ) mit 0 ≤ θ < π Radiant. Die so parametrisierte Menge der Linien L ist als P ¹ ( R ) bekannt und wird als die reelle projektive Linie bezeichnet .

Wir können die Ansammlung von Linien in R ² , die den Ursprung schneiden, auch durch eine topologische Konstruktion beschreiben. Nämlich: betrachten S ¹ ⊂ R ² und bemerke , dass jeder Punkt s ∈ S ¹ eine Linie ergibt L ( s ) in der Sammlung (die den Ursprung tritt und s ). Diese Abbildung ist jedoch zwei zu eins, also wollen wir s ~ − s identifizieren , um P ¹ ( R ) ≅ S ¹ /~ zu erhalten, wobei die Topologie auf diesem Raum die Quotiententopologie ist, die durch die Quotientenabbildung S ¹ → P ¹ ( R ).

Wenn wir also P ¹ ( R ) als einen Modulraum von Geraden betrachten, die den Ursprung in R ² schneiden , erfassen wir die Möglichkeiten, wie die Mitglieder (in diesem Fall die Geraden) der Familie modulieren können, indem wir 0 ≤ θ < . kontinuierlich variieren .

Grundlegende Beispiele

Projektiver Raum und Grassmannianer

Der reelle projektive Raum P ⁿ ist ein Modulraum, der den Raum der Linien in R ^{n +1} parametrisiert, die durch den Ursprung gehen. In ähnlicher Weise ist der komplexe projektive Raum der Raum aller komplexen Linien in C ^{n +1,} die durch den Ursprung gehen.

Allgemeiner gesagt , die Grassmannsche G ( K , V ) ein Vektorraum V über ein Feld F ist der Modulraum aller k -dimensionalen linearen Unterräume von V .

Projektiver Raum als Modul sehr großer Linienbündel mit global erzeugten Schnitten

Immer wenn ein Schema in den universellen projektiven Raum eingebettet wird, ist die Einbettung durch ein Linienbündel und Abschnitte gegeben, die nicht alle gleichzeitig verschwinden. Dies bedeutet, dass ein Punkt gegeben ist${\displaystyle X}$${\displaystyle \mathbf{P}_{\mathbb{Z}}^{n}}$${\displaystyle {\mathcal {L}}\to X}$${\displaystyle n+1}$${\displaystyle s_{0},\ldots,s_{n}\in\Gamma(X,{\mathcal{L}})}$

${\displaystyle x:{\text{Spec}}(R)\to X}$

es gibt einen zugehörigen Punkt

${\displaystyle {\hat{x}}:{\text{Spec}}(R)\to \mathbf{P} _{\mathbb{Z}}^{n}}$

gegeben durch die Kompositionen

${\displaystyle [s_{0}:\cdots :s_{n}]\circ x=[s_{0}(x):\cdots :s_{n}(x)]\in \mathbf {P} _{ \mathbb{Z}}^{n}(R)}$

Dann sind zwei Linienbündel mit Abschnitten äquivalent

${\displaystyle ({\mathcal{L}},(s_{0},\ldots,s_{n}))\sim ({\mathcal{L}}',(s_{0}',\ldots,s_ {n}'))}$

wenn es einen Isomorphismus gibt, so dass . Dies bedeutet, dass der zugehörige Moduli-Funktor${\displaystyle \phi:{\mathcal{L}}\to {\mathcal{L}}'}$${\displaystyle \phi(s_{i})=s_{i}'}$

${\displaystyle \mathbf {P} _{\mathbb {Z} }^{n}:{\text{Sch}}\to {\text{Mengen}}}$

sendet ein Schema an das Set${\displaystyle X}$

${\displaystyle\mathbf{P}_{\mathbb{Z}}^{n}(X)=\left\{({\mathcal{L}},s_{0},\ldots,s_{n}) :{\begin{matrix}{\mathcal{L}}\to X{\text{ ist ein Linienbündel}}\\s_{0},\ldots ,s_{n}\in \Gamma (X,{\ mathcal {L}})\\{\text{ bilden eine Basis von globalen Abschnitten}}\end{matrix}}\right\}/\sim }$

Um zu zeigen, dass dies wahr ist, können Sie eine Reihe von Tautologien durchlaufen: Jede projektive Einbettung ergibt die global generierte Garbe mit Abschnitten . Umgekehrt ergibt ein von Abschnitten global erzeugtes umfangreiches Linienbündel eine Einbettung wie oben. ${\displaystyle i:X\to\mathbb{P}_{\mathbb{Z}}^{n}}$${\displaystyle i^{*}{\mathcal{O}}_{\mathbf{P} _{\mathbb{Z}}^{n}}(1)}$${\displaystyle i^{*}x_{0},\ldots ,i^{*}x_{n}}$${\displaystyle {\mathcal {L}}\to X}$${\displaystyle n+1}$

Chow-Vielfalt

Die Chow-Varietät Chow (d, P ³ ) ist eine projektive algebraische Varietät, die Kurven des Grades d in P ³ parametrisiert . Es ist wie folgt aufgebaut. Sei C eine Kurve vom Grad d in P ³ , dann betrachte alle Geraden in P ³ , die die Kurve C schneiden . Dies ist ein Divisor Grad d D _C in G (2, 4), die Grassmannsche Linien in P ³ . Wenn C variiert, erhalten wir durch Assoziieren von C mit D _C einen Parameterraum von Kurven vom Grad d als Teilmenge des Raums von Teilern vom Grad d des Grassmann-Operators: Chow (d, P ³ ).

Hilbert-Schema

Das Hilbert-Schema Hilb ( X ) ist ein Moduli-Schema. Jeder abgeschlossene Punkt von Hilb ( X ) entspricht einem abgeschlossenen Unterschema eines festen Schemas X , und jedes abgeschlossene Unterschema wird durch einen solchen Punkt repräsentiert. Ein einfaches Beispiel für ein Hilbert-Schema ist das Hilbert-Schema, das Gradhyperflächen des projektiven Raums parametrisiert . Dies ist gegeben durch das projektive Bündel${\displaystyle d}$${\displaystyle \mathbb{P}^{n}}$

${\displaystyle {\mathcal{Hilb}}_{d}(\mathbb{P}^{n})=\mathbb{P} (\Gamma ({\mathcal{O}}(d))}$

mit universeller Familie gegeben von

${\displaystyle {\mathcal{U}}=\{(V(f),f):f\in\Gamma ({\mathcal{O}}(d))\}}$

wobei das zugehörige projektive Schema für das homogene Polynom des Grades ist . ${\displaystyle V(f)}$${\displaystyle d}$${\displaystyle f}$

Definitionen

Es gibt mehrere verwandte Begriffe von Dingen, die wir Modulräume nennen könnten. Jede dieser Definitionen formalisiert eine andere Vorstellung davon, was es für die Punkte des Raums M bedeutet , geometrische Objekte darzustellen.

Feinmodulräume

Dies ist das Standardkonzept. Wenn wir einen Raum M haben, für den jeder Punkt m ∊ M einem algebro-geometrischen Objekt U _{m entspricht} , können wir diese Objekte heuristisch zu einer tautologischen Familie U über M zusammenfassen . (Zum Beispiel trägt der Grassmannsche G ( k , V ) ein Bündel vom Rang k , dessen Faser an jedem Punkt [ L ] ∊ G ( k , V ) einfach der lineare Unterraum L ⊂ V ist .) M heißt Basisraum der Familie U . Wir sagen , dass eine solche Familie ist universell , wenn eine Familie von Algebro-geometrische Objekte T über einen beliebigen Basis Raum B das ist Pullback von U entlang einer einzigartigen Karte B → M . Ein feiner Modulraum ist ein Raum M, der die Basis einer universellen Familie ist.

Nehmen wir genauer an, wir haben einen Funktor F von Schemata zu Mengen, der einem Schema B die Menge aller geeigneten Objektfamilien mit Basis B zuordnet . Ein Raum M ist ein Feinmodulraum für den Funktor F, wenn M für F steht , dh es gibt einen natürlichen Isomorphismus τ : F → Hom (−, M ), wobei Hom (−, M ) der Funktor der Punkte ist. Dies impliziert, dass M eine universelle Familie trägt; diese Familie ist die Familie auf M , die der Identitätskarte 1 _M ∊ Hom ( M , M ) entspricht.

Grobe Modulräume

Feine Modulräume sind wünschenswert, aber sie existieren nicht immer und sind häufig schwer zu konstruieren, daher verwenden Mathematiker manchmal einen schwächeren Begriff, die Idee eines groben Modulraums. Ein Raum M ist ein grober Modulraum für den Funktor F, wenn es eine natürliche Transformation τ : F → Hom (−, M ) gibt und τ unter solchen natürlichen Transformationen universell ist. Genauer gesagt ist M ein grober Modulraum für F, wenn jede Familie T über einer Basis B eine Abbildung φ _T  : B → M ergibt und zwei beliebige Objekte V und W (als Familien über einem Punkt betrachtet) dem gleichen Punkt entsprechen von M genau dann, wenn V und W isomorph sind. Somit ist M ein Raum, der für jedes Objekt, das in einer Familie vorkommen könnte, einen Punkt hat und dessen Geometrie die Art und Weise widerspiegelt, wie Objekte in Familien variieren können. Beachten Sie jedoch, dass ein grober Modulraum nicht unbedingt eine Familie geeigneter Objekte trägt, geschweige denn eine universelle.

Mit anderen Worten umfasst ein feiner Modulraum sowohl einen Basisraum M als auch eine universelle Familie U → M , während ein grober Modulraum nur den Basisraum M hat .

Modulstapel

Es kommt häufig vor, dass interessante geometrische Objekte mit vielen natürlichen Automorphismen ausgestattet sind . Dies macht insbesondere die Existenz eines feinen Modulraums unmöglich (intuitiv ist die Idee, dass, wenn L ein geometrisches Objekt ist, die triviale Familie L × [0,1] in eine verdrehte Familie auf dem Kreis S ^{1 umgewandelt werden kann,} indem man identifiziert L × {0} mit L × {1} über einen nichttrivialen Automorphismus. Wenn nun ein feiner Modulraum X existierte, sollte die Abbildung S ¹ → X nicht konstant sein, sondern müsste durch Trivialität auf jeder echten offenen Menge konstant sein) , kann man manchmal noch einen groben Modulraum erhalten. Dieser Ansatz ist jedoch nicht ideal, da die Existenz solcher Räume nicht garantiert ist, sie häufig singulär sind, wenn sie existieren, und Details über einige nicht-triviale Familien von Objekten, die sie klassifizieren, übersehen.

Ein ausgeklügelterer Ansatz besteht darin, die Klassifikation durch Erinnern an die Isomorphismen anzureichern. Genauer gesagt kann man auf jeder Basis B die Kategorie der Familien auf B betrachten, wobei nur Isomorphismen zwischen Familien als Morphismen angesehen werden. Man betrachtet dann die faserige Kategorie, die jedem Raum B das Gruppoid der Familien über B zuordnet . Die Verwendung dieser in Gruppoiden gefaserten Kategorien zur Beschreibung eines Moduliproblems geht auf Grothendieck (1960/61) zurück. Im Allgemeinen können sie nicht durch Schemata oder gar algebraische Räume dargestellt werden , aber in vielen Fällen haben sie eine natürliche Struktur eines algebraischen Stapels .

Algebraische Stapel und ihre Verwendung zur Analyse von Modulproblemen sind in Deligne-Mumford (1969) als Werkzeug zum Nachweis der Irreduzibilität des (groben) Modulraums von Kurven einer bestimmten Gattung erschienen. Die Sprache der algebraischen Stapel bietet im Wesentlichen eine systematische Möglichkeit, die faserige Kategorie, die das Modulproblem darstellt, als "Raum" zu betrachten, und der Modulstapel vieler Modulprobleme verhält sich besser (wie glatt) als der entsprechende grobe Modulraum.

Weitere Beispiele

Kurvenmodul

Der Modulstack klassifiziert Familien glatter projektiver Kurven der Gattung g zusammen mit ihren Isomorphismen. Wenn g > 1 ist, kann dieser Stapel verdichtet werden, indem neue "Rand"-Punkte hinzugefügt werden, die stabilen Knotenkurven (zusammen mit ihren Isomorphismen) entsprechen. Eine Kurve ist stabil, wenn sie nur eine endliche Gruppe von Automorphismen hat. Der resultierende Stapel wird mit bezeichnet . Beide Modulstapel tragen universelle Kurvenscharen. Man kann auch grobe Modulräume definieren, die Isomorphismusklassen von glatten oder stabilen Kurven darstellen. Diese groben Modulräume wurden tatsächlich untersucht, bevor der Begriff des Modulstapels erfunden wurde. Tatsächlich wurde die Idee eines Modulstapels von Deligne und Mumford erfunden, um die Projektivität der groben Modulräume zu beweisen. In den letzten Jahren hat sich gezeigt, dass der Kurvenstapel tatsächlich das grundlegendere Objekt ist. ${\displaystyle {\mathcal{M}}_{g}}$${\displaystyle {\overline {\mathcal {M}}}_{g}}$

Beide Stapel oben haben die Dimension 3 g -3; daher kann eine stabile Knotenkurve vollständig spezifiziert werden, indem die Werte von 3 g −3 Parametern gewählt werden, wenn g > 1. In der unteren Gattung muss man das Vorhandensein glatter Familien von Automorphismen durch Subtrahieren ihrer Anzahl berücksichtigen. Es gibt genau eine komplexe Kurve der Gattung Null, die Riemannsche Kugel, und ihre Isomorphismengruppe ist PGL(2). Daher ist die Dimension von is ${\displaystyle {\mathcal {M}}_{0}}$

dim(Raum der Genus-Null-Kurven) − dim(Gruppe von Automorphismen) = 0 − dim(PGL(2)) = −3.

Ebenso gibt es in der Gattung 1 einen eindimensionalen Kurvenraum, aber jede solche Kurve hat eine eindimensionale Gruppe von Automorphismen. Der Stapel hat also die Dimension 0. Die groben Modulräume haben die Dimension 3 g −3 wie die Stapel für g > 1, weil die Kurven mit der Gattung g > 1 nur eine endliche Gruppe als Automorphismus haben, dh dim(eine Gruppe von Automorphismen) = 0. Schließlich hat der Grobmodulraum in der Gattung null die Dimension null und in der Gattung eins die Dimension eins. ${\displaystyle {\mathcal{M}}_{1}}$

Man kann das Problem auch bereichern, indem man den Modulstapel von Genus- g- Knotenkurven mit n markierten Punkten betrachtet. Solche markierten Kurven werden als stabil bezeichnet, wenn die Untergruppe der Kurvenautomorphismen, die die markierten Punkte fixieren, endlich ist. Die resultierenden Modulstapel von glatten (oder stabilen) Kurven der Gattung g mit n- markierten Punkten werden mit (oder ) bezeichnet und haben die Dimension 3 g  − 3 +  n . ${\displaystyle {\mathcal{M}}_{g,n}}$${\displaystyle {\overline {\mathcal {M}}}_{g,n}}$

Von besonderem Interesse ist der Modulstack von Genus 1-Kurven mit einem markierten Punkt. Dies ist der Stapel elliptischer Kurven und ist die natürliche Heimat der viel untersuchten modularen Formen , die meromorphe Abschnitte von Bündeln auf diesem Stapel sind. ${\displaystyle {\overline {\mathcal {M}}}_{1,1}}$

Moduli der Sorten

In höheren Dimensionen sind Moduli algebraischer Varietäten schwieriger zu konstruieren und zu studieren. Zum Beispiel ist das höherdimensionale Analogon des oben diskutierten Modulraums elliptischer Kurven der Modulraum abelscher Varietäten, wie der Siegel-Modularvarietät . Dies ist das Problem, das der modularen Formtheorie von Siegel zugrunde liegt . Siehe auch Shimura-Sorte .

Moduli von Vektorbündeln

Ein weiteres wichtiges Modulproblem besteht darin, die Geometrie (verschiedener Teilstapel von) des Modulstapels Vect _n ( X ) von Vektorbündeln vom Rang n auf einer festen algebraischen Varietät X zu verstehen . Dieser Stapel wurde am besten untersucht, wenn X eindimensional ist und insbesondere, wenn n gleich eins ist. In diesem Fall ist der grobe Modulraum das Picard-Schema , das wie der Modulraum von Kurven untersucht wurde, bevor Stapel erfunden wurden. Wenn die Bündel den Rang 1 und den Grad Null haben, ist das Studium des groben Modulraums das Studium der Jacobi-Varietät .

Bei Anwendungen in der Physik hat sich die Modulzahl von Vektorbündeln und das eng damit verbundene Problem der Modulzahl von Haupt-G-Bündeln als bedeutsam in der Eichtheorie erwiesen .

Volumen des Modulraums

Einfache Geodäten und Weil-Petersson- Volumen von Modulräumen von umrandeten Riemann-Flächen.

Methoden zur Konstruktion von Modulräumen

Die moderne Formulierung von Moduli-Problemen und die Definition von Moduli-Räumen in Form der Moduli-Funktoren (oder allgemeiner der in Gruppoiden gefaserten Kategorien ) und der sie (fast) repräsentierenden Räume geht auf Grothendieck (1960/61) zurück, in dem er allgemeine Rahmenbedingungen, Ansätze und Hauptprobleme am Beispiel von Teichmüller-Räumen in komplexer analytischer Geometrie. Die Vorträge beschreiben insbesondere die allgemeine Methode zur Konstruktion von Modulräumen, indem zunächst das betrachtete Modulproblem versteift wird .

Genauer gesagt macht es die Existenz nichttrivialer Automorphismen der zu klassifizierenden Objekte unmöglich, einen feinen Modulraum zu haben. Es ist jedoch oft möglich, ein modifiziertes Modulproblem der Klassifizierung der ursprünglichen Objekte zusammen mit zusätzlichen Daten in Betracht zu ziehen, die so gewählt sind, dass die Identität der einzige Automorphismus ist, der auch die zusätzlichen Daten berücksichtigt. Bei geeigneter Wahl der erstarrenden Daten hat das modifizierte Modulproblem einen (feinen) Modulraum T , der oft als Unterschema eines geeigneten Hilbert- oder Quot-Schemas beschrieben wird . Die erstarrenden Daten sind zudem so gewählt, dass sie einem Hauptbündel mit einer algebraischen Strukturgruppe G entsprechen . Somit kann man vom erstarrten Problem zum Original zurückkehren, indem man den Quotienten durch die Wirkung von G bildet , und das Problem der Konstruktion des Modulraums wird zu dem, ein Schema (oder einen allgemeineren Raum) zu finden, das (in einem angemessen starken Sinne) der Quotient T / G von T durch die Wirkung von G . Das letzte Problem lässt im Allgemeinen keine Lösung zu; es wird jedoch von der bahnbrechenden geometrischen Invariantentheorie (GIT) adressiert , die 1965 von David Mumford entwickelt wurde und zeigt, dass der Quotient unter geeigneten Bedingungen tatsächlich existiert.

Um zu sehen, wie dies funktionieren könnte, betrachten wir das Problem der Parametrisierung von glatten Kurven der Gattung g > 2. Eine glatte Kurve zusammen mit einem vollständigen linearen System vom Grad d > 2 g ist äquivalent zu einem abgeschlossenen eindimensionalen Unterschema des projektiven Raums P ^{d −g} . Folglich kann der Modulraum glatter Kurven und linearer Systeme (die bestimmten Kriterien genügen) in das Hilbert-Schema eines ausreichend hochdimensionalen projektiven Raums eingebettet werden. Dieser Locus H im Hilbert-Schema hat eine Wirkung von PGL( n ), die die Elemente des linearen Systems mischt; folglich ergibt sich der Modulraum glatter Kurven als Quotient von H durch die projektive allgemeine lineare Gruppe.

Ein anderer allgemeiner Ansatz ist vor allem mit Michael Artin verbunden . Hier geht es darum, von einem zu klassifizierenden Objekt auszugehen und seine Deformationstheorie zu studieren . Das bedeutet, zunächst infinitesimale Deformationen zu konstruieren und dann auf Prorepräsentabilitätssätze zurückzugreifen , um diese über eine formale Basis zu einem Objekt zusammenzusetzen . Als nächstes liefert ein Appell an den formalen Existenzsatz von Grothendieck ein Objekt der gewünschten Art über einer Basis, die ein vollständiger lokaler Ring ist. Dieses Objekt kann über das Näherungstheorem von Artin durch ein über einem endlich erzeugten Ring definiertes Objekt approximiert werden . Das Spektrum dieses letztgenannten Rings kann dann als eine Art Koordinatendiagramm auf dem gewünschten Modulraum angesehen werden. Indem wir genügend dieser Diagramme zusammenkleben, können wir den Raum abdecken, aber die Karte von unserer Vereinigung der Spektren zum Modulraum wird im Allgemeinen viele zu eins sein. Wir definieren daher eine Äquivalenzrelation auf ersterem; im Wesentlichen sind zwei Punkte äquivalent, wenn die Objekte über jedem isomorph sind. Dies ergibt ein Schema und eine Äquivalenzrelation, die ausreichen, um einen algebraischen Raum (eigentlich einen algebraischen Stapel, wenn wir vorsichtig sind) zu definieren, wenn nicht immer ein Schema.

In Physik

Der Begriff Modulraum wird manchmal in der Physik verwendet, um sich speziell auf den Modulraum von Vakuum-Erwartungswerten einer Menge von Skalarfeldern oder auf den Modulraum möglicher String-Hintergründe zu beziehen .

Modulräume treten auch in der Physik in der topologischen Feldtheorie auf , wo man Feynman-Pfadintegrale verwenden kann , um die Schnittzahlen verschiedener algebraischer Modulräume zu berechnen .

Siehe auch

Bauwerkzeuge

• Hilbert-Schema
• Quotierungsschema
• Verformungstheorie
• GIT-Quotient
• Artin-Kriterium , allgemeines Kriterium zur Konstruktion von Modulräumen als algebraische Stapel aus Modulfunktoren

Modulräume

• Modul algebraischer Kurven
• Modulstapel elliptischer Kurven
• Modulare Kurve
• Picard-Funktor
• Moduli halbstabiler Seilscheiben auf einer Kurve
• Kontsevich-Modulraum
• Moduli von halbstabilen Seilscheiben

Verweise

Anmerkungen

• Modultheorie

Forschungsartikel

Grundlagenpapiere

• Grothendieck, Alexander (1960–1961). "Techniques de construction en géométrie analytique. I. Beschreibung axiomatique de l'espace de Teichmüller et de ses variables" (PDF) . Séminaire Henri Cartan 13 Nr. 1, Exposés Nr. 7 und 8 . Paris.

• Mumford, David , Geometrische Invariantentheorie . Ergebnisse der Mathematik und ihrer Grenzgebiete , Neue Folge, Band 34 Springer-Verlag, Berlin-New York 1965 vi+145 S. MR 0214602
• Mumford, David; Fogarty, J.; Kirwan, F. Geometrische Invariantentheorie . Dritte Edition. Ergebnisse der Mathematik und ihrer Grenzgebiete (2), 34. Springer-Verlag, Berlin, 1994. xiv+292 S. MR 1304906 ISBN  3-540-56963-4

Frühe Bewerbungen

• Deligne, Pierre ; Mumford, David (1969). "Die Irreduzibilität des Kurvenraums einer gegebenen Gattung" (PDF) . Veröffentlichungen Mathématiques de l'IHÉS . 36 : 75–109. CiteSeerX  10.1.1.589.288 . doi : 10.1007/bf02684599 .
• Faltings, Gerd ; Chai, Ching-Li (1990). Degeneration abelscher Sorten . Ergebnisse der Mathematik und ihrer Grenzgebiete. 22 . Mit einem Anhang von David Mumford. Berlin: Springer-Verlag. doi : 10.1007/978-3-662-02632-8 . ISBN 978-3-540-52015-3. MR  1.083.353 .
• Katz, Nicholas M; Mazur, Barry (1985). Arithmetische Moduli elliptischer Kurven . Annalen der Mathematikstudien. 108 . Princeton University Press . ISBN 978-0-691-08352-0. MR  0.772.569 .

andere Referenzen

• Papadopoulos, Athanase, Hrsg. (2007), Handbuch der Teichmüller-Theorie. vol. I, IRMA Lectures in Mathematics and Theoretical Physics, 11, European Mathematical Society (EMS), Zürich, doi : 10.4171/029 , ISBN  978-3-03719-029-6 , MR 2284826
• Papadopoulos, Athanase, Hrsg. (2009), Handbuch der Teichmüller-Theorie. vol. II, IRMA Lectures in Mathematics and Theoretical Physics, 13, European Mathematical Society (EMS), Zürich, doi : 10.4171/055 , ISBN  978-3-03719-055-5 , MR 2524085
• Papadopoulos, Athanase, Hrsg. (2012), Handbuch der Teichmüller-Theorie. vol. III, IRMA Lectures in Mathematics and Theoretical Physics, 17, European Mathematical Society (EMS), Zürich, doi : 10.4171/103 , ISBN  978-3-03719-103-3 .

Andere Artikel und Quellen

• Harris, Joe ; Morrison, Ian (1998). Moduli von Kurven . Abschlusstexte der Mathematik. 187 . New York: Springer Verlag . doi : 10.1007/b98867 . ISBN 978-0-387-98429-2. MR  1.631.825 .

• Viehweg, Eckart (1995). Quasi-Projektive Moduli für polarisierte Verteiler (PDF) . Springer-Verlag. ISBN 978-3-540-59255-6.

• Simpson, Carlos (1994). "Module der Darstellungen der Fundamentalgruppe einer glatten projektiven Varietät I" (PDF) . Veröffentlichungen Mathématiques de l'IHÉS . 79 : 47–129. doi : 10.1007/bf02698887 .
• Maryam Mirzakhani (2007) "Einfache Geodäten und Weil-Petersson-Volumen von Modulräumen von umrandeten Riemann-Flächen" Inventiones mathematicae

Externe Links

• Lurie, J. (2011). "Moduli Probleme für Ringspektren". Tagungsband des Internationalen Mathematikerkongresses 2010 (ICM 2010) . S. 1099–1125. doi : 10.1142/9789814324359_0088 .