Morleys Trisektorsatz - Morley's trisector theorem

Wenn jeder Scheitelpunktwinkel des äußeren Dreiecks dreiteilig ist, besagt Morleys Trisektorsatz, dass das violette Dreieck gleichseitig ist.

In der ebenen Geometrie , trisector Satzes von Morley , dass Staaten in jedem Dreieck , wobei die drei Schnittpunkte der benachbarten Winkel trisectors ein bilden gleichseitiges Dreieck , das genannte erste Morley Dreieck oder einfach die Morley Dreieck . Der Satz wurde 1899 vom angloamerikanischen Mathematiker Frank Morley entdeckt . Es hat verschiedene Verallgemeinerungen; Insbesondere wenn alle Trisektoren geschnitten sind, erhält man vier weitere gleichseitige Dreiecke.

Beweise

Es gibt viele Beweise für Morleys Theorem, von denen einige sehr technisch sind. Mehrere frühe Beweise basierten auf heiklen trigonometrischen Berechnungen. Zu den jüngsten Beweisen gehören ein algebraischer Beweis von Alain Connes  ( 1998 , 2004 ), der den Satz auf andere allgemeine Felder als die charakteristischen drei erweitert, und John Conways elementarer Geometriebeweis. Letzteres beginnt mit einem gleichseitigen Dreieck und zeigt, dass ein Dreieck darum herum gebaut werden kann , das jedem ausgewählten Dreieck ähnlich ist . Morleys Theorem gilt nicht für sphärische und hyperbolische Geometrie .

Abb. 1: Elementarer Beweis des Morleyschen Trisektorsatzes

Ein Beweis verwendet die trigonometrische Identität

${\ displaystyle \ sin (3 \ theta) = 4 \ sin \ theta \ sin (60 ^ {\ circ} + \ theta) \ sin (120 ^ {\ circ} + \ theta)}$

( 1 )

was unter Verwendung der Summe von zwei Winkeln Identität gezeigt werden kann, um gleich zu sein

${\ displaystyle \ sin (3 \ theta) = - 4 \ sin ^ {3} \ theta +3 \ sin \ theta.}$

Die letzte Gleichung kann überprüft werden, indem die Summe der Identität zweier Winkel zweimal auf die linke Seite angewendet und der Kosinus eliminiert wird.

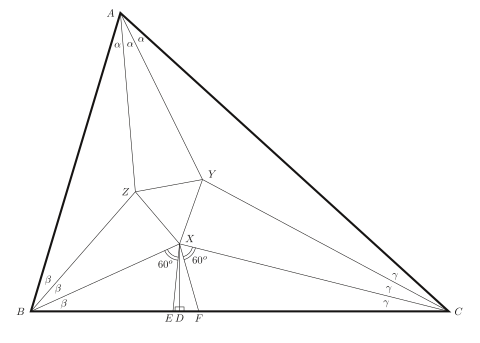
Punkte werden wie gezeigt aufgebaut. Wir haben die Summe von irgendwelchen Winkeln des Dreiecks, so deshalb die Winkel des Dreiecks sind und ${\ displaystyle D, E, F}$${\ displaystyle {\ overline {BC}}}$${\ displaystyle 3 \ alpha +3 \ beta +3 \ gamma = 180 ^ {\ circ}}$${\ displaystyle \ alpha + \ beta + \ gamma = 60 ^ {\ circ}.}$${\ displaystyle XEF}$${\ displaystyle \ alpha, (60 ^ {\ circ} + \ beta),}$${\ displaystyle (60 ^ {\ circ} + \ gamma).}$

Aus der Figur

${\ displaystyle \ sin (60 ^ {\ circ} + \ beta) = {\ frac {\ overline {DX}} {\ overline {XE}}}}$

( 2 )

und

${\ displaystyle \ sin (60 ^ {\ circ} + \ gamma) = {\ frac {\ overline {DX}} {\ overline {XF}}}.}$

( 3 )

Auch aus der Figur

${\ displaystyle \ angle {AYC} = 180 ^ {\ circ} - \ alpha - \ gamma = 120 ^ {\ circ} + \ beta}$

und

${\ displaystyle \ angle {AZB} = 120 ^ {\ circ} + \ gamma.}$

( 4 )

Das Sinusgesetz gilt für Dreiecke und Ausbeuten ${\ displaystyle AYC}$${\ displaystyle AZB}$

${\ displaystyle \ sin (120 ^ {\ circ} + \ beta) = {\ frac {\ overline {AC}} {\ overline {AY}}} \ sin \ gamma}$

( 5 )

und

${\ displaystyle \ sin (120 ^ {\ circ} + \ gamma) = {\ frac {\ overline {AB}} {\ overline {AZ}}} \ sin \ beta.}$

( 6 )

Drücken Sie die Höhe des Dreiecks auf zwei Arten aus ${\ displaystyle ABC}$

${\ displaystyle h = {\ overline {AB}} \ sin (3 \ beta) = {\ overline {AB}} \ cdot 4 \ sin \ beta \ sin (60 ^ {\ circ} + \ beta) \ sin ( 120 ^ {\ circ} + \ beta)}$

und

${\ displaystyle h = {\ overline {AC}} \ sin (3 \ gamma) = {\ overline {AC}} \ cdot 4 \ sin \ gamma \ sin (60 ^ {\ circ} + \ gamma) \ sin ( 120 ^ {\ circ} + \ gamma).}$

wobei Gleichung (1) verwendet wurde, um und in diesen beiden Gleichungen zu ersetzen . Einsetzen der Gleichungen (2) und (5) in die Gleichung und der Gleichungen (3) und (6) in die Gleichung ergibt ${\ displaystyle \ sin (3 \ beta)}$${\ displaystyle \ sin (3 \ gamma)}$${\ displaystyle \ beta}$${\ displaystyle \ gamma}$

${\ displaystyle h = 4 {\ overline {AB}} \ sin \ beta \ cdot {\ frac {\ overline {DX}} {\ overline {XE}}} \ cdot {\ frac {\ overline {AC}} { \ overline {AY}}} \ sin \ gamma}$

und

${\ displaystyle h = 4 {\ overline {AC}} \ sin \ gamma \ cdot {\ frac {\ overline {DX}} {\ overline {XF}}} \ cdot {\ frac {\ overline {AB}} { \ overline {AZ}}} \ sin \ beta}$

Da sind die Zähler gleich

${\ displaystyle {\ overline {XE}} \ cdot {\ overline {AY}} = {\ overline {XF}} \ cdot {\ overline {AZ}}}$

oder

${\ displaystyle {\ frac {\ overline {XE}} {\ overline {XF}}} = {\ frac {\ overline {AZ}} {\ overline {AY}}}.}$

Da Winkel und Winkel gleich sind und die Seiten, die diese Winkel bilden, im gleichen Verhältnis stehen, sind Dreiecke und ähnlich. ${\ displaystyle EXF}$${\ displaystyle ZAY}$${\ displaystyle XEF}$${\ displaystyle AZY}$

Ähnliche Winkel und gleiche und ähnliche Winkel und gleiche Ähnliche Argumente ergeben die Basiswinkel von Dreiecken und ${\ displaystyle AYZ}$${\ displaystyle XFE}$${\ displaystyle (60 ^ {\ circ} + \ gamma)}$${\ displaystyle AZY}$${\ displaystyle XEF}$${\ displaystyle (60 ^ {\ circ} + \ beta).}$${\ displaystyle BXZ}$${\ displaystyle CYX.}$

Insbesondere wird ein Winkel gefunden und aus der Figur sehen wir das ${\ displaystyle BZX}$${\ displaystyle (60 ^ {\ circ} + \ alpha)}$

${\ displaystyle \ angle {AZY} + \ angle {AZB} + \ angle {BZX} + \ angle {XZY} = 360 ^ {\ circ}.}$

Erträge ersetzen

${\ displaystyle (60 ^ {\ circ} + \ beta) + (120 ^ {\ circ} + \ gamma) + (60 ^ {\ circ} + \ alpha) + \ angle {XZY} = 360 ^ {\ circ }}$

wobei Gleichung (4) für den Winkel und daher verwendet wurde ${\ displaystyle AZB}$

${\ displaystyle \ angle {XZY} = 60 ^ {\ circ}.}$

In ähnlicher Weise werden die anderen Winkel des Dreiecks gefunden ${\ displaystyle XYZ}$${\ displaystyle 60 ^ {\ circ}.}$

Seite und Fläche

Das erste Morley-Dreieck hat Seitenlängen

${\ displaystyle a ^ {\ prime} = b ^ {\ prime} = c ^ {\ prime} = 8R \ sin (A / 3) \ sin (B / 3) \ sin (C / 3), \,}$

Dabei ist R der Umfang des ursprünglichen Dreiecks und A, B und C die Winkel des ursprünglichen Dreiecks. Da die Fläche eines gleichseitigen Dreiecks die Fläche des Morleyschen Dreiecks ist, kann ausgedrückt werden als ${\ displaystyle {\ tfrac {\ sqrt {3}} {4}} a '^ {2},}$

${\ displaystyle {\ text {Area}} = 16 {\ sqrt {3}} R ^ {2} \ sin ^ {2} (A / 3) \ sin ^ {2} (B / 3) \ sin ^ { 2} (C / 3).}$

Morleys Dreiecke

Morleys Satz beinhaltet 18 gleichseitige Dreiecke. Das im obigen Trisektorsatz beschriebene Dreieck, das als erstes Morley-Dreieck bezeichnet wird , hat Scheitelpunkte, die in trilinearen Koordinaten relativ zu einem Dreieck ABC wie folgt angegeben sind:

A- Vertex = 1: 2 cos ( C / 3): 2 cos ( B / 3)

B- Vertex = 2 cos ( C / 3): 1: 2 cos ( A / 3)

C- Vertex = 2 cos ( B / 3): 2 cos ( A / 3): 1

Ein weiteres gleichseitiges Dreieck von Morley, das auch ein zentrales Dreieck ist, wird als zweites Morley-Dreieck bezeichnet und ist durch folgende Eckpunkte gegeben:

A- Vertex = 1: 2 cos ( C / 3 - 2π / 3): 2 cos ( B / 3 - 2π / 3)

B- Vertex = 2 cos ( C / 3 - 2π / 3): 1: 2 cos ( A / 3 - 2π / 3)

C- Vertex = 2 cos ( B / 3 - 2π / 3): 2 cos ( A / 3 - 2π / 3): 1

Das dritte von Morleys 18 gleichseitigen Dreiecken, das auch ein zentrales Dreieck ist, wird als drittes Morley-Dreieck bezeichnet und ist durch diese Eckpunkte gegeben:

A- Vertex = 1: 2 cos ( C / 3 - 4π / 3): 2 cos ( B / 3 - 4π / 3)

B- Vertex = 2 cos ( C / 3 - 4π / 3): 1: 2 cos ( A / 3 - 4π / 3)

C- Vertex = 2 cos ( B / 3 - 4π / 3): 2 cos ( A / 3 - 4π / 3): 1

Das erste, zweite und dritte Morley-Dreieck sind paarweise homothetisch . Ein weiteres homothetisches Dreieck wird durch die drei Punkte X auf dem Kreis des Dreiecks ABC gebildet, an denen die Linie XX  ⁻¹ den Kreis tangiert, wobei X  ⁻¹ das isogonale Konjugat von X bezeichnet . Dieses gleichseitige Dreieck, das als Umfangsdreieck bezeichnet wird , hat folgende Eckpunkte:

A- Vertex = csc ( C / 3 - B / 3): csc ( B / 3 + 2 C / 3): -csc ( C / 3 + 2 B / 3)

B- Vertex = -csc ( A / 3 + 2 C / 3): csc ( A / 3 - C / 3): csc ( C / 3 + 2 A / 3)

C- Vertex = csc ( A / 3 + 2 B / 3): - csc ( B / 3 + 2 A / 3): csc ( B / 3 - A / 3)

Ein fünftes gleichseitiges Dreieck, das ebenfalls homothetisch zu den anderen ist, wird erhalten, indem das umlaufende Dreieck π / 6 um seinen Mittelpunkt gedreht wird. Das so genannte zirkumnormale Dreieck hat folgende Eckpunkte:

A- Scheitelpunkt = Sek. ( C / 3 - B / 3): - Sek. ( B / 3 + 2 C / 3): - Sek. ( C / 3 + 2 B / 3)

B- Scheitelpunkt = –sec ( A / 3 + 2 C / 3): sec ( A / 3 - C / 3): –sec ( C / 3 + 2 A / 3)

C- Vertex = –Sek ( A / 3 + 2 B / 3): –Sek ( B / 3 + 2 A / 3): Sek ( B / 3 - A / 3)

Eine Operation namens "Extraversion" kann verwendet werden, um eines der 18 Morley-Dreiecke von einem anderen zu erhalten. Jedes Dreieck kann auf drei verschiedene Arten extravertiert werden. Die 18 Morley-Dreiecke und 27 extravertierten Dreieckspaare bilden die 18 Eckpunkte und 27 Kanten des Pappus-Diagramms .

Verwandte Dreieckszentren

Der Schwerpunkt des ersten Morley-Dreiecks wird in trilinearen Koordinaten durch angegeben

Morley-Zentrum = X (356) = cos ( A / 3) + 2 cos ( B / 3) cos ( C / 3): cos ( B / 3) + 2 cos ( C / 3) cos ( A / 3): cos ( C / 3) + 2 cos ( A / 3) cos ( B / 3).

Das erste Morley-Dreieck ist Perspektive zu Dreieck ABC : Die Linien, die jeweils einen Scheitelpunkt des ursprünglichen Dreiecks mit dem gegenüberliegenden Scheitelpunkt des Morley-Dreiecks verbinden, stimmen am Punkt überein

1. Morley-Taylor-Marr-Zentrum = X (357) = Sek. ( A / 3): Sek. ( B / 3): Sek. ( C / 3).

Siehe auch

• Winkeltrisektion
• Hofstadter Punkte
• Morley-Zentren

Anmerkungen

Verweise

• Connes, Alain (1998), "Ein neuer Beweis von Morleys Theorem" , Publications Mathématiques de l'IHÉS , S88 : 43–46 .
• Connes, Alain (Dezember 2004), "Symmetries" (PDF) , Newsletter der European Mathematical Society , 54 .
• Coxeter, HSM ; Greitzer, SL (1967), Geometry Revisited , Mathematische Vereinigung von Amerika , LCCN   67-20607
• Francis, Richard L. (2002), "Moderne mathematische Meilensteine: Morleys Geheimnis" (PDF) , Missouri Journal of Mathematical Sciences , 14 (1), doi : 10.35834 / 2002/1401016 .
• Guy, Richard K. (2007), "The Lighthouse Theorem, Morley & Malfatti - ein Budget der Paradoxien" (PDF) , American Mathematical Monthly , 114 (2): 97–141, doi : 10.1080 / 00029890.2007.11920398 , JSTOR   27642143 , MR   2290364 , archiviert vom Original (PDF) am 01.04.2010 .
• Oakley, CO; Baker, JC (1978), "The Morley Trisector Theorem", American Mathematical Monthly , 85 (9): 737–745, doi : 10.2307 / 2321680 , JSTOR   2321680 .
• Taylor, F. Glanville; Marr, WL (1913–14), "Die sechs Trisektoren jedes Winkels eines Dreiecks", Proceedings of the Edinburgh Mathematical Society , 33 : 119–131, doi : 10.1017 / S0013091500035100 .

Externe Links

• Morleys Theorem bei MathWorld
• Morleys Trisektionssatz bei MathPages
• Morleys Theorem von Oleksandr Pavlyk, The Wolfram Demonstrations Project .