Regelmäßiges 4-Polytop - Regular 4-polytope

Der Tesserakt ist einer von 6 konvexen regelmäßigen 4-Polytopen

In der Mathematik ist ein reguläres 4-Polytop ein reguläres vierdimensionales Polytop . Sie sind die vierdimensionalen Analoga der regelmäßigen Polyeder in drei Dimensionen und der regelmäßigen Vielecke in zwei Dimensionen.

Es gibt sechs konvexe und zehn sternförmige regelmäßige 4-Polytope, was insgesamt sechzehn ergibt.

Geschichte

Die konvexen regelmäßigen 4-Polytope wurden erstmals Mitte des 19. Jahrhunderts von dem Schweizer Mathematiker Ludwig Schläfli beschrieben . Er entdeckte, dass es genau sechs solcher Figuren gibt.

Schläfli fand auch vier der regulären Stern-4-Polytope: die großen 120-Zellen , die großen Sternchen 120 , die großen 600-Zellen und die großen großen Sternchen 120-Zellen . Er übersprang die verbleibenden sechs, weil er keine Formen zulassen würde, die die Euler-Eigenschaft auf Zellen oder Scheitelpunktfiguren nicht erfüllten (für Null-Loch-Tori: F  −  E  +  V  = 2). Davon ausgenommen sind Zellen und Vertexfiguren wie das große Dodekaeder {5,5/2} und kleines sternförmiges Dodekaeder {5/2,5}.

Edmund Hess (1843–1903) veröffentlichte die vollständige Liste in seinem 1883 erschienenen deutschen Buch Einleitung in die Lehre von der Kugelteilung mit besonderer Berücksichtigung ihrer Anwendung auf die Theorie der Gleichflächigen und der gleicheckigen Polyeder .

Konstruktion

Die Existenz eines regelmäßigen 4-Polytop wird durch die Existenz des regelmäßigen Polyeder beschränkt , die ihre Zellen und eine Form Diederwinkel constraint ${\displaystyle \{p,q,r\}}$${\displaystyle \{p,q\},\{q,r\}}$

${\displaystyle \sin {\frac {\pi }{p}}\sin {\frac {\pi }{r}}<\cos {\frac {\pi }{q}}}$

um sicherzustellen, dass sich die Zellen zu einer geschlossenen 3-Fläche treffen.

Die beschriebenen sechs konvexen und zehn sternförmigen Polytope sind die einzigen Lösungen für diese Beschränkungen.

Es gibt vier nichtkonvexe Schläfli-Symbole {p,q,r}, die gültige Zellen {p,q} und Vertexfiguren {q,r} haben und den Diedertest bestehen, aber keine endlichen Figuren erzeugen: {3,5/2,3}, {4,3,5/2}, { 5/2,3,4}, { 5/2,3,5/2}.

Regelmäßige konvexe 4-Polytope

Die regelmäßig konvexen 4-Polytope sind die vierdimensionalen Analoga der platonischen Körper in drei Dimensionen und der konvexen regelmäßigen Polygone in zwei Dimensionen.

Fünf der sechs sind eindeutig Analoga der fünf entsprechenden platonischen Körper. Die sechste, die 24-Zellen , hat kein reguläres Analogon in drei Dimensionen. Es gibt jedoch ein Paar unregelmäßiger Körper, das Kuboktaeder und sein duales das rhombische Dodekaeder , die teilweise Analoga zu den 24-Zellen sind (in komplementärer Weise). Zusammen können sie als das dreidimensionale Analogon der 24-Zelle angesehen werden.

Jedes konvexe regelmäßige 4-Polytop wird von einer Menge dreidimensionaler Zellen begrenzt, die alle platonische Körper des gleichen Typs und der gleichen Größe sind. Diese werden entlang ihrer jeweiligen Gesichter in regelmäßiger Weise zusammengefügt.

Eigenschaften

Wie ihre dreidimensionalen Analoga können die konvexen regelmäßigen 4-Polytope natürlich nach Größe als Maß für den 4-dimensionalen Inhalt (Hypervolumen) für den gleichen Radius geordnet werden. Jedes größere Polytop in der Sequenz ist runder als sein Vorgänger und umschließt mehr Inhalt innerhalb des gleichen Radius. Der 4-Simplex (5-Zellen) ist der kleinste Grenzfall, und der 120-Zellen ist der größte. Die Komplexität (gemessen durch den Vergleich von Konfigurationsmatrizen oder einfach der Anzahl der Scheitelpunkte) folgt der gleichen Reihenfolge.

Regelmäßige konvexe 4-Polytope
Symmetriegruppe	Ein 4	B 4		F 4	H 4
Name	5-Zellen Hyper- Tetraeders	16-Zellen Hyper- Oktaeder	8-Zellen Hyper- Würfel	24-Zellen	600-Zellen Hyper- Ikosaeder	120-Zellen Hyper- Dodekaeder
Schläfli-Symbol	{3, 3, 3}	{3, 3, 4}	{4, 3, 3}	{3, 4, 3}	{3, 3, 5}	{5, 3, 3}
Coxeter-Diagramm
Graph
Scheitelpunkte	5	8	16	24	120	600
Kanten	10	24	32	96	720	1200
Gesichter	10 Dreiecke	32 Dreiecke	24 Quadrate	96 Dreiecke	1200 Dreiecke	720 Fünfecke
Zellen	5 Tetraeder	16 Tetraeder	8 Würfel	24 Oktaeder	600 Tetraeder	120 Dodekaeder
Großer Radius	1	1	1	1	1	1
Kantenlänge	√ 5/√ 2 1,581	√ 2 ≈ 1,414	1	1	1/φ 0,618	1/√ 2 φ 2 0,270
Kurzer Radius	1/4	1/2	1/2	√ 2/2 0,707	1 - (√ 2/2 √ 3 φ) 2 0,936	1 - (1/2 √ 3 φ) 2 0,968
Bereich	10•√ 8/3 9,428	32•√ 3/4 13.856	24	96•√ 3/4 41.569	1200•√ 3/8φ 2 99.238	720•25+10 √ 5/8φ 4 621,9
Volumen	5•5 √ 5/24 2.329	16•1/3 5.333	8	24•√ 2/3 11.314	600•1/3 √ 8 φ 3 16.693	120•2 +/2 √ 8 φ 3 18.118
4-Inhalt	√ 5/24•(√ 5/2) 4 ≈ 0,146	2/3 0,667	1	2	KurzVol/4 3.907	KurzVol/4 4.385

Die folgende Tabelle listet einige Eigenschaften der sechs konvexen regulären 4-Polytope auf. Die Symmetriegruppen dieser 4-Polytope sind alle Coxeter-Gruppen und in der in diesem Artikel beschriebenen Notation angegeben. Die Zahl hinter dem Namen der Gruppe ist die Reihenfolge der Gruppe.

Namen	Bild	Familie	Schläfli Coxeter	V	E	F	C	Vert. Feige.	Dual	Symmetriegruppe
5-zelliges Pentachoron Pentatop 4-Simplex		n- simplex (Eine n- Familie)	{3,3,3}	5	10	10 {3}	5 {3,3}	{3,3}	selbst-dual	A 4 [3,3,3]	120
16-Zellen- Hexadecachoron- 4-Orthoplex		n- Orthoplex (B n -Familie)	{3,3,4}	8	24	32 {3}	16 {3,3}	{3,4}	8-Zellen	B 4 [4,3,3]	384
8-zelliger Oktachoron- Tesseract 4-Würfel		Hyperwürfel n -Würfel (B n Familie)	{4,3,3}	16	32	24 {4}	8 {4,3}	{3,3}	16-Zellen
24-Zelle icositetrachoron Octaplex polyoctahedron (pO)		F n Familie	{3,4,3}	24	96	96 {3}	24 {3,4}	{4,3}	selbst-dual	F 4 [3,4,3]	1152
600- zelliges Hexacosichoron- Tetraplex- Polytetraeder (pT)		n-pentagonales Polytop (H n -Familie)	{3,3,5}	120	720	1200 {3}	600 {3,3}	{3,5}	120-Zellen	H 4 [5,3,3]	14400
120-Zellen Hecatonicosachoron dodecacontachoron dodecaplex polydodecahedron (pD)		n-pentagonales Polytop (H n -Familie)	{5,3,3}	600	1200	720 {5}	120 {5,3}	{3,3}	600-Zellen

John Conway befürwortete die Namen Simplex, Orthoplex, Tesseract, Octaplex oder Polyoctahedron (pO), Tetraplex oder Polytetraeder (pT) und Dodecaplex oder Polydodecaedron (pD).

Norman Johnson befürwortete die Namen n-Zelle oder Pentachoron, Hexadecachoron, Tesserakt oder Oktachoron, Ikositetrachoron, Hexacosichoron und Hecatonicosachoron (oder Dodecacontachoron) und prägte den Begriff Polychoron als 4D-Analogie zum 3D-Polyeder und 2D-Polygon, ausgedrückt aus dem Griechischen root poly ("viele") und choros ("room" oder "space").

Die Euler-Charakteristik für alle 4-Polytope ist null, wir haben das 4-dimensionale Analogon der polyedrischen Formel von Euler:

${\displaystyle N_{0}-N_{1}+N_{2}-N_{3}=0\,}$

wobei N _k die Anzahl der k- Flächen im Polytop bezeichnet (eine Ecke ist eine 0-Fläche, eine Kante ist eine 1-Fläche usw.).

Die Topologie eines gegebenen 4-Polytops wird durch seine Betti-Zahlen und Torsionskoeffizienten definiert .

Als Konfigurationen

Ein reguläres 4-Polytop kann vollständig als Konfigurationsmatrix beschrieben werden, die die Anzahl seiner Komponentenelemente enthält. Die Zeilen und Spalten entsprechen Scheitelpunkten, Kanten, Flächen und Zellen. Die diagonalen Zahlen (von links oben nach rechts unten) geben an, wie viele von jedem Element im gesamten 4-Polytop vorkommen. Die nicht diagonalen Zahlen geben an, wie viele Elemente der Spalte im oder am Element der Zeile vorkommen. Zum Beispiel gibt es 2 Scheitelpunkte in jeder Kante (jede Kante hat 2 Scheitelpunkte) und 2 Zellen treffen auf jeder Seite (jede Seite gehört zu 2 Zellen) in jedem regulären 4-Polytop. Beachten Sie, dass die Konfiguration für das duale Polytop durch Drehen der Matrix um 180 Grad erhalten werden kann.

5-Zellen {3,3,3}	16-Zellen- {3,3,4}	Tesserakt {4,3,3}	24-Zellen {3,4,3}	600-Zellen {3,3,5}	120-Zellen {5,3,3}
${\displaystyle {\begin{bmatrix}{\begin{matrix}5&4&6&4\\2&10&3&3\\3&3&10&2\\4&6&4&5\end{matrix}}\end{bmatrix}}}$	${\displaystyle {\begin{bmatrix}{\begin{matrix}8&6&12&8\\2&24&4&4\\3&3&32&2\\4&6&4&16\end{matrix}}\end{bmatrix}}}$	${\displaystyle {\begin{bmatrix}{\begin{matrix}16&4&6&4\\2&32&3&3\\4&4&24&2\\8&12&6&8\end{matrix}}\end{bmatrix}}}$	${\displaystyle {\begin{bmatrix}{\begin{matrix}24&8&12&6\\2&96&3&3\\3&3&96&2\\6&12&8&24\end{matrix}}\end{bmatrix}}}$	${\displaystyle {\begin{bmatrix}{\begin{matrix}120&12&30&20\\2&720&5&5\\3&3&1200&2\\4&6&4&600\end{matrix}}\end{bmatrix}}}$	${\displaystyle {\begin{bmatrix}{\begin{matrix}600&4&6&4\\2&1200&3&3\\5&5&720&2\\20&30&12&120\end{matrix}}\end{bmatrix}}}$

Visualisierung

Die folgende Tabelle zeigt einige 2-dimensionale Projektionen dieser 4-Polytope. Verschiedene andere Visualisierungen finden Sie in den externen Links unten. Die Graphen des Coxeter-Dynkin-Diagramms sind auch unterhalb des Schläfli-Symbols angegeben .

A 4 = [3,3,3]	B 4 = [4,3,3]		F 4 = [3,4,3]	H 4 = [5,3,3]
5-Zellen	16-Zellen	8-Zellen	24-Zellen	600-Zellen	120-Zellen
{3,3,3}	{3,3,4}	{4,3,3}	{3,4,3}	{3,3,5}	{5,3,3}
Solide orthografische 3D- Projektionen
Tetraedrischen Hülle (Zelle / Vertex-zentriert)	Kubische Hülle (zellzentriert)	Kubische Hülle (zellzentriert)	Kuboktaedrische Hülle ( zellzentriert )	Pentakis icosidodekaedrische Hülle (scheitelzentriert)	Abgeschnittene rhombische Triacontaeder- Hülle (zellzentriert)
Drahtgitter- Schlegel-Diagramme ( Perspektivische Projektion )
Zellzentriert	Zellzentriert	Zellzentriert	Zellzentriert	Scheitelpunktzentriert	Zellzentriert
Stereografische Projektionen mit Drahtgitter ( 3-Sphäre )

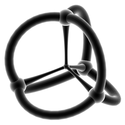
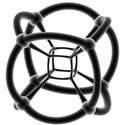
Regulärer Stern (Schläfli–Hess) 4-Polytope

Dies zeigt die Beziehungen zwischen den vierdimensionalen Sternenpolytopen. Die 2 konvexen Formen und 10 Sternenformen sind in 3D als Eckpunkte eines Kuboktaeders zu sehen .

Eine Teilmenge von Beziehungen zwischen 8 Formen aus dem 120-Zellen-Polydodekaeder (pD). Die drei Operationen {a,g,s} sind kommutierbar und definieren ein kubisches Gerüst. Bei vertikaler Positionierung sind 7 Dichten zu sehen, wobei 2 duale Formen die gleiche Dichte aufweisen.

Die Schläfli-Hess 4-Polytope sind der komplette Satz von 10 regelmäßigen sich selbst schneidenden Sternpolychoren ( vierdimensionale Polytope ). Sie sind nach ihren Entdeckern benannt: Ludwig Schläfli und Edmund Hess . Jedes wird durch ein Schläfli-Symbol { p , q , r } dargestellt, in dem eine der Zahlen5/2. Sie sind somit analog zu den regelmäßigen nichtkonvexen Kepler-Poinsot-Polyedern , die wiederum analog zum Pentagramm sind.

Namen

Ihre hier angegebenen Namen wurden von John Conway gegeben , der Cayleys Namen für die Kepler-Poinsot-Polyeder erweitert : Zusammen mit Stern und Groß fügt er einen großen Modifikator hinzu. Conway bot diese Betriebsdefinitionen an:

1. stellation – ersetzt Kanten durch längere Kanten in gleichen Zeilen. (Beispiel: ein Fünfeck stelliert sich zu einem Pentagramm )
2. Vergrößerung – ersetzt die Gesichter durch große in den gleichen Ebenen. (Beispiel: ein Ikosaeder vergrößert sich zu einem großen Ikosaeder )
3. Vergrößerung – ersetzt die Zellen durch große in den gleichen 3-Räumen. (Beispiel: eine 600-Zelle vergrößert sich zu einer großen 600-Zelle )

John Conway benennt die 10 Formen aus 3 regelmäßigzelligen 4-Polytopen: pT=Polytetraeder {3,3,5} (eine tetraedrische 600-Zelle ), pI=Polyicoshedron {3,5,5/2} (eine ikosaedrische 120-Zelle ) und pD=Polydodekaeder {5,3,3} (eine dodekaedrische 120-Zelle ), mit Präfix-Modifikatoren: g , a und s für groß, (ag)groß und stelliert. Die letzte Stellation, das große sternförmige Polydodekaeder, enthält sie alle als keuchend .

Symmetrie

Alle zehn Polychora haben [3,3,5] ( H ₄ ) hexacosichorische Symmetrie . Sie werden aus 6 verwandten Goursat-Tetraeder -Symmetriegruppen rationaler Ordnung erzeugt : [3,5,5/2], [5,5/2,5], [5,3,5/2], [5/2,5 ,5/2], [5,5/2,3] und [3,3,5/2].

Jede Gruppe hat 2 reguläre Star-Polychora, mit Ausnahme von zwei Gruppen, die selbst-dual sind und nur eine haben. Es gibt also 4 Dual-Paare und 2 Self-Dual-Formen unter den zehn regulären Sternpolychoren.

Eigenschaften

Notiz:

• Es gibt 2 einzigartige Vertex-Anordnungen , die denen der 120-Zellen und 600-Zellen entsprechen .
• Es gibt 4 einzigartige Kantenanordnungen , die als orthografische Projektionen von Drahtmodellen dargestellt werden .
• Es gibt 7 einzigartige Flächenanordnungen , die als feste (gesichtsfarbene) orthografische Projektionen angezeigt werden .

Die Zellen (Polyeder), ihre Flächen (Polygone), die polygonalen Kantenfiguren und polyedrischen Scheitelfiguren werden durch ihre Schläfli-Symbole identifiziert .

Name Conway (Abkürzung)	Orthogonale Projektion	Schläfli Coxeter	C {p, q}	F {p}	E {r}	V {q, r}	Höhlen.	χ
Ikosaedrisches 120-Zellen- Polyikosaeder (pI)		{3,5,5/2}	120 {3,5}	1200 {3}	720 {5/2 }	120 {5,5/2}	4	480
Kleines stelliertes 120- zelliges stelliertes Polydodekaeder (spD)		{5/2,5,3}	120 {5/2,5}	720 {5/2}	1200 {3}	120 {5,3}	4	−480
Großes 120-Zellen großes Polydodekaeder (gpD)		{5,5/2,5}	120 {5,5/2}	720 {5}	720 {5}	120 {5/2,5}	6	0
Großes 120-Zellen- großes Polydodekaeder (apD)		{5,3,5/2}	120 {5,3}	720 {5}	720 {5/2}	120 {3,5/2}	20	0
Großes sternförmiges 120- zelliges großes sternförmiges Polydodekaeder (gspD)		{5/2,3,5}	120 {5/2,3}	720 {5/2}	720 {5}	120 {3,5}	20	0
Grand stellated 120-cell Grand stellated Polydodekaeder (aspD)		{5/2,5,5/2}	120 {5/2,5}	720 {5/2}	720 {5/2}	120 {5,5/2}	66	0
Urgroßes Urgroßpolydodekaeder mit 120 Zellen (gapD)		{5,5/2,3}	120 {5,5/2}	720 {5}	1200 {3}	120 {5/2,3}	76	−480
Großes Ikosaeder 120-Zellen großes Polyikosaeder (gpI)		{3,5/2,5}	120 {3,5/2}	1200 {3}	720 {5}	120 {5/2,5}	76	480
Großes 600-Zellen- Grand-Polytetraeder (apT)		{3,3,5/2}	600 {3,3}	1200 {3}	720 {5/2}	120 {3,5/2}	191	0
Great Grand stellated 120-Zellen- Great Grand stellated Polydodekaeder (gaspD)		{5/2,3,3}	120 {5/2,3}	720 {5/2}	1200 {3}	600 {3,3}	191	0

Siehe auch

• Regelmäßiges Polytop
• Liste der regelmäßigen Polytope
• Unendlich regelmäßige 4-Polytope:
  • Eine normale euklidische Wabe: {4,3,4}
  • Vier kompakte regelmäßige hyperbolische Waben: {3,5,3}, {4,3,5}, {5,3,4}, {5,3,5}
  • Elf parakompakte regelmäßige hyperbolische Waben: {3,3,6}, {6,3,3}, {3,4,4}, {4,4,3}, {3,6,3}, {4,3 ,6}, {6,3,4}, {4,4,4}, {5,3,6}, {6,3,5} und {6,3,6}.
• Abstrakte regelmäßige 4-Polytope:
  • 11-Zellen {3,5,3}
  • 57-Zellen {5,3,5}
• Einheitliche 4-Polytope Einheitliche 4-Polytop-Familien, die aus diesen 6 regulären Formen aufgebaut sind.
• Platonischer Körper
• Kepler-Poinsot-Polyeder — reguläres Sternpolyeder
• Stern - Polygon - regelmäßiger Stern Polygone
• 4-Polytop
• 5-Polytop
• 6-Polytop

Verweise

Zitate

Literaturverzeichnis

Externe Links

• Weisstein, Eric W. "Reguläres Polychoron" . MathWorld .
• Jonathan Bowers, 16 regelmäßige 4-Polytope
• Reguläre 4D Polytope Foldouts
• Katalog der Polytopbilder Eine Sammlung stereographischer Projektionen von 4-Polytopen.
• Ein Katalog einheitlicher Polytope
• Dimensionen 2-stündiger Film über die vierte Dimension (enthält stereografische Projektionen aller regulären 4-Polytope)
• Olschewski, Georg. "Hekatonicosachoron" . Glossar für Hyperraum . Archiviert vom Original am 4. Februar 2007.
  • Olschewski, Georg. "Hexacosichoron" . Glossar für Hyperraum . Archiviert vom Original am 4. Februar 2007.
  • Olschewski, Georg. "Stellung" . Glossar für Hyperraum . Archiviert vom Original am 4. Februar 2007.
  • Olschewski, Georg. "Erhöhung" . Glossar für Hyperraum . Archiviert vom Original am 4. Februar 2007.
  • Olschewski, Georg. "Ergänzung" . Glossar für Hyperraum . Archiviert vom Original am 4. Februar 2007.
• Reguläres Polytop
• Die regelmäßige Stern-Polychora
• Hypersolids