Taylors Satz - Taylor's theorem

Die Exponentialfunktion y  =  e ^x (rot) und das entsprechende Taylor-Polynom vom Grad vier (grün gestrichelt) um den Ursprung.

In der Analysis gibt der Satz von Taylor eine Approximation einer k- mal differenzierbaren Funktion um einen gegebenen Punkt durch ein Polynom vom Grad k , das als Taylor-Polynom k- ter Ordnung bezeichnet wird . Für eine glatte Funktion ist das Taylor-Polynom die Trunkierung an der Ordnung k der Taylor-Reihe der Funktion. Das Taylor-Polynom erster Ordnung ist die lineare Approximation der Funktion, und das Taylor-Polynom zweiter Ordnung wird oft als quadratische Approximation bezeichnet . Es gibt mehrere Versionen des Satzes von Taylor, von denen einige explizite Schätzungen des Approximationsfehlers der Funktion durch ihr Taylor-Polynom liefern.

Taylors Theorem ist nach dem Mathematiker Brook Taylor benannt , der 1715 eine Version davon angab, obwohl eine frühere Version des Ergebnisses bereits 1671 von James Gregory erwähnt wurde .

Der Satz von Taylor wird in Einführungskursen in die Analysis gelehrt und ist eines der zentralen elementaren Werkzeuge der mathematischen Analysis . Es liefert einfache arithmetische Formeln, um die Werte vieler transzendenter Funktionen wie der Exponentialfunktion und trigonometrischen Funktionen genau zu berechnen . Es ist der Ausgangspunkt für das Studium analytischer Funktionen und ist grundlegend in verschiedenen Bereichen der Mathematik sowie in der numerischen Analysis und der mathematischen Physik . Der Satz von Taylor lässt sich auch auf multivariate und vektorwertige Funktionen verallgemeinern .

Motivation

Graph von f ( x ) = e ^x (blau) mit seiner linearen Näherung P ₁ ( x ) = 1 + x (rot) bei a  = 0.

Wenn eine reellwertige Funktion f ( x ) im Punkt x = a differenzierbar ist , dann hat sie in der Nähe dieses Punktes eine lineare Näherung . Das heißt, es gibt eine Funktion h ₁ ( x ) mit

${\displaystyle f(x)=f(a)+f'(a)(xa)+h_{1}(x)(xa),\quad \lim_{x\to a}h_{1}(x )=0.}$

Hier

${\displaystyle P_{1}(x)=f(a)+f'(a)(xa)}$

ist die lineare Approximation von f ( x ) für x in der Nähe des Punktes a , dessen Graph y = P ₁ ( x ) die Tangente an den Graphen y = f ( x ) bei x = a ist . Der Fehler in der Näherung ist:

${\displaystyle R_{1}(x)=f(x)-P_{1}(x)=h_{1}(x)(xa).}$

Da x zu a tendiert  , geht dieser Fehler viel schneller auf Null als , was eine nützliche Näherung ergibt. ${\displaystyle f'(a)(x{-}a)}$${\displaystyle f(x)\approx P_{1}(x)}$

Graph von f ( x ) = e ^x (blau) mit seiner quadratischen Näherung P ₂ ( x ) = 1 + x + x ² /2 (rot) bei a  = 0. Man beachte die Verbesserung der Näherung.

Für eine bessere Annäherung an f ( x ) können wir anstelle einer linearen Funktion ein quadratisches Polynom anpassen:

${\displaystyle P_{2}(x)=f(a)+f'(a)(xa)+{\frac {f''(a)}{2}}(xa)^{2}.}$

Anstatt nur eine Ableitung von f ( x ) bei x = a abzugleichen, hat dieses Polynom die gleichen ersten und zweiten Ableitungen, wie sich bei der Differenzierung zeigt.

Der Satz von Taylor stellt sicher, dass die quadratische Näherung in einer hinreichend kleinen Umgebung von x = a genauer ist als die lineare Näherung. Speziell,

${\displaystyle f(x)=P_{2}(x)+h_{2}(x)(xa)^{2},\quad \lim_{x\to a}h_{2}(x)= 0.}$

Hier ist der Fehler in der Näherung

${\displaystyle R_{2}(x)=f(x)-P_{2}(x)=h_{2}(x)(xa)^{2},}$

die, angesichts des begrenzenden Verhaltens von , schneller gegen Null geht, als wenn x gegen a strebt  . ${\displaystyle h_{2}}$${\displaystyle (xa)^{2}}$

Approximation von f ( x ) = 1/(1 +  x ² ) (blau) durch seine Taylor-Polynome P _k der Ordnung k  = 1, …, 16 zentriert bei x  = 0 (rot) und x  = 1 (grün). Außerhalb von (−1, 1) bzw. (1 − √2, 1 + √2) verbessern sich die Näherungen überhaupt nicht.

Ebenso könnten wir noch bessere Näherungen an f erhalten, wenn wir Polynome höheren Grades verwenden, da wir dann noch mehr Ableitungen mit f am gewählten Basispunkt abgleichen können.

In der Regel ist der Fehler eine Funktion durch ein Polynom vom Grad bei der Angleichung k wird als Null viel schneller gehen als x zu neigt  ein . Es gibt jedoch auch unendlich differenzierbare Funktionen, bei denen eine Erhöhung des Grades des Näherungspolynoms die Näherungsgenauigkeit nicht erhöht: Wir sagen, eine solche Funktion ist bei x = a nicht analytisch : sie ist nicht (lokal) bestimmt durch seine Ableitungen an dieser Stelle. ${\displaystyle (xa)^{k}}$

Der Satz von Taylor ist asymptotischer Natur: Er sagt uns nur, dass der Fehler R _k in einer Näherung durch ein Taylor-Polynom k- ter Ordnung P _k schneller gegen null tendiert als jedes von null verschiedene Polynom k- ten Grades als x  →  a . Es sagt uns nicht, wie groß der Fehler in einer konkreten Umgebung des Expansionszentrums ist, aber zu diesem Zweck gibt es explizite Formeln für den Restterm (siehe unten), die unter einigen zusätzlichen Regularitätsannahmen für f gültig sind . Diese verbesserten Versionen des Satzes von Taylor führen typischerweise zu einheitlichen Schätzungen für den Näherungsfehler in einer kleinen Umgebung des Zentrums der Expansion, aber die Schätzungen nicht unbedingt für Nachbarschaften halten , die zu groß sind, auch wenn die Funktion f ist analytisch . In dieser Situation muss man möglicherweise mehrere Taylor-Polynome mit unterschiedlichen Entwicklungszentren auswählen, um zuverlässige Taylor-Approximationen der Originalfunktion zu erhalten (siehe Animation rechts).

Es gibt mehrere Möglichkeiten, den Restterm zu verwenden:

1. Schätzen Sie den Fehler für ein Polynom P _k ( x ) vom Grad k ab, indem Sie f ( x ) in einem gegebenen Intervall ( a – r , a + r ) schätzen . (Angesichts des Intervalls und des Grads finden wir den Fehler.)
2. Finden Sie den kleinsten Grad k, für den das Polynom P _k ( x ) f ( x ) innerhalb einer gegebenen Fehlertoleranz in einem gegebenen Intervall ( a − r , a + r ) annähert . (Angesichts des Intervalls und der Fehlertoleranz finden wir den Grad.)
3. Finden Sie das größte Intervall ( a − r , a + r ), auf dem sich P _k ( x ) innerhalb einer gegebenen Fehlertoleranz an f ( x ) annähert. (Angesichts des Grades und der Fehlertoleranz finden wir das Intervall.)

Satz von Taylor in einer reellen Variablen

Aussage des Theorems

Die genaue Aussage der grundlegendsten Version des Satzes von Taylor lautet wie folgt:

Das im Satz von Taylor vorkommende Polynom ist das Taylor-Polynom k- ter Ordnung

${\displaystyle P_{k}(x)=f(a)+f'(a)(xa)+{\frac {f''(a)}{2!}}(xa)^{2}+\ cdots +{\frac {f^{(k)}(a)}{k!}}(xa)^{k}}$

der Funktion f im Punkt a . Das Taylor-Polynom ist das eindeutige "asymptotisch am besten passende" Polynom in dem Sinne, dass wenn es eine Funktion h _k  : R → R und ein Polynom k- ter Ordnung p gibt, so dass

${\displaystyle f(x)=p(x)+h_{k}(x)(xa)^{k},\quad\lim_{x\to a}h_{k}(x)=0,}$

dann p  =  P _k . Der Satz von Taylor beschreibt das asymptotische Verhalten des Restterms

${\displaystyle R_{k}(x)=f(x)-P_{k}(x),}$

das ist der Approximationsfehler bei der Approximation von f mit seinem Taylor-Polynom. In der Notation Little-o lautet die Aussage im Satz von Taylor wie folgt:

${\displaystyle R_{k}(x)=o(|xa|^{k}),\quad x\to a.}$

Explizite Formeln für den Rest

Unter stärkeren Regularitätsannahmen für f gibt es mehrere präzise Formeln für den Restterm R _k des Taylor-Polynoms, von denen die gebräuchlichsten die folgenden sind.

Diese Verfeinerungen des Satzes von Taylor werden normalerweise mit dem Mittelwertsatz bewiesen , daher der Name. Auch andere ähnliche Ausdrücke können gefunden werden. Wenn beispielsweise G ( t ) auf dem geschlossenen Intervall stetig und mit einer nicht verschwindenden Ableitung auf dem offenen Intervall zwischen a und x differenzierbar ist , dann

${\displaystyle R_{k}(x)={\frac {f^{(k+1)}(\xi)}{k!}}(x-\xi)^{k}{\frac {G( x)-G(a)}{G'(\xi)}}}$

für eine Zahl ξ zwischen a und x . Diese Version deckt die Lagrange- und Cauchy-Formen des Rests als Spezialfälle ab und wird im Folgenden mit dem Mittelwertsatz von Cauchy bewiesen .

Die Aussage für die Integralform des Rests ist weiter fortgeschritten als die vorherigen und erfordert ein Verständnis der Lebesgue-Integrationstheorie für die volle Allgemeinheit. Sie gilt aber auch im Sinne des Riemann-Integrals, sofern die ( k  + 1)-te Ableitung von f auf dem abgeschlossenen Intervall [ a , x ] stetig ist .

Wegen der absoluten Stetigkeit von f ^{( k )} auf dem abgeschlossenen Intervall zwischen a und x existiert seine Ableitung f ^{( k +1)} als L ¹ -Funktion, und das Ergebnis kann durch eine formale Rechnung unter Verwendung des Fundamentalsatzes der Infinitesimalrechnung und bewiesen werden Integration nach Teilen .

Schätzungen für den Rest

In der Praxis ist es oft nützlich, den in der Taylor-Approximation auftretenden Restterm abschätzen zu können, anstatt eine exakte Formel dafür zu haben. Angenommen, f ist ( k + 1) -mal stetig differenzierbar in einem Intervall I mit a . Angenommen, es gibt reelle Konstanten q und Q mit

${\displaystyle q\leq f^{(k+1)}(x)\leq Q}$

während ich . Dann erfüllt der Restterm die Ungleichung

${\displaystyle q{\frac {(xa)^{k+1}}{(k+1)!}}\leq R_{k}(x)\leq Q{\frac {(xa)^{k+ 1}}{(k+1)!}},}$

wenn x > a , und eine ähnliche Schätzung, wenn x < a . Dies ist eine einfache Folge der Lagrange-Form des Rests. Insbesondere wenn

${\displaystyle |f^{(k+1)}(x)|\leq M}$

auf einem Intervall I = ( a − r , a + r ) mit einigen , dann ${\displaystyle r>0}$

${\displaystyle |R_{k}(x)|\leq M{\frac {|xa|^{k+1}}{(k+1)!}}\leq M{\frac {r^{k+ 1}}{(k+1)!}}}$

für alle x ∈( a − r , a + r ). Die zweite Ungleichung wird als einheitliche Schätzung bezeichnet , weil sie für alle x auf dem Intervall ( a − r , a + r ) einheitlich gilt .

Beispiel

Approximation von e ^x (blau) durch seine Taylor-Polynome P _k der Ordnung k  = 1,…,7 zentriert bei x  = 0 (rot).

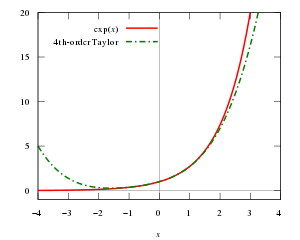
Angenommen, wir möchten den Näherungswert der Funktion f ( x ) = e ^x auf dem Intervall [−1,1] finden und dabei sicherstellen, dass der Näherungsfehler nicht mehr als 10 ⁻⁵ beträgt . In diesem Beispiel geben wir vor, dass wir nur die folgenden Eigenschaften der Exponentialfunktion kennen:

${\displaystyle e^{0}=1,\qquad {\frac {d}{dx}}e^{x}=e^{x},\qquad e^{x}>0,\qquad x\in \mathbb{R}.}$

( ⁎ )

Aus diesen Eigenschaften folgt f ^{( k )} ( x ) = e ^x für alle k , insbesondere f ^{( k )} (0) = 1 . Somit sind das Taylor-Polynom k- ter Ordnung von f bei 0 und sein Restterm in der Lagrange-Form gegeben durch

${\displaystyle P_{k}(x)=1+x+{\frac {x^{2}}{2!}}+\cdots +{\frac {x^{k}}{k!}},\ qquad R_{k}(x)={\frac {e^{\xi}}{(k+1)!}}x^{k+1},}$

wobei ξ eine Zahl zwischen 0 und x ist . Da e ^x um ( ⁎ ) wächst , können wir einfach e ^x  ≤ 1 für x  ∈ [−1, 0] verwenden, um den Rest auf dem Teilintervall [−1, 0] abzuschätzen. Um eine obere Schranke für den Rest auf [0,1] zu erhalten, verwenden wir die Eigenschaft e ^ξ < e ^x für 0< ξ < x, um abzuschätzen

${\displaystyle e^{x}=1+x+{\frac {e^{\xi}}{2}}x^{2}<1+x+{\frac {e^{x}}{2}} x^{2},\qquad 0<x\leq 1}$

unter Verwendung der Taylor-Entwicklung zweiter Ordnung. Dann lösen wir nach e ^x auf, um abzuleiten, dass

${\displaystyle e^{x}\leq {\frac {1+x}{1-{\frac {x^{2}}{2}}}}}=2{\frac {1+x}{2- x^{2}}}\leq 4,\qquad 0\leq x\leq 1}$

indem man einfach den Zähler maximiert und den Nenner minimiert . Wenn wir diese Schätzungen für e ^x kombinieren, sehen wir, dass

${\displaystyle |R_{k}(x)|\leq {\frac {4|x|^{k+1}}{(k+1)!}}\leq {\frac {4}{(k+ .) 1)!}},\qquad -1\leq x\leq 1,}$

die erforderliche Präzision ist also sicher erreicht, wenn

${\displaystyle {\frac {4}{(k+1)!}}<10^{-5}\quad \Longleftrightarrow \quad 4\cdot 10^{5}<(k+1)!\quad \Longleftrightarrow \quadk\geq 9.}$

(Siehe Fakultät oder berechne von Hand die Werte 9! =362 880 und 10! =3 628 800 .) Zusammenfassend führt der Satz von Taylor zur Approximation

${\displaystyle e^{x}=1+x+{\frac {x^{2}}{2!}}+\cdots +{\frac {x^{9}}{9!}}+R_{9 }(x),\qquad |R_{9}(x)|<10^{-5},\qquad -1\leq x\leq 1.}$

Diese Näherung liefert beispielsweise einen dezimalen Ausdruck e  2,71828, der bis zu fünf Dezimalstellen korrigiert.

Beziehung zur Analytik

Taylorentwicklungen reeller analytischer Funktionen

Sei I ⊂ R ein offenes Intervall . Per Definition ist eine Funktion f  : I → R ist reell analytische wenn es lokal durch eine konvergente definiert ist Potenzreihe . Dies bedeutet , dass für jeden a  ∈  I gibt es einige existiert r  > 0 und eine Folge von Koeffizienten c _k  ∈  R , so daß ( ein - r , a + r ) ⊂ I und

${\displaystyle f(x)=\sum_{k=0}^{\infty}c_{k}(xa)^{k}=c_{0}+c_{1}(xa)+c_{2} (xa)^{2}+\cdots ,\qquad |xa|<r.}$

Im Allgemeinen lässt sich der Konvergenzradius einer Potenzreihe aus der Cauchy-Hadamard-Formel berechnen

${\displaystyle {\frac{1}{R}}=\limsup_{k\to\infty}|c_{k}|^{\frac{1}{k}}.}$

Dieses Ergebnis basiert auf dem Vergleich mit einer geometrischen Reihe , und die gleiche Methode zeigt, dass, wenn die Potenzreihe basierend auf a für ein b ∈ R konvergiert, sie gleichmäßig auf dem geschlossenen Intervall [ a − r _b , a + r _b ] konvergieren muss. , wobei r _b  = | b  −  a |. Hier wird nur die Konvergenz der Potenzreihen betrachtet, und es könnte durchaus sein, dass ( a − R , a + R ) über den Bereich I von f hinausreicht .

Die Taylor-Polynome der reellen analytischen Funktion f an a sind einfach die endlichen Verkürzungen

${\displaystyle P_{k}(x)=\sum_{j=0}^{k}c_{j}(xa)^{j},\qquad c_{j}={\frac {f^{( j)}(a)}{j!}}}$

seiner lokal definierenden Potenzreihen, und die entsprechenden Restterme sind lokal durch die analytischen Funktionen

${\displaystyle R_{k}(x)=\sum_{j=k+1}^{\infty}c_{j}(xa)^{j}=(xa)^{k}h_{k}( x),\qquad |xa|<r.}$

Hier die Funktionen

${\displaystyle {\begin{ausgerichtet}&h_{k}:(ar,a+r)\to \mathbb {R} \\&h_{k}(x)=(xa)\sum _{j=0}^ {\infty}c_{k+1+j}\left(xa\right)^{j}\end{ausgerichtet}}}$

sind auch analytisch, da ihre definierenden Potenzreihen denselben Konvergenzradius wie die ursprüngliche Reihe haben. Unter der Annahme , dass [ ein - r , a + r ] ⊂ I und r  <  R , all diese Reihen konvergieren gleichmäßig auf ( ein - r , a + r ) . Natürlich kann man bei analytischen Funktionen den Restterm R _k ( x ) durch den Schwanz der Folge der Ableitungen f′ ( a ) im Zentrum der Entwicklung abschätzen , aber bei der komplexen Analysis ergibt sich auch eine andere Möglichkeit, die wird unten beschrieben .

Satz von Taylor und Konvergenz von Taylorreihen

Die Taylor-Reihe von f wird in einem Intervall konvergieren, in dem alle ihre Ableitungen beschränkt sind und nicht zu schnell wachsen, wenn k gegen Unendlich geht. (Jedoch, auch wenn die Reihe konvergiert Taylor, könnte es nicht konvergieren zu f , wie unten erläutert; f wird dann dem nicht sein analytisch .)

Man könnte an die Taylor-Reihe denken

${\displaystyle f(x)\approx \sum_{k=0}^{\infty}c_{k}(xa)^{k}=c_{0}+c_{1}(xa)+c_{2 }(xa)^{2}+\cdots}$

einer unendlich oft differenzierbaren Funktion f  : R → R als ihr "Taylor-Polynom unendlicher Ordnung" an a . Nun implizieren die Abschätzungen für den Rest , dass wenn für jedes r die Ableitungen von f als beschränkt über ( a  −  r , a  +  r ) bekannt sind, dann für jede Ordnung k und für jedes r  > 0 eine Konstante M . existiert _k,r > 0 so dass

${\displaystyle |R_{k}(x)|\leq M_{k,r}{\frac {|xa|^{k+1}}{(k+1)!}}}$

( ⁎⁎ )

für jedes x  ∈ ( a  −  r , a  +  r ). Manchmal können die Konstanten M _k,r so gewählt werden, dass M _k,r für festes r und alle k nach oben beschränkt ist . Dann konvergiert die Taylorreihe von f gleichmäßig gegen eine analytische Funktion

${\displaystyle {\begin{ausgerichtet}&T_{f}:(ar,a+r)\to \mathbb {R} \\&T_{f}(x)=\sum _{k=0}^{\infty }{\frac {f^{(k)}(a)}{k!}}\left(xa\right)^{k}\end{ausgerichtet}}}$

(Man erhält auch dann Konvergenz, wenn M _k,r nicht nach oben beschränkt ist, solange es langsam genug wächst.)

Die Grenzfunktion T _f ist per Definition immer analytisch, aber sie ist nicht notwendigerweise gleich der ursprünglichen Funktion f , auch wenn f unendlich differenzierbar ist. In diesem Fall sagen wir, dass f eine nichtanalytische glatte Funktion ist , zum Beispiel eine flache Funktion :

${\displaystyle {\begin{ausgerichtet}&f:\mathbb {R} \to \mathbb {R} \\&f(x)={\begin{cases}e^{-{\frac {1}{x^{ 2}}}}&x>0\\0&x\leq 0.\end{Fälle}}\end{ausgerichtet}}}$

Unter Verwendung der Kettenregel wiederholt durch mathematische Induktion , zeigt man, dass für jede Bestellung  k ,

${\displaystyle f^{(k)}(x)={\begin{cases}{\frac {p_{k}(x)}{x^{3k}}}\cdot e^{-{\frac { 1}{x^{2}}}}&x>0\\0&x\leq 0\end{cases}}}$

für ein Polynom p _k vom Grad 2( k − 1). Die Funktion tendiert schneller gegen Null als jedes Polynom, da x → 0 , also ist f unendlich oft differenzierbar und f ^{( k )} (0) = 0 für jede positive ganze Zahl k . Die obigen Ergebnisse gelten in diesem Fall alle: ${\displaystyle e^{-{\frac {1}{x^{2}}}}}$

• Die Taylor-Reihe von f konvergiert gleichmäßig gegen die Nullfunktion T _f ( x ) = 0, die analytisch mit allen Koeffizienten gleich Null ist.
• Die Funktion f ist ungleich dieser Taylor-Reihe und daher nicht analytisch.
• Für jede Ordnung k  ∈  N und Radius r  > 0 existiert M _k,r  > 0, das die obige Restschranke ( ⁎⁎ ) erfüllt .

Wenn jedoch k für festes r ansteigt _, wächst der Wert von M _k,r schneller als r ^k , und der Fehler geht nicht auf Null .

Satz von Taylor in der komplexen Analysis

Der Satz von Taylor verallgemeinert auf Funktionen f  : C → C, die in einer offenen Teilmenge U  ⊂  C der komplexen Ebene komplex differenzierbar sind . Seine Nützlichkeit wird jedoch von anderen allgemeinen Sätzen in der komplexen Analysis in den Schatten gestellt . Nämlich können stärkere Versionen verwandter Ergebnisse für komplexe differenzierbare Funktionen f  :  U  →  C abgeleitet werden, indem die Integralformel von Cauchy wie folgt verwendet wird.

Sei r  > 0, so dass die geschlossene Scheibe B ( z ,  r ) ∪  S ( z ,  r ) in U enthalten ist . Dann Cauchy Integralformel mit einer positiven Parametrisierung γ ( t ) = z + re ^es des Kreis S ( z , r ) mit t ∈ [0, 2 π ] ergibt

${\displaystyle f(z)={\frac {1}{2\pi i}}\int _{\gamma }{\frac {f(w)}{wz}}\,dw,\quad f'( z)={\frac {1}{2\pi i}}\int _{\gamma }{\frac {f(w)}{(wz)^{2}}}\,dw,\quad \ldots ,\quad f^{(k)}(z)={\frac {k!}{2\pi i}}\int _{\gamma }{\frac {f(w)}{(wz)^{ k+1}}}\,dw.}$

Hier sind alle Integranden auf dem Kreis S ( z ,  r ) stetig , was eine Differentiation unter dem Integralzeichen rechtfertigt. Insbesondere wenn f einmal komplex differenzierbar auf der offenen Menge U ist , dann ist es tatsächlich unendlich oft komplex differenzierbar auf U . Man erhält auch die Schätzungen von Cauchy

${\displaystyle |f^{(k)}(z)|\leq {\frac {k!}{2\pi}}\int _{\gamma }{\frac {M_{r}}{|wz| ^{k+1}}}\,dw={\frac {k!M_{r}}{r^{k}}},\quad M_{r}=\max _{|wc|=r}| f(w)|}$

für jedes z  ∈  U und r  > 0 , so dass B ( z ,  r ) ∪  S ( c ,  r ) ⊂  U . Diese Abschätzungen implizieren, dass die komplexe Taylorreihe

${\displaystyle T_{f}(z)=\sum_{k=0}^{\infty }{\frac {f^{(k)}(c)}{k!}}(zc)^{k }}$

von f konvergiert gleichmäßig auf jeder offenen Scheibe B ( c ,  r )  U mit S ( c ,  r )  U in eine Funktion T _f . Mit den Konturintegralformeln für die Ableitungen f ^{( k )} ( c )

${\displaystyle {\begin{ausgerichtet}T_{f}(z)&=\sum_{k=0}^{\infty }{\frac {(zc)^{k}}{2\pi i}} \int _{\gamma }{\frac {f(w)}{(wc)^{k+1}}}\,dw\\&={\frac {1}{2\pi i}}\int _{\gamma}{\frac{f(w)}{wc}}\sum_{k=0}^{\infty}\left({\frac{zc}{wc}}\right)^{k }\,dw\\&={\frac {1}{2\pi i}}\int _{\gamma }{\frac {f(w)}{wc}}\left({\frac {1} {1-{\frac {zc}{wc}}}}\right)\,dw\\&={\frac {1}{2\pi i}}\int _{\gamma }{\frac {f (w)}{wz}}\,dw=f(z),\end{ausgerichtet}}}$

also ist jede komplexe differenzierbare Funktion f in einer offenen Menge U  ⊂  C tatsächlich komplex analytisch . Alles, was hier für reelle analytische Funktionen gesagt wurde, gilt hier auch für komplexe analytische Funktionen, wobei das offene Intervall I durch eine offene Teilmenge U  ∈  C und a- zentrierte Intervalle ( a  −  r ,  a  +  r ) ersetzt durch c- zentrierte Scheiben B ( c ,  r ). Insbesondere gilt die Taylorentwicklung in der Form

${\displaystyle f(z)=P_{k}(z)+R_{k}(z),\quad P_{k}(z)=\sum_{j=0}^{k}{\frac { f^{(j)}(c)}{j!}}(zc)^{j},}$

wobei der Restterm R _{k komplexanalytisch} ist. Methoden der komplexen Analysis liefern einige aussagekräftige Ergebnisse bezüglich Taylor-Entwicklungen. Verwendet man beispielsweise Cauchys Integralformel für jede positiv orientierte Jordan-Kurve γ, die den Rand ∂ W  ⊂  U einer Region W  ⊂  U parametrisiert , erhält man Ausdrücke für die Ableitungen f ^{( j )} ( c ) wie oben und modifiziert die Berechnung leicht für T _f ( z ) = f ( z ) erhält man die exakte Formel

${\displaystyle R_{k}(z)=\sum _{j=k+1}^{\infty }{\frac {(zc)^{j}}{2\pi i}}\int _{\ gamma }{\frac {f(w)}{(wc)^{j+1}}}\,dw={\frac {(zc)^{k+1}}{2\pi i}}\int _{\gamma}{\frac{f(w)\,dw}{(wc)^{k+1}(wz)}},\qquad z\in W.}$

Wichtig ist hier , dass die Qualität der Approximation durch eine Taylor - Polynom auf dem Gebiet W  ⊂  U durch die Werte der Funktion beherrscht f sich auf die Grenze ∂ W  ⊂  U . In ähnlicher Weise erhält man, wenn man Cauchys Schätzungen auf den Reihenausdruck für den Rest anwendet, die einheitlichen Schätzungen

${\displaystyle |R_{k}(z)|\leq \sum_{j=k+1}^{\infty }{\frac {M_{r}|zc|^{j}}{r^{j }}}={\frac {M_{r}}{r^{k+1}}}{\frac {|zc|^{k+1}}{1-{\frac {|zc|}{r }}}}\leq {\frac {M_{r}\beta ^{k+1}}{1-\beta}},\qquad {\frac {|zc|}{r}}\leq \beta < 1.}$

Beispiel

Komplexes Diagramm von f ( z ) = 1/(1 +  z ² ). Der Modul wird durch Elevation und Argument durch Farbgebung angezeigt: Cyan=0, Blau =  π /3, Violett = 2 π /3, Rot =  π , Gelb=4 π /3, Grün=5 π /3.

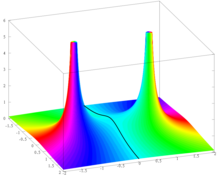
Die Funktion

${\displaystyle {\begin{aligned}&f:\mathbb {R} \to \mathbb {R} \\&f(x)={\frac {1}{1+x^{2}}}\end{aligned }}}$

ist reell analytisch , d. h. lokal durch seine Taylor-Reihe bestimmt. Diese Funktion wurde oben aufgetragen, um zu verdeutlichen, dass einige elementare Funktionen in zu großen Umgebungen des Expansionszentrums nicht durch Taylor-Polynome approximiert werden können. Dieses Verhalten ist im Rahmen komplexer Analysen leicht zu verstehen. Die Funktion f erweitert sich nämlich in eine meromorphe Funktion

${\displaystyle {\begin{ausgerichtet}&f:\mathbb {C} \cup \{\infty\}\to \mathbb {C} \cup \{\infty\}\\&f(z)={\frac { 1}{1+z^{2}}}\end{ausgerichtet}}}$

auf der kompaktifizierten komplexen Ebene. Es hat einfache Pole bei z  =  i und z  = − i , und es ist an anderer Stelle analytisch. Nun konvergiert ihre bei z ₀ zentrierte Taylorreihe auf einer beliebigen Scheibe B ( z ₀ , r ) mit r < | z  −  z ₀ |, wobei die gleiche Taylorreihe bei z  ∈  C konvergiert . Daher Taylor Reihe von f zentriert bei 0 konvergiert auf B (0, 1) und sie konvergiert nicht für z ∈ C mit | z | > 1 wegen der Pole bei i und − i . Aus dem gleichen Grund die Taylor - Reihe von f zentriert bei 1 konvergiert auf B (1, √2) und konvergiert nicht für z  ∈  C mit | z  − 1| > 2.

Verallgemeinerungen des Satzes von Taylor

Differenzierbarkeit höherer Ordnung

Eine Funktion f : R ⁿ  →  R ist bei a  ∈  R ⁿ genau dann differenzierbar, wenn es ein lineares Funktional L  :  R ⁿ  →  R und eine Funktion h  :  R ⁿ  →  R gibt mit

${\displaystyle f({\boldsymbol {x}})=f({\boldsymbol {a}})+L({\boldsymbol {x}}-{\boldsymbol {a}})+h({\boldsymbol { x}})\lVert {\boldsymbol {x}}-{\boldsymbol {a}}\rVert ,\qquad \lim _{{\boldsymbol {x}}\to {\boldsymbol {a}}}h({ \boldsymbol{x}})=0.}$

Ist dies der Fall, so ist L  =  df ( a ) das (eindeutig definierte) Differential von f im Punkt a . Außerdem existieren dann die partiellen Ableitungen von f an a und das Differential von f an a ist gegeben durch

${\displaystyle df({\boldsymbol {a}})({\boldsymbol {v}})={\frac {\partial f}{\partial x_{1}}}({\boldsymbol {a}})v_ {1}+\cdots +{\frac{\partial f}{\partial x_{n}}}({\boldsymbol{a}})v_{n}.}$

Einführung der Multi-Index-Notation

${\displaystyle |\alpha |=\alpha_{1}+\cdots +\alpha_{n},\quad\alpha!=\alpha_{1}!\cdots\alpha_{n}!,\quad {\boldsymbol {x}}^{\alpha}=x_{1}^{\alpha_{1}}\cdots x_{n}^{\alpha_{n}}}$

für & agr;  ∈  N ⁿ und x  ∈  R ⁿ . Wenn alle partiellen Ableitungen k- ter Ordnung von f  : R ⁿ → R bei a ∈ R ⁿ stetig sind , dann kann man nach dem Satz von Clairaut die Ordnung der gemischten Ableitungen bei a ändern , also die Notation

${\displaystyle D^{\alpha}f={\frac {\partial^{|\alpha |}f}{\partial x_{1}^{\alpha_{1}}\cdots\partial x_{n} ^{\alpha_{n}}}},\qquad |\alpha |\leq k}$

für die partiellen Ableitungen höherer Ordnung ist in dieser Situation gerechtfertigt. Das gleiche gilt, wenn alle  partiellen Ableitungen ( k − 1)-ter Ordnung von f in einer Umgebung von a existieren und an a differenzierbar sind . Dann sagen wir , dass f ist k - mal an dem Punkt differenzierbar  ein .

Satz von Taylor für multivariate Funktionen

Wenn die Funktion f  : R ⁿ → R ist k  + 1 mal stetig differenzierbar ist in einer geschlossenen Kugel für einen Teil , dann eine genaue Formel für den Rest in Form einer ableiten kann ( k + 1) -ter Ordnung partielle Ableitungen von f in diesem Nachbarschaft. Nämlich, ${\displaystyle B=\{\mathbf{y}\in\mathbb{R}^{n}:\left\|\mathbf{a} -\mathbf{y}\right\|\leq r\}}$${\displaystyle r>0}$

${\displaystyle {\begin{ausgerichtet}&f({\boldsymbol {x}})=\sum _{|\alpha |\leq k}{\frac {D^{\alpha}f({\boldsymbol {a} })}{\alpha!}}({\boldsymbol {x}}-{\boldsymbol {a}})^{\alpha}+\sum _{|\beta |=k+1}R_{\beta} ({\boldsymbol {x}})({\boldsymbol {x}}-{\boldsymbol {a}})^{\beta},\\&R_{\beta}({\boldsymbol {x}})={ \frac {|\beta |}{\beta !}}\int _{0}^{1}(1-t)^{|\beta |-1}D^{\beta}f{\big (} {\boldsymbol {a}}+t({\boldsymbol {x}}-{\boldsymbol {a}}){\big)}\,dt.\end{ausgerichtet}}}$

In diesem Fall erhält man wegen der Stetigkeit der partiellen Ableitungen ( k + 1)-ter Ordnung in der kompakten Menge B sofort die einheitlichen Abschätzungen

${\displaystyle \left|R_{\beta}({\boldsymbol {x}})\right|\leq {\frac {1}{\beta !}}\max _{|\alpha |=|\beta | }\max _{{\boldsymbol {y}}\in B}|D^{\alpha}f({\boldsymbol {y}})|,\qquad {\boldsymbol {x}}\in B.}$

Beispiel in zwei Dimensionen

Zum Beispiel ist das Taylor-Polynom dritter Ordnung einer glatten Funktion f : R ²  →  R mit x − a = v ,

${\displaystyle {\begin{ausgerichtet}P_{3}({\boldsymbol {x}})=f({\boldsymbol {a}})+{}&{\frac {\partial f}{\partial x_{ 1}}}({\boldsymbol {a}})v_{1}+{\frac {\partial f}{\partial x_{2}}}({\boldsymbol {a}})v_{2}+{ \frac {\partial^{2}f}{\partial x_{1}^{2}}}({\boldsymbol {a}}){\frac {v_{1}^{2}}{2!} }+{\frac{\partial^{2}f}{\partial x_{1}\partial x_{2}}}({\boldsymbol {a}})v_{1}v_{2}+{\frac {\partial ^{2}f}{\partial x_{2}^{2}}}({\boldsymbol {a}}){\frac {v_{2}^{2}}{2!}}\ \&+{\frac {\partial^{3}f}{\partial x_{1}^{3}}}({\boldsymbol {a}}){\frac {v_{1}^{3}} {3!}}+{\frac {\partial^{3}f}{\partial x_{1}^{2}\partial x_{2}}}}({\boldsymbol {a}}){\frac { v_{1}^{2}v_{2}}{2!}}+{\frac {\partial^{3}f}{\partial x_{1}\partial x_{2}^{2}}} ({\boldsymbol {a}}){\frac {v_{1}v_{2}^{2}}{2!}}+{\frac {\partial ^{3}f}{\partial x_{2 }^{3}}}({\boldsymbol {a}}){\frac {v_{2}^{3}}{3!}}\end{ausgerichtet}}}$

Beweise

Beweis für den Satz von Taylor in einer reellen Variablen

Lassen

${\displaystyle h_{k}(x)={\begin{cases}{\frac {f(x)-P(x)}{(xa)^{k}}}&x\not =a\\0&x= a\end{Fälle}}}$

wobei, wie in der Aussage des Satzes von Taylor,

${\displaystyle P(x)=f(a)+f'(a)(xa)+{\frac {f''(a)}{2!}}(xa)^{2}+\cdots +{ \frac {f^{(k)}(a)}{k!}}(xa)^{k}.}$

Es genügt zu zeigen, dass

${\displaystyle \lim_{x\to a}h_{k}(x)=0.}$

Der Beweis hier basiert auf der wiederholten Anwendung der Regel von L'Hôpital . Beachten Sie, dass für jedes j = 0,1,…, k −1 , . Daher verschwindet jede der ersten k −1 Ableitungen des Zählers in bei , und das gleiche gilt für den Nenner. Da auch die Bedingung , dass die Funktion f seiner k mal an einem Punkt differenzierbar Differenzierbarkeit erfordert bis zu Ordnung k -1 in einer Umgebung des Punktes (das ist wahr, weil Differenzierbarkeit eine Funktion erfordert in einer ganzen Umgebung eines Punktes zu definieren ), sind der Zähler und seine k  − 2 Ableitungen in einer Umgebung von a differenzierbar . Offensichtlich erfüllt auch der Nenner diese Bedingung und verschwindet zusätzlich nicht, es sei denn, x = a , daher sind alle für die L'Hopital-Regel notwendigen Bedingungen erfüllt und ihre Verwendung ist gerechtfertigt. So ${\displaystyle f^{(j)}(a)=P^{(j)}(a)}$${\displaystyle h_{k}(x)}$${\displaystyle x=a}$

${\displaystyle {\begin{ausgerichtet}\lim _{x\to a}{\frac {f(x)-P(x)}{(xa)^{k}}}&=\lim_{x\ nach a}{\frac {{\frac {d}{dx}}(f(x)-P(x))}{{\frac {d}{dx}}(xa)^{k}}}= \cdots =\lim_{x\to a}{\frac {{\frac {d^{k-1}}{dx^{k-1}}}(f(x)-P(x))} {{\frac {d^{k-1}}{dx^{k-1}}}(xa)^{k}}}\\&={\frac {1}{k!}}\lim_ {x\to a}{\frac {f^{(k-1)}(x)-P^{(k-1)}(x)}{xa}}\\&={\frac {1} {k!}}(f^{(k)}(a)-f^{(k)}(a))=0\end{ausgerichtet}}}$

wobei die letzte Gleichheit durch die Definition der Ableitung bei x  =  a folgt  .

Ableitung für die Mittelwertformen des Restes

Sei G eine beliebige reellwertige Funktion, stetig auf dem geschlossenen Intervall zwischen a und x und differenzierbar mit einer nicht verschwindenden Ableitung auf dem offenen Intervall zwischen a und x , und definiere

${\displaystyle F(t)=f(t)+f'(t)(xt)+{\frac {f''(t)}{2!}}(xt)^{2}+\cdots +{ \frac {f^{(k)}(t)}{k!}}(xt)^{k}.}$

Für . Dann wird durch Cauchys Mittelwertsatz , ${\displaystyle t\in [a,x]}$

${\displaystyle {\frac {F'(\xi)}{G'(\xi)}}={\frac {F(x)-F(a)}{G(x)-G(a)}} }$

( ⁎⁎⁎ )

für einige ξ auf dem offenen Intervall zwischen a und x . Beachten Sie, dass hier der Zähler F ( x ) − F ( a ) = R _k ( x ) genau der Rest des Taylor-Polynoms für f ( x ) ist. Berechnen

${\displaystyle {\begin{ausgerichtet}F'(t)={}&f'(t)+{\big (}f''(t)(xt)-f'(t){\big)}+\ links({\frac {f^{(3)}(t)}{2!}}(xt)^{2}-{\frac {f^{(2)}(t)}{1!}} (xt)\right)+\cdots \\&\cdots +\left({\frac {f^{(k+1)}(t)}{k!}}(xt)^{k}-{\ frac {f^{(k)}(t)}{(k-1)!}}(xt)^{k-1}\right)={\frac {f^{(k+1)}(t )}{k!}}(xt)^{k},\end{ausgerichtet}}}$

setze es in ( ⁎⁎⁎ ) ein und ordne die Begriffe neu an, um das zu finden

${\displaystyle R_{k}(x)={\frac {f^{(k+1)}(\xi)}{k!}}(x-\xi)^{k}{\frac {G( x)-G(a)}{G'(\xi)}}.}$

Dies ist die Form des Restterms, der nach der eigentlichen Aussage des Taylor-Theorems mit Rest in Mittelwertform genannt wird. Die Lagrange-Form des Rests findet man durch Auswählen und die Cauchy-Form durch Auswählen von . ${\displaystyle G(t)=(xt)^{k+1}}$${\displaystyle G(t)=ta}$

Anmerkung. Mit dieser Methode kann man auch die ganzzahlige Form des Restes wiederherstellen, indem man wählt

${\displaystyle G(t)=\int _{a}^{t}{\frac {f^{(k+1)}(s)}{k!}}(xs)^{k}\,ds ,}$

aber die für die Anwendung des Mittelwertsatzes erforderlichen Anforderungen an f sind zu hoch, wenn man die Behauptung beweisen will für den Fall, dass f ^{( k )} nur absolut stetig ist . Wenn man jedoch das Riemann-Integral anstelle des Lebesgue-Integrals verwendet , können die Annahmen nicht abgeschwächt werden.

Herleitung für die Integralform des Rests

Aufgrund der absoluten Stetigkeit von f ^{( k )} auf dem geschlossenen Intervall zwischen a und x existiert seine Ableitung f ^{( k + 1)} als L ¹ -Funktion, und wir können den Fundamentalsatz der Infinitesimalrechnung und der partiellen Integration verwenden . Das gleiche gilt für den Nachweis Riemann Integral unter der Annahme , dass f ^{( k )} ist kontinuierliches auf dem abgeschlossenen Intervall und differenzierbar auf dem offenen Intervall zwischen a und x , und dies führt zu dem gleichen Ergebnis , als den Mittelwertsatz verwenden.

Der fundamentale Satz der Infinitesimalrechnung besagt, dass

${\displaystyle f(x)=f(a)+\int _{a}^{x}\,f'(t)\,dt.}$

Jetzt können wir nach Teilen integrieren und wieder den Fundamentalsatz der Infinitesimalrechnung verwenden, um das zu sehen

${\displaystyle {\begin{ausgerichtet}f(x)&=f(a)+{\Big (}xf'(x)-af'(a){\Big )}-\int _{a}^{ x}tf''(t)\,dt\\&=f(a)+x\left(f'(a)+\int _{a}^{x}f''(t)\,dt\ rechts)-af'(a)-\int _{a}^{x}tf''(t)\,dt\\&=f(a)+(xa)f'(a)+\int _{ a}^{x}\,(xt)f''(t)\,dt,\end{ausgerichtet}}}$

was genau der Satz von Taylor mit Rest in ganzzahliger Form im Fall k = 1 ist. Die allgemeine Aussage wird mit Induktion bewiesen . Nehme an, dass

${\displaystyle f(x)=f(a)+{\frac {f'(a)}{1!}}(xa)+\cdots +{\frac {f^{(k)}(a)} {k!}}(xa)^{k}+\int_{a}^{x}{\frac {f^{(k+1)}(t)}{k!}}(xt)^{ k}\,dt.}$

( ⁎⁎⁎⁎ )

Integrieren des Restterms durch Teile erhalten wir

${\displaystyle {\begin{ausgerichtet}\int _{a}^{x}{\frac {f^{(k+1)}(t)}{k!}}(xt)^{k}\, dt=&-\left[{\frac {f^{(k+1)}(t)}{(k+1)k!}}(xt)^{k+1}\right]_{a} ^{x}+\int_{a}^{x}{\frac {f^{(k+2)}(t)}{(k+1)k!}}(xt)^{k+1 }\,dt\\=&\ {\frac {f^{(k+1)}(a)}{(k+1)!}}(xa)^{k+1}+\int _{a }^{x}{\frac {f^{(k+2)}(t)}{(k+1)!}}(xt)^{k+1}\,dt.\end{ausgerichtet}} }$

Setzt man dies in die Formel in ( ⁎⁎⁎⁎ ) ein, so zeigt sich, dass, wenn es für den Wert k gilt , es auch für den Wert k  + 1 gelten muss. Da es also für k  = 1 gilt, muss es für jede positive ganze Zahl gelten  k .

Ableitung für den Rest multivariater Taylor-Polynome

Wir beweisen den Spezialfall, in dem f  : R ⁿ → R stetige partielle Ableitungen bis zur Ordnung k +1 in einer geschlossenen Kugel B mit Mittelpunkt a hat . Die Strategie des Beweises besteht darin, den Ein-Variablen-Fall des Satzes von Taylor auf die Beschränkung von f auf das an x und a angrenzende Geradensegment anzuwenden . Parametrieren Sie das Liniensegment zwischen a und x durch u ( t ) = a + t ( x − a ). Wir wenden die einvariable Version des Satzes von Taylor auf die Funktion g ( t ) = f ( u ( t )) an :

${\displaystyle f(\mathbf {x} )=g(1)=g(0)+\sum_{j=1}^{k}{\frac {1}{j!}}g^{(j )}(0)\ +\ \int _{0}^{1}{\frac {(1-t)^{k}}{k!}}g^{(k+1)}(t)\ ,dt.}$

Die Anwendung der Kettenregel für mehrere Variablen ergibt

${\displaystyle {\begin{ausgerichtet}g^{(j)}(t)&={\frac {d^{j}}{dt^{j}}}f(u(t))={\frac {d^{j}}{dt^{j}}}f(\mathbf{a} +t(\mathbf{x} -\mathbf{a}))\\&=\sum _{|\alpha | =j}\left({\begin{matrix}j\\\alpha \end{matrix}}\right)(D^{\alpha}f)(\mathbf {a} +t(\mathbf {x} - \mathbf{a}))(\mathbf{x} -\mathbf{a})^{\alpha}\end{ausgerichtet}}}$

wo ist der Multinomialkoeffizient . Da erhalten wir: ${\displaystyle {\tbinom {j}{\alpha}}}$${\displaystyle {\tfrac {1}{j!}}{\tbinom {j}{\alpha}}={\tfrac {1}{\alpha!}}}$

${\displaystyle f(\mathbf{x})=f(\mathbf{a})+\sum _{1\leq |\alpha |\leq k}{\frac {1}{\alpha!}}(D ^{\alpha}f)(\mathbf{a})(\mathbf{x} -\mathbf{a})^{\alpha}+\sum _{|\alpha |=k+1}{\frac{ k+1}{\alpha!}}(\mathbf{x} -\mathbf{a})^{\alpha}\int _{0}^{1}(1-t)^{k}(D^ {\alpha}f)(\mathbf{a} +t(\mathbf{x} -\mathbf{a}))\,dt.}$

Siehe auch

• Hadamards Lemma
• Laurent-Reihe  – Verallgemeinerte Potenzreihen, um negative Potenzen zuzulassen
• Padé-Approximant  – 'Beste' Approximation einer Funktion durch eine rationale Funktion gegebener Ordnung
• Newton-Serie

Fußnoten

Verweise

• Apostol, Tom (1967), Infinitesimalrechnung , Wiley, ISBN 0-471-00005-1.
• Apostol, Tom (1974), Mathematische Analyse , Addison-Wesley.
• Bartle, Robert G.; Sherbert, Donald R. (2011), Einführung in die Realanalyse (4. Aufl.), Wiley, ISBN 978-0-471-43331-6.
• Hörmander, L. (1976), Lineare partielle Differentialoperatoren, Band 1 , Springer, ISBN 978-3-540-00662-6.
• Kline, Morris (1972), Mathematisches Denken von der Antike bis zur Neuzeit, Band 2 , Oxford University Press.
• Kline, Morris (1998), Infinitesimalrechnung: Ein intuitiver und physikalischer Ansatz , Dover, ISBN 0-486-40453-6.
• Pedrick, George (1994), Ein erster Kurs in Analysis , Springer, ISBN 0-387-94108-8.
• Stromberg, Karl (1981), Einführung in die klassische reelle Analysis , Wadsworth, ISBN 978-0-534-98012-2.
• Rudin, Walter (1987), Real and Complex Analysis (3. Aufl.), McGraw-Hill, ISBN 0-07-054234-1.
• Tao, Terence (2014), Analyse, Band I (3. Aufl.), Hindustan Book Agency, ISBN 978-93-80250-64-9.